6A Задача о распределении ресурсов (вариант а)

Распределение мест в самолете

Неформальное описание задачи.

Пусть авиакомпания продает билеты на плановый рейс самолета. Имеющиеся места в самолете разделяются на места первого или места второго класса. Стоимость мест второго класса существенно ниже стоимости мест первого класса, и следовательно спрос на места первого класса также выше. Распределение мест на места первого и второго классов осуществляется до момента начала продажи билетов и в дальнейшем скорректировано быть не может. Также предполагается, что никто из пассажиров купленные на рейс билеты не сдает. Доход авиакомпании определяется стоимостью проданных билетов. В случае, если авиакомпания принимает решение выделить мест под первый класс меньше, чем спрос на первый класс, то авиакомпания не получит части дохода, который определяется количеством пассажиров, которым не хватило билетов на места первого класса. В случае, если авиакомпания принимает решение выделить мест под первый класс больше, чем спрос на места первого класса, то часть билетов останутся не проданными и авиакомпания понесет убытки. Задача сводится к выбору соотношения между местами первого и второго классов, при котором авиакомпания получит максимальный доход от продажи билетов.

Формальная постановка задачи.

Множество решений , где - решение выделить мест под места II класса, M – общее количество мест в самолете. Тогда под места I класса выделено ( ) мест. Стоимость билетов на места I класса равна , стоимость билетов на места II класса составляет . Покупательский спрос на места II класса описывается непрерывной случайной величиной X, принимающей значения из множества , где - спрос на мест второго класса. Случайная величина X описывается плотностью распределения на интервале . Покупательский спрос на места I класса описывается непрерывной случайной величиной Y, принимающей значения из множества , где - спрос на мест первого класса. Случайная величина Y описывается плотностью распределения на интервале . , - представляют собой независимые случайные величины.

Множество исходов (альтернатив) определяется принятым авиакомпанией решением о распределении мест между I и II классами и наблюдаемым спросом на билеты. Возможные значения функции ценности альтернатив показаны в таблице:

.

Диаграмма влияния

Диаграмма влияния для рассматриваемой задачи имеет вид

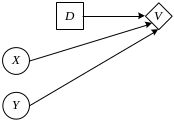
Расчет полезностей решений

Полезность некоторого решения равна:

.

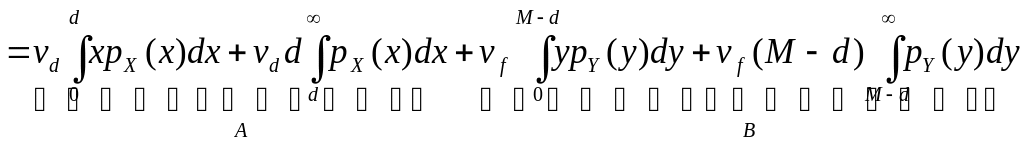Вычислим компоненту A:

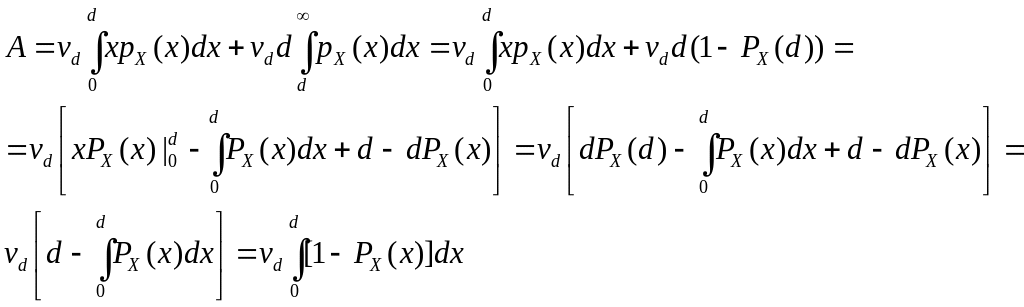
Аналогично для компоненты B:

,

тогда

Выбор решения

Байесовский подход к выбору решения. Для нахождения байесовского решения вычислим максимум функции полезности:

, тогда функция полезности достигает максимума, в случае, если выполняется равенство:

.

Графическое решение показано на рисунке ниже.

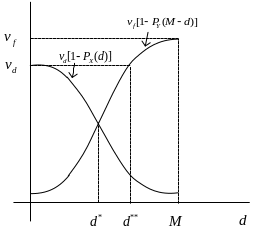
Полезность точной информации

Вариант1. Пусть имеется возможность узнать спрос на билеты во II классе, то есть значение случайной величины X.

Диаграмма влияния

Диаграмма влияния для рассматриваемой задачи имеет вид

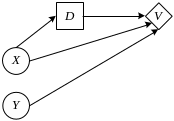
Тогда, если решение d принимается при наличии информации о спросе на места во II классе, то полезность решения равна:

Тогда байесовское решение определяется исходя из соотношения:

, откуда

.

Графическое решение показано на рисунке ниже.

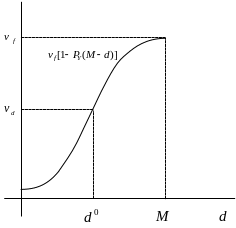
Байесовское решение при наличии точной информации о случайной величине X равно:

,

Полезность решения равна:

Вариант2. Пусть имеется возможность узнать спрос на билеты в I классе, то есть значение случайной величины Y.

Тогда байесовское решение при наличии точной информации о спросе на билеты первого класса:

Полезность решения равна:

.
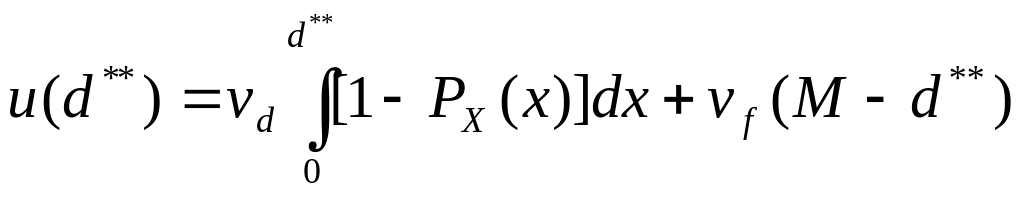