5В. Задача об управлении запасами

с ограниченным сроком хранения (вариант в)

Задача о молоке

Неформальное описание задачи.

Пусть предприятие занимается продажей молока. С округи скупаются запасы у фермеров, которые затем хранятся в цистерне. На следующий день молоко продается конечным покупателям. Если за день предприятию не удается продать молоко, то оно портится. Возможности использовать испорченное молоко у предприятия нет. Доход предприятия определяется количеством проданного молока и разницей между его оптовой и розничной стоимостью. В случае, если предприятие закупает недостаточно молока, и спрос на молоко превышает имеющееся количество молока, то предприятие не получит части дохода, который могло бы получить, закупив большее молока. В случае, если предприятие закупает слишком много молока, и часть молока остается не проданными, предприятие несет потери, равные оптовой стоимости не проданного молока. Задача сводится к выбору количества молока, закупка и продажа которого принесет предприятию наибольший доход.

Формальная постановка задачи.

Множество решений , где - решение закупить литров молока по оптовой цене . Покупательский спрос на молоко описывается непрерывной случайной величиной Y принимающей значения из множества , где - спрос на литров молока по розничной цене . Случайная величина Y описывается плотностью распределения на интервале .

Множество исходов (альтернатив) определяется принятым на предприятии решением и наблюдаемым на молоко спросом. Каждому из возможных исходов из множества поставим в соответствие ценность исхода (альтернативы), которая определяется как:

.

Диаграмма влияния

Диаграмма влияния для рассматриваемой задачи имеет вид

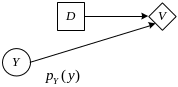
Расчет полезностей решений

Полезность некоторого решения равна:

, где

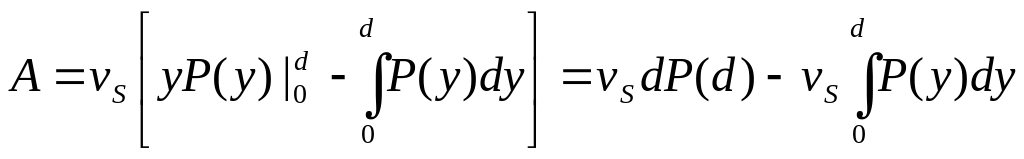
, с учетом того, что , получаем .

В качестве альтернативного варианта расчета полезности решения рассмотрим вариант, аналогичный тому, который был использован для дискретного случая.

.

Покажем, что .

Действительно, , так как для непрерывного распределения справедливо .

Таким образом, .

Выбор решения

Байесовский подход к выбору решения. Байесовский подход предполагает выбор решения , при котором .

Графическое решение показано на рисунке ниже.

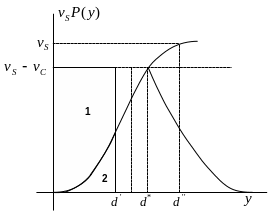
На рисунке цифрой “1” обозначена область равная , а цифрой “2” – область равная .

Из графика видно, что в случае, когда

, откуда

, тогда

.

Аналогичный результат можно получить, с использованием следующего соотношения:

, откуда

.

Полезность байесовского решения равна:

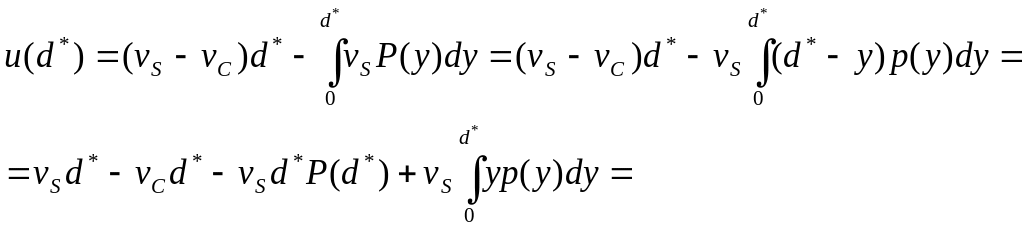
, где

- плотность распределения вероятности при условии, что спрос не превысит .

На рисунке показана условная плотность распределения случайной величины.

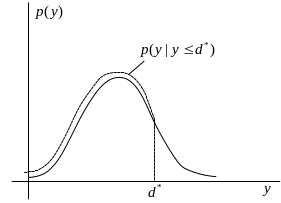
Полезность точной информации

Пусть у предприятия есть возможность получить точную оценку покупательского спроса на молоко. Требуется определить полезность наличия точной оценки.

Полезность решения , принимаемой в условиях, когда точно известно количество молока , которое будет куплено, равна:

.

Полезность точной информации для байесовского подхода:

Полезность точной информации для осторожного подхода:

Осторожным решением является решение не закупать молока: , соответственно полезность осторожного решения . Тогда .

Маржинальный анализ(Marginal analysis)

Рассмотрим дерево решений для задачи управления запасами. Пусть с использованием дерева решений требуется выбрать между закупкой и литров молока. Доход от решения о закупке литров оценивается относительно дохода, получаемой при решении о закупке литров молока, т.е. рассматривается изменение дохода . Решение о закупке литров молока называется базой сравнения, ценность решения принимается равным нулю.

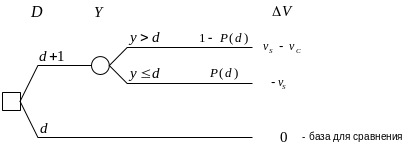
Изменение полезности от решения по отношению к полезности решения равно:

.

На рисунках ниже показано поведение функции полезности и изменение функции полезности.

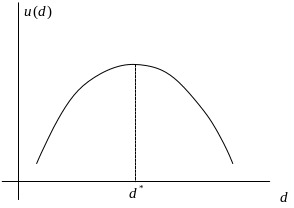
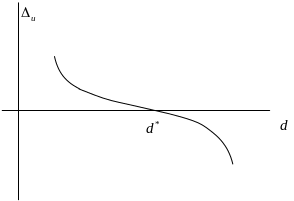
Приравнивая к нулю, получаем оптимальное с точки зрения байесовского подхода решение : .

Тогда , откуда

.

Задачи принятия решений о распределении ресурсов