5А. Задача об управлении запасами

с ограниченным сроком хранения (вариант а)

Задача о батареях

Задача о товарах с ограниченным сроком годности

Неформальная постановка задачи

Оптовый поставщик дорогих промышленных батарей специального назначения может продать до 3 шт. в год. Стоимость производства одной батареи составляет . Отпускная цена каждой батареи - и срок годности каждой – 1 год. Все непроданные батареи, пролежавшие год – ничего не стоят (стоимость просроченных батарей незначительна по сравнению со стоимостью производства). Спрос на батареи предсказать невозможно, но он, в любом случае, не больше 3 шт. в год. Необходимо принять решение, сколько батарей стоит выпустить в начале года, чтобы максимизировать ожидаемую годовую прибыль.

Формальная постановка задачи

Множество решений D , где – решение выпустить i батарей ( ). Случайная величина Y описывает спрос на батареи, - спрос на i батарей ( ). Принятое решение описывается величиной D, принимающей значения из множества D. Вероятность события обозначим как , функция распределения случайной величины Y: .

Каждому из возможных исходов (таковых будет , т.к. n = 3) поставим в соответствие ценность исхода :

На рисунке ниже представлено дерево решений для рассматриваемой задачи.

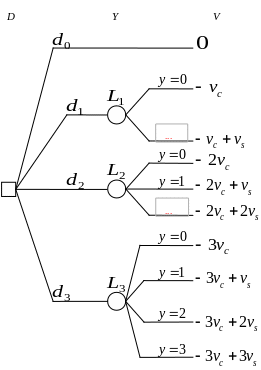
Диаграмма влияния

Диаграмма влияния для рассматриваемой задачи имеет вид :

Расчет полезностей решений

;

;

;

;

//Байесовское решение

5Б. Задача об управлении запасами

с ограниченным сроком хранения (вариант б)

Задача о газетах

Неформальное описание задачи.

Продавец газет ежедневно закупает газеты по оптовой цене, а затем продает их по розничной. Не проданные в течение дня газеты полностью теряют свою стоимость. Спрос на газеты определяется различными внешними факторами и не носит регулярного характера. Доход продавца определяется количеством проданных газет и разницей между оптовой и розничной стоимостью газет. В случае, если продавец закупает недостаточно газет, и спрос на газеты превышает имеющееся количество газет, то продавец не получит части дохода, которую мог бы получить, закупив большее число газет. В случае, если продавец закупает слишком много газет, и часть газет остается не проданными, продавец теряет на каждой непроданной газете ее оптовую стоимость. Задача сводится к выбору количества газет, закупка и продажа которых принесет продавцу наибольший доход.

Формальная постановка задачи.

Множество решений , где - решение закупить i штук газет по оптовой цене . Покупательский спрос на газеты описывается случайной величиной Y, принимающей значения из множества , где - наблюдается спрос на i штук газет по розничной цене . Вероятность события обозначим символом p_i:

, .

В зависимости от принятого торговцем решения и наблюдаемого спроса на газеты можно выделить исхода (альтернативы), входящие в множество исходов (альтернатив) .

Каждому из возможных исходов из множества поставим в соответствие ценность исхода (альтернативы), которая определяется как:

.

На рисунке ниже представлено дерево решений для рассматриваемой задачи.

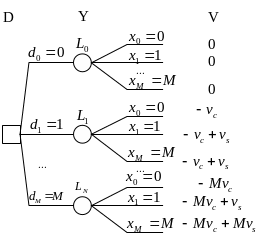
Диаграмма влияния

Диаграмма влияния для рассматриваемой задачи имеет вид

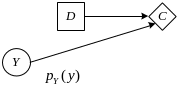
Расчет полезностей решений

Ценности исходов (альтернатив) определяются с учетом введенных обозначений как

.

Полезности решений , .. , соответственно равны:

;

;

;

;

…

.

В общем виде полезность решения D равна:

.

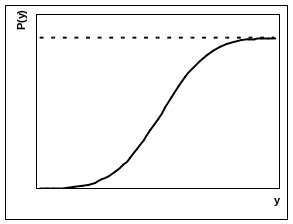
Покажем, что , где - функция распределения случайной величины . Графики плотности вероятности и функции распределения случайной величины показаны на рисунке ниже.

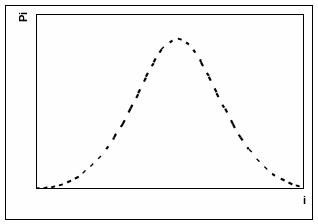
Рассмотрим доказательство утверждения по методу математической индукции.

1. База индукции. Докажем утверждение для .

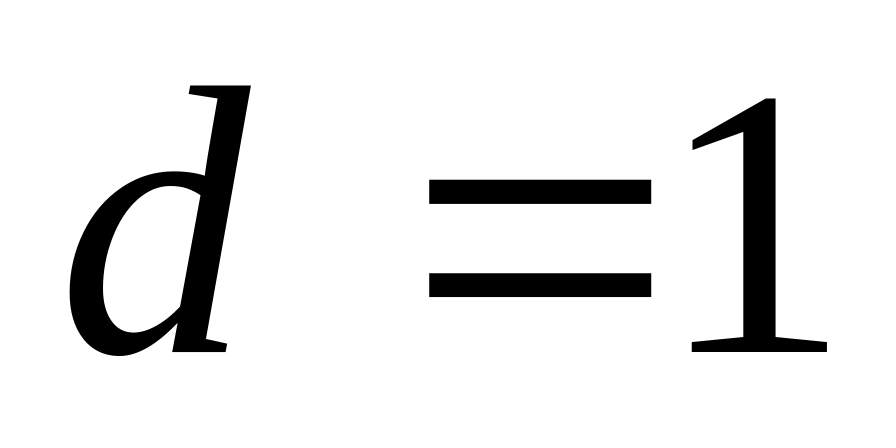Левая часть выражения равна: , правая часть выражения равна: , следовательно, при утверждение является верным.

2) Индукционный переход. Пусть утверждение справедливо при : ). Покажем, что в этом случае, утверждение справедливо и для : .

Действительно,

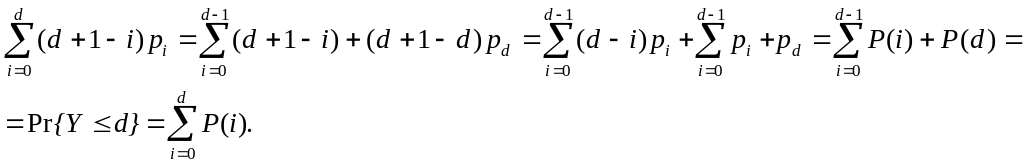
Итак, доказано что

.

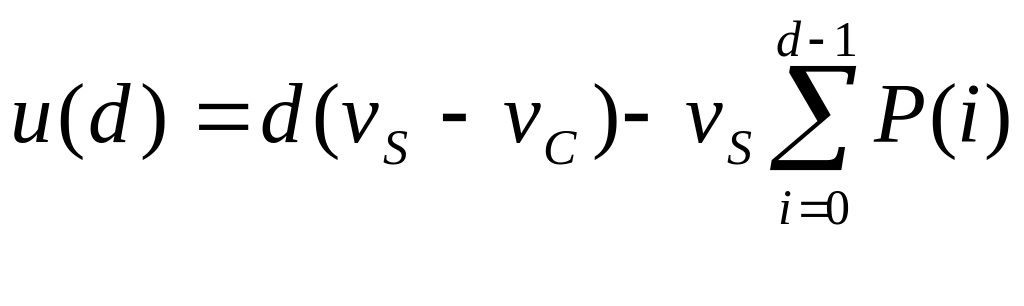Выбор решения

Байесовский подход к выбору решения. Байесовский подход предполагает выбор решения

. Для поиска максимума функции полезности сравниваем значения полезностей для решений , и . Рассмотрим разности полезностей соответствующих решений:

;

.

Тогда для байесовского решения справедливо:

,

.

Откуда ; .

Тогда в качестве приближенного решения рассмотрим:

.

Графическое решение задачи показано на рисунке ниже.

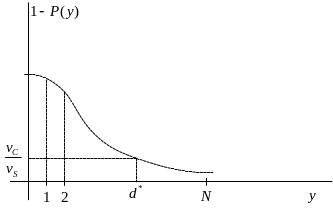
Если наценка составляет 100%, тогда , и, следовательно, - медиана функции распределения.

Дальнейший анализ задачи в такой постановке затруднителен и нужен переход к непрерывному случаю.