4. Задача об американском футболе (вариант а)
Неформальная постановка задачи
Пусть тренер со своей командой принимает участие в чемпионате по американскому футболу. В очень важной игре на чемпионате до конца матча остается меньше минуты, команда совершила тачдаун, при этом, проигрывает со счетом 16-17. По правилам, после тачдауна, команда может заработать дополнительные очки, тренеру предоставляется выбор: попробовать забить гол, заработав 1 очко и тем самым сравнять счет (при этом времени на победу уже не останется), либо попытаться совершить еще один тачдаун, заработав 2 очка и, возможно, выиграть матч. Будем считать, что вероятность забить гол гораздо выше, чем сделать еще один тачдаун.
Формальная постановка задачи
Множество решений , где – решение попробовать забить гол, – решение попытаться сделать тачдаун.
Случайная величина , принимает значение , если команда заработала дополнительные очки и , иначе. Принятое решение описывается величиной D, принимающей значения из множества D. Вероятность события в случае принятия решения будем обозначать как .
В зависимости от принятого решения и его результата, можно выделить четыре исхода (альтернативы), входящие во множество исходов (альтернатив) , где: - успешная попытка забить гол, - неуспешная попытка забить гол, - успешная попытка сделать тачдаун, - неуспешная попытка тачдауна.
Каждому из возможных исходов
,
поставим в соответствие
значение из множества результатов
,
которое определяет исход игры. Множество
результатов R={r1,r2,r3}={ничья,
поражение, победа}.
На рисунке ниже представлено дерево решений для рассматриваемой задачи.
В данной задаче множество лотерей состоит из двух элементов . На рисунке ниже лотереи приведены в развернутом виде с указанием вероятностей исходов.
Диаграммы влияния
Диаграмма влияния для рассматриваемой задачи имеет вид
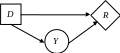
Расчет полезностей решений
Ценности исходов (альтернатив) определяются с учетом введенных обозначений как
;
;
.
Полезность решения (лотереи ) равна
.
Полезность решения (лотереи ) равна
.
Выбор решения
Байесовский подход. При наличии всего двух альтернатив, лучшее в байесовском смысле решение легко находится путем сравнения соответствующих полезностей:
. (1)
С учетом полученных значений полезности решений получаем:
,
после преобразований выражение имеет вид:
.
В рамках рассматриваемой задачи использование понятия «вероятность безразличия» является не корректным, в связи с тем, что принятое решение D оказывает влияние на распределение случайной величины Y.
4.Задача об американском футболе (вариант б)
Неформальная постановка задачи (1)
Два друга, Нэнси и Рон, наблюдающие за вышеописанным футбольным матчем, собираются заключить пари на исход матча после того, как тренер примет решение попытаться забить гол или же совершить еще один тачдаун. Нэнси предлагает следующие ставки Рону, и он соглашается:
Если тренер решится на попытку тачдауна, и его команда победит, Рон должен Нэнси $2. Если же не выиграют, тогда Нэнси платит Рону $1.
Если тренер принимает решение попробовать забить гол, и команда выигрывает, Рон платит Нэнси $0.25, если проигрывают, то Нэнси платит $1.
Нэнси может заключить пари, не зная решения тренера, либо сразу после того, как узнает, но до того, как исход матча будет известен. Рассмотрим последний случай.
Формальная постановка задачи (1)
Множество решений соответствует решению Нэнси, – решение делать ставку, – решение не делать ставку.
Случайная величина
,
где
- тренер принял решение попытаться
забить гол и
- тренер принял решение совершить
тачдаун, X
,
где
- команда победила и
- команда проиграла. Принятое решение
описывается величиной D,
принимающей значения из множества D.
Вероятность события
в случае принятия тренером решения
будем обозначать как
,
при этом
,
т.к. шанс заработать одно очко гораздо
выше, чем шанс заработать два очка.
В зависимости от принятого решения
Нэнси, тренера и его результата, можно
выделить шесть исходов (альтернатив),
входящих во множество исходов (альтернатив)
A
,
где:
- тренер принял решение попытаться
забить гол, Нэнси решила не делать
ставку,
- тренер принял решение попытаться
забить гол, Нэнси сделала ставку, команда
победила,
- тренер принял решение попытаться
забить гол, Нэнси сделала ставку, команда
проиграла,
- тренер принял решение совершить
тачдаун, Нэнси решила не делать ставку,
- тренер принял решение совершить
тачдаун, Нэнси сделала ставку, команда
победила,
- тренер принял решение совершить
тачдаун, Нэнси сделала ставку, команда
проиграла. Каждому из возможных
исходов
,
поставим в соответствие
ценность исхода (альтернативы)
.
На рисунке ниже представлено дерево
решений для рассматриваемой задачи.
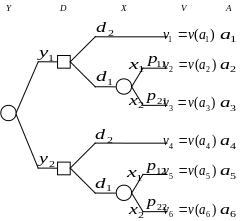
Диаграммы влияния (1)
Диаграмма влияния для рассматриваемой задачи имеет вид:
Расчет полезностей решений (1)
Ценности исходов (альтернатив) определяются с учетом введенных обозначений как
;
;
;
;
;
;
При
:
,
При
:
,
Нэнси считает, что
,
но поспорит с Роном, только если будет
уверена, что ее выигрыш будет
неотрицательным. Поскольку уже было
установлено значение выигрыша в том
или ином случае, она, вероятно полагает,
что:
и
,
или
и
.
Но Рон тоже согласился с условиями пари
и, чтобы выиграть, он должен считать,
что
и
.
Неформальная постановка задачи (2)
Предположим, что Нэнси полагает, что, если тренер решит попытаться забить гол, то команда выиграет с 90%-ой вероятностью, тогда как Рон считает, что эта вероятность - 75%. Таким образом, если тренер решит попытаться забить гол, то Нэнси и Рон заключат пари, потому что оба будут ожидать положительный доход, Нэнси 0.125 и Рон 0.0625. Однако, Нэнси предполагает, что и и для нее было бы предпочтительнее, чтобы тренер решился на попытку совершения тачдауна; обратное верно для Рона.
Рассмотрим задачу, когда Нэнси должна принять свое решение (заключать пари или нет), до того, как будет известно решение тренера.
Формальная постановка задачи (2)
Множество решений Нэнси
,
случайные величины
и X
,
остаются неизменными. Но в отличие от
предыдущего случая, теперь Нэнси должна
принять свое решение до того, как станет
известно решение тренера, поэтому она
должна оценить вероятность того, какое
решение примет тренер: попытаться забить
гол или попробовать совершить тачдаун.
Мы предполагаем, что ее решение будет
состоять в том, чтобы заключить пари
только в том случае, если ожидаемый
доход будет неотрицательным. Обозначим
- вероятность того, что тренер примет
решение попытаться забить гол. В
зависимости от принятого решения Нэнси,
тренера и его результата, выделим пять
исходов (альтернатив), входящих во
множество исходов (альтернатив) A
,
где:
- Нэнси заключила пари, тренер принял
решение попытаться забить гол, команда
выиграла,
- Нэнси заключился пари, тренер принял
решение попытаться забить гол, команда
проиграла,
- Нэнси заключился пари, тренер принял
решение попытаться совершить тачдаун,
команда выиграла,
- Нэнси заключился пари, тренер принял
решение попытаться совершить тачдаун,
команда проиграла,
- Нэнси решила не заключать пари.
Каждому из возможных исходов
,
поставим в соответствие
ценность исхода (альтернативы)
.
На рисунке ниже представлено дерево
решений для данного варианта рассматриваемой
задачи.
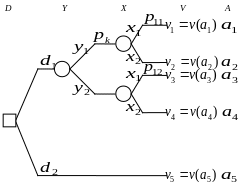
Диаграммы влияния (2)
Отметим два важных различия между данной и предыдущей диаграммой влияния. Во-первых, узел D – решение Нэнси, для наглядности изображен левее случайной величины Y – решение тренера, т.к. теперь Нэнси должна принять свое решение до принятия решения тренером. Во-вторых, исчезла дуга между D и Y, поскольку теперь решение тренера не влияет на решение Нэнси.
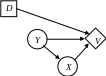
Расчет полезностей решений (2)
Ценности исходов (альтернатив) определяются с учетом введенных обозначений как
;
;
;
;
;
Полезность решения равна
.
Полезность решения равна
.
Выбор решения
Нэнси сделает ставку только в том случае,
если
и, конечно, ее решение будет зависеть
от вероятностей
,
и
.
.
С учетом полученных значений полезности решения:
.
Вероятность безразличия
– значение вероятности
,
при котором принятое решение не оказывает
влияния на математическое ожидание
получаемого дохода:
,
откуда вероятность безразличия равна:
.
Тогда:
Полезность точной информации
Выполним сравнение значений ожидаемых доходов для некоторых заданных значений ценностей , и .
Положим
и
.
Тогда, из первого дерева решений (случай,
когда Нэнси знает решение тренера),
оптимальное решение для Нэнси – заключить
пари, вне зависимости от решения тренера.
Допустим, в первом дереве, событие
верхней ветви (решение тренера попытаться
забить гол) наступает с вероятностью
,
а нижняя, соответственно, с вероятностью
,
тогда математическое ожидание (до того,
как будет известно решение тренера):
(1)
Из второго дерева решений, ожидаемый выигрыш от ставки положительный и равен правой части выражения (1), т.е. для Нэнси в любом случае лучше заключить пари, вероятность для нее не важна. Таким образом, для данного примера, когда и , не имеет значения, знает ли Нэнси решение тренера или нет.
Положим
и
;
команде не везет с тачдаунами, но она с
большой вероятностью может забить гол.
Из первого дерева решений, оптимальным
решением будет сделать ставку в том
случае, если тренер решил попытаться
забить гол, а не совершить тачдаун,
тогда:
(2)
Исходя из второго дерева решений, видно,
что оптимальным решением для Нэнси
будет заключать пари только в том случае,
если она считает, что вероятность
принятия тренером решения попытаться
забить гол выше, чем 0.68, тогда мат.
ожидание будет равно
,
что всегда меньше, чем (2). Например, если
она предполагает, что вероятность того,
что тренер решит попробовать забить
гол составляет 95%, то ее ожидаемый доход
составляет 0.158, тогда как (2) дает 0.178.
Разница 0.02 и есть ценность точной
информации о решении тренера перед
заключением пари. Если бы она предполагала,
что вероятность принятия тренером того
или иного решения – 50 на 50, то она бы не
заключала пари, а ценность точной
информации в таком случае, увеличилась
бы до 0.094.
Исходя из всего вышесказанного, имеем:
Задача об американском футболе (в)
Неформальная постановка задачи
Напомним, что два друга, Нэнси и Рон, наблюдая за футбольным матчем, решили заключить пари на исход матча после того, как тренер примет решение попытаться забить гол или совершить еще один тачдаун. Нэнси предлагает следующие ставки Рону, и он соглашается:
Если тренер решится на попытку тачдауна, и его команда победит, Рон должен Нэнси $2. Если же не выиграют, тогда Нэнси платит Рону $1.
Если тренер принимает решение попробовать забить гол, и команда выигрывает, Рон платит Нэнси $v, если проигрывают, то Нэнси платит $1.
В отличие от предыдущей задачи, мы предполагаем, что они еще не решили насколько большим будет значение v. Мы хотим сравнить две ставки для различных значений v, чтобы понять, влияет ли это значение на принимаемое решение или нет.
Формальная постановка задачи
В условиях предыдущей задачи, очевидно,
что v должно быть
меньше $2 (шанс заработать одно очко
гораздо выше, чем шанс получить два
очка, разумно на результат с более
высоким процентом выигрыша поставить
меньший коэффициент). Мы также знаем,
что каждая из условных вероятностей
(напомним, что
)
должна находиться в интервале между 0
и 1, таким образом, мы имеем:
.
Дерево решений данной задачи выглядит
так:
Расчет полезностей решений
Ценности исходов (альтернатив), с учетом новой введенной переменной теперь определяются так:
;
;
;
;
;
;
Полезности решений принимают вид:
При
:
,
При
:
,
.
Как видно, изменилось выражение только для случая, когда тренер решается на попытку забить гол.
Выбор решения
Нэнси считает, что
.
Более того, если она хочет, чтобы обе
ставки имели неотрицательное мат.
ожидание (получаемый ею доход), должны
быть выполнены следующие два неравенства:
и
,
- вероятности безразличия, т.е. критические
значения вероятностей
,
при которых уже нет разницы: заключать
пари или нет. Если мы построим график
значений
,
которые удовлетворяют вышеприведенным
неравенствам, то получим область I,
показанную на графике. Любые комбинации
в этой области дают положительный
ожидаемый доход.
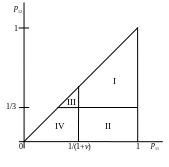
Таким образом, если попадают в область I, то оптимальное решение не зависит от решения тренера, доход всегда будет положительным. Если попадают в область II, то ожидаемый доход будет положительным только в том случае, если тренер решит попробовать забить гол, в III области – если решит совершить тачдаун. Т.к. мы полагаем, что Нэнси знает решение тренера, области I, II и III можно объединить в одну. Оставшаяся, четвертая область области допустимых значений, включает те значения , при которых ожидаемый доход всегда будет отрицательным, вне зависимости от того, что решит тренер. В итоге, имеем:
Область I: если или - заключать пари;
Область II: если - заключать пари, если - не заключать;
Область III: если - не заключать пари, если - заключать;
Область IV: если или - не заключать пари.
Обратите внимание, что, при v > 2, нет области III; любая комбинация (с учетом ), которая дает положительный доход, если тренер решает попытаться совершить тачдаун, так же дает положительный доход и при решении тренера попробовать забить гол.
Теперь рассмотрим более подробно области с положительным ожидаемым доходом. В области I решение тренера не влияет на решение Нэнси, при этом:
.
Это «уравнение безразличия» показано
на рисунке ниже в виде прямой линии
,
проходящей через левый нижний угол
области I. Точки
,
лежащие на одной из сплошных линий
областей I, II
и III и имеющие одинаковый
ожидаемый доход, дают значение вероятности
принятия тренером решения попытаться
забить гол
.
Эти линии называются изоконтурами.
Оптимальным ожидаемым доходом в области
IV является 0, в области
III – линия, параллельная
оси
,
в области II – линия,
параллельная оси
,
а в области I – линия,
возрастающая с ростом
и убывающая по
.
В случае, когда Нэнси, перед заключением пари, не знает о решении тренера, она должна оценить вероятность принятия тренером того или иного решения. Мы предполагаем, что ее решение будет заключаться в том, что бы заключать пари только в том случае, если ожидаемый доход будет неотрицательным. Напомним, что - вероятность принятия тренером решения попытаться забить гол. Тогда:
.
Нэнси заключит пари, только если первое
выражение будет больше нуля; ее решение,
разумеется, зависит не только от значения
,
но так же и от
и
.
Задачи принятия решений с ограниченным сроком хранения