3. Задача о защите территории
Неформальное описание задачи
Задача о защите территории аналогична задаче о защите посевов, но представлена в постановке, принятой в военном деле. Пусть некий военноначальник несет ответственность за безопасность вверенной ему территории. Существует угроза нападения на территорию противника, в этом случае территории будет нанесен значительный ущерб. Существует возможность провести оборонительные мероприятия, которые позволят защитить территорию в случае нападения противника, однако подобные мероприятия являются дорогостоящими. Военноначальнику требуется выбрать один из двух возможных вариантов решений – проводить мероприятия по защите территории или не проводить мероприятия по защите территории. При выборе первого варианта решения в случае нападения противника атака будет успешно отражена и территории будет причинен незначительный ущерб, в случае не нападения противника будут понесены лишние затраты на оборонительные мероприятия. При выборе второго варианта решения в случае нападения противника территории будет нанесен значительный ущерб, а в случае не нападения противника территория не понесет никаких потерь.
Формальная постановка задачи
Множество решений , где – решение проводить мероприятия по защите территории от нападения, – решение не проводить мероприятия по защите территории от нападения.
Поведение потенциального врага
описывается случайной величиной Y,
принимающей значения из множества
,
где
- противника нападет на территорию,
- противника не нападет на территорию.
Вероятность события
обозначим
символом
.
В зависимости от принятого военноначальником решения и поведения потенциального противника можно выделить четыре исхода (альтернативы), входящие в множество исходов (альтернатив) , где: - потенциальный противник осуществил нападение на территорию, однако территория защищена, в результате атака успешно отражена, понесены незначительные потери в ходе военных действий и расход на оборонительные мероприятия, - потенциальный противника не осуществлял нападения, однако территория была защищена, в результате понесен расход на оборонительные мероприятия, - потенциальный противник осуществил нападение на территорию, и территория не была защищена, в результате территории нанесен значительный ущерб, - потенциальный противника не осуществлял нападения, и не проводились мероприятия по защите территории, в результате территория не понесла никаких потерь.
Каждому из возможных исходов
(альтернатив)
поставим в соответствие функцию потерь
,
значение которой определяеся размером
затрат. Для потерь рассмотренных
альтернатив справедливо следуещее
соотношение:
<
.
На рисунке ниже представлено дерево решений для рассматриваемой задачи.
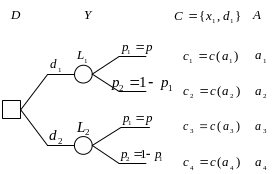
В данной задаче множество лотерей состоит из двух элементов . На рисунке ниже лотереи приведены в развернутом виде с указанием вероятностей исходов.
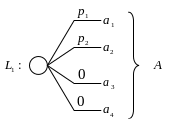
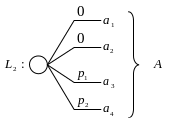
Диаграммы влияния
Диаграмма влияния для рассматриваемой задачи имеет вид
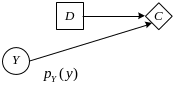
Определение риска от принятия решений
Для оценки качества принимаемого решения при байесовском подходе может быть использовано математическое ожидание потерь, которое в дальнейшем будем называть риском от принятия решения. Таким образом, риск от принятия решения определим как
,
где Е – символ математического
ожидания,
,
,
– ограниченная вещественнозначная
функция потерь, которая паре
,
или, что то же самое, соответствующей
альтернативе сопоставляет некоторый
расход
.
Расчет потерь от решений
Потери от исходов (альтернатив) определяются с учетом введенных обозначений как
;
;
.
Соотношение функции ценности и функции потерь. Для ЛПР альтернатива a предпочтительнее альтернативы b, если полезность альтернативы a больше полезности альтернативы b:
,
или если потери от альтернативы a меньше, чем потери от альтернативы b:
.
Для перехода от функции ценности к
функции потерь подходит любая убывающая
функция. В задаче о защите посевов для
перехода к функции потерь может быть
использована функция
.
Тогда для примера 3 значения потерь
равны:
- расходы для альтернативы
включают затраты на защиту посевов и
ущерб, нанесенный посевам заморозками;
- расходы для альтернативы
включают затраты на защиту посевов;
- расходы для альтернативы
определяются потерями от утраты урожая;
- в случае альтернативы
расходов нет.
Риск от решения или, что то же самое, лотереи равен:
.
Риск от решения или, что то же самое, лотереи равен:
Выбор решения
Байесовский подход к выбору решения.
Байесовский подход предполагает выбор
решения
,
минимизирующего математическое
ожидание потерь. При наличии всего двух
альтернатив лучшее в байесовском смысле
решение находится путем сравнения
соответствующих рисков:
,
где для определенности при равенстве рисков принимается решение .
Поскольку разности между значениями потерь остались теми же, что были разности между значениями ценностей, то можно предположить, что и остальные полученные результаты, в частности байесовское решение, осторожное решение и вероятность безразличия останутся прежними.
Байесовское решение имеет вид:
,
где вероятность безразличия определяется из соотношения:
,
после преобразования выражение имеет вид
,
откуда
.
В числовом примере 3 при использовании
функции потерь вместо функции ценности
вероятность безразличия не изменяется:
;
байесовское решение так же не изменяется:
.
Осторожный подход к выбору решения.
Осторожный (максиминный) подход
предполагает выбор решения
,
минимизирующий потери, при самом
неблагоприятном поведении окружающей
среды, в качестве которой в настоящей
задаче выступает поведение противника.
Аналогично задачи о защите посевов
.
Полезность точной информации
Пусть у военноначальника есть возможность получить точные данные о поведении противника. Полезность точной информации для сторонника байесовского решения с учетом результатов, полученных в задаче о защите посевов, равна:
.
График функции
показан на рисунке ниже.
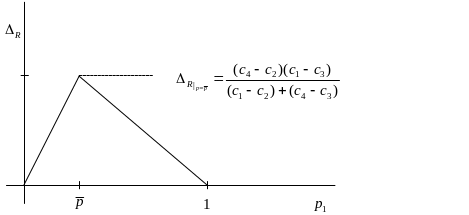
При вычислении значения
вероятность нападения противника
считается известной. Вычисленное
значение
определяет в единицах потерь цену точной
информации, выше которой не следует за
нее платить. Максимального значения
полезность точной информации достигает
при
,
что и определяет ситуацию наибольшей
неопределенности, когда стоимость
точной информации наиболее высока.
Для сторонника осторожных решений полезность точной информации может быть вычислена как
.
График функции показан на рисунке ниже.
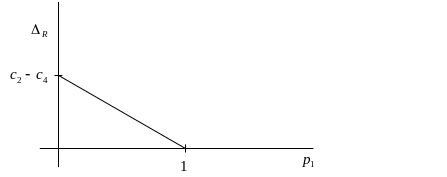
Максимального значения полезность
точной информации достигает при
,
поскольку при
,
даже сторонник осторожных решений не
будет защищать территорию.