2. Задача о защите посевов

Неформальное описание задачи

Пусть некий фермер выращивает растения не устойчивые к низким температурам. При температуре ниже нуля градусов посевы замерзнут, и урожай будет полностью потерян. Существуют методы защиты посевов от заморозков, которые позволяют частично сохранить урожай, однако они являются достаточно дорогостоящими. Фермеру требуется выбрать один из двух возможных вариантов решений – защищать посевы от заморозков или не защищать посевы от заморозков. При выборе первого варианта решения фермер частично сохранит урожай вне зависимости от погоды, однако затратит значительные средства на защиту посевов. При выборе второго варианта, в случае теплой погоды, фермер получит высокий доход, а в случае заморозков полностью потеряет урожай и понесет большие убытки. Для оценки качества принимаемого решения будем использовать математическое ожидание получаемого фермером дохода.

Формальная постановка задачи

Множество решений , где – решение защищать посевы от заморозков, – решение не защищать посевы от заморозков.

Погода описывается случайной величиной Y, принимающей значения из множества , где - наблюдаются заморозки, - наблюдается устойчивая теплая погода. Вероятность события обозначим символом . При необходимости будем использовать также символ .

В зависимости от принятого фермером решения и наблюдаемой погоды можно выделить четыре исхода (альтернативы), входящие в множество исходов (альтернатив) , где: - наблюдаются заморозки, однако посевы защищены, в результате посевы сохранены частично, фермер получает низкий доход, - заморозки не наблюдаются, при этом посевы защищены, в результате посевы сохранены полностью, фермер получает средний доход, - наблюдаются заморозки, но посевы не защищены, в результате посевы погибают полностью, фермер несет большие убытки, - заморозки не наблюдаются и посевы не защищены, в результате посевы сохранены полностью, фермер получает высокий доход.

Каждому из возможных исходов поставим в соответствие ценность исхода (альтернативы) , значение которой определяеся получаемым доходом. Для ценностей рассмотренных альтернатив справедливо следующее соотношение: > .

На рисунке ниже представлено дерево решений для рассматриваемой задачи.

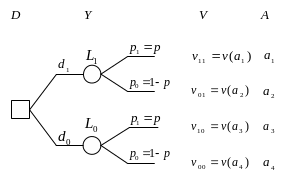
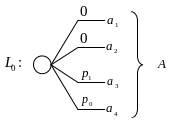
В данной задаче множество лотерей состоит из двух элементов . На рисунке ниже лотереи приведены в развернутом виде с указанием вероятностей исходов.

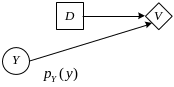
Диаграммы влияния

Диаграмма влияния для рассматриваемой задачи имеет вид

Расчет полезностей решений

Ценности исходов (альтернатив) определяются с учетом введенных обозначений как

;

;

.

Полезность решения (лотереи ) равна

.

Полезность решения (лотереи ) равна

.

Выбор решения

Байесовский подход к выбору решения. В условиях наличия двух альтернатив лучшее в байесовском смысле решение находится путем сравнения соответствующих полезностей:

.

С учетом полученных значений полезности решений получаем:

,

Тогда байесовское решение имеет вид:

(2).

Вероятность безразличия – значение вероятности , при котором принятое решение не оказывает влияния на математическое ожидание получаемого дохода:

,

тогда справедливо:

,

откуда вероятность безразличия равна:

(3).

Выражение (2) с учетом (3) имеет вид:

Полезность байесовского решения:

Осторожный подход к выбору решения. При самом неблагоприятном поведении окружающей среды, т.е. в случае заморозков, доход, получаемый фермером при принятии решений и соответственно равен:

.

Поскольку доход по условию задачи больше дохода , осторожное (максиминное) решение есть . Полезность осторожного решения .

Пример 3

Пусть стоимость урожая равна 100 единиц, стоимость защиты урожая от заморозков составляет 25 единиц. Известно, что потеря урожая от заморозков для незащищенных посевов составляет 100%, а для защищенных посевов – 25%. В случае, если фермер теряет весь урожай, он вынужден платить неустойку в размере 50 единиц. Вероятность заморозков , вероятность теплой погоды . Требуется найти байесовское и осторожное решения, рассчитать вероятность безразличия.

По условию задачи ценности альтернатив равны:

;

;

;

.

Для определения байесовского решения в соответствии с (2) вычисляем:

,

следовательно .

Очевидно, что осторожное решение также равно : .

Вероятность безразличия в соответствии с (3) равна:

.

Полезность точной информации

Пусть у фермера есть возможность получить точный прогноз погоды, обратившись в компетентный метеоцентр. Наличие точной информации исключает неопределенность при принятии решения. Дерево решений в такой информационной ситуации имеет вид:

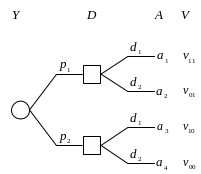
Наилучшее решение при отсутствии неопределенности принимается фермером исходя из известного значения x случайной величины Y:

Полезность решения :

Диаграммы влияния

При наличии точной информации диаграмма влияния имеет вид:

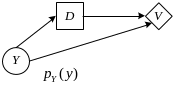
Рассмотрим теперь вопрос о целесообразности покупки точной информации о погоде и о сумме, дороже которой за такую информацию не имеет смысла платить. Вычислим полезность точной информации для фермера, склонного к принятию байесовских решений:

Если , то .

В примере 3 .

График функции (p₁) показан на рисунке ниже.

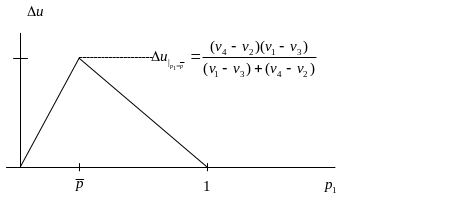
При вычислении значения вероятность заморозков считается известной. Вычисленное значение определяет в единицах дохода цену точной информации, выше которой фермеру не следует за нее платить. Максимального значения полезность точной информации достигает при , что и определяет ситуацию наибольшей неопределенности, когда стоимость точной информации наиболее высока.

Для сторонника осторожных решений полезность точной информации может быть вычислена как

.

График функции показан на рисунке ниже

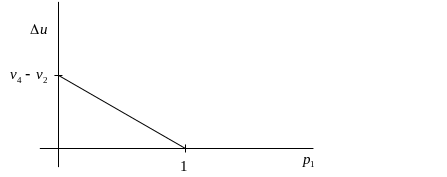
Максимального значения полезность точной информации достигает при , поскольку при , даже сторонник осторожных решений не будет защищать посевы. В остальных ситуациях, когда есть вероятность мороза, будет отдано предпочтение решению защищать посевы.