Министерство образования и науки РФ

_____________________________________________________

Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»

______________________________________________________

Д. В. Куликов, Н. А. Жукова

Задачи принятия решений

Учебное пособие

Санкт-Петербург

Издательство СПбГЭТУ «ЛЭТИ»

2013

УДК 681.3.06 (075.08)

ББК 00000000

Б 20

Б 20 Куликов Д. В., Жукова Н. А. Задачи принятия решений: Учеб. пособие. СПб.: Изд-во: СПбГЭТУ «ЛЭТИ», 2013. 64 с.

ISBN 0-0000-0000-0

Методическое пособие по курсу лекций «Теория принятия решений» в предлагаемом вашему вниманию виде с 2006 года читается на кафедре МО ЭВМ для студентов третьего курса специальности «Программное обеспечение ЭВМ». Основной целью курса является ознакомление студентов с задачами, моделями и методами принятия решений в различных информационных ситуациях, а также с обоснованием оптимизационных моделей, широко используемых в практике принятия решений.

Курс состоит из двух разделов, первый из которых содержит набор простых задач принятия решений в условиях неопределенности. В процессе постановки и решения задач студенты знакомятся с основными понятиями и схемами принятия решений. Второй раздел курса с единых позиций рассматривает и сопоставляет различные модели, используемые в принятии управленческих решений. В настоящем пособии предложены материалы по первому разделу курса.

УДК 681.3.06 (075.08)

ББК 00000000

Рецензенты:

Утверждено

редакционно-издательским советом университета

в качестве учебного пособия

ISBN 0-0000-0000-0 © СПбГЭТУ «ЛЭТИ», 2013

Введение

Под лицом, принимающим решение, (ЛПР) понимается человек или группа людей, принимающих решение и несущих за него ответственность.

Рассмотрим пример простейшей задачи принятия решений. ЛПР необходимо из множества возможных решений выбрать одно решение , , . Каждому возможному решению сопоставляется некоторый исход (альтернатива) , где - множество возможных альтернатив, , . Задача ЛПР заключается в выборе наилучшей альтернативы. На рисунке показано дерево решений.

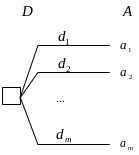
Если альтернативы представлены с помощью некоторой количественной шкалы, то выбор сводится к выбору наибольшего (наименьшего) из чисел. Ценность каждой альтернативы может определяться, например, как значение некоторой функции , называемой функцией полезности, . Как правило, , , причем , , где - наихудший и наилучший варианты.

Если построена функция ценности , то принятие решения сводится к решению задачи оптимизации , при этом интерпретируется как целевая функция. Один из вопросов, рассматриваемых в курсе – всегда ли существует функция ценности, и, если нет, то каким свойствами должны обладать предпочтения ЛПР на множестве альтернатив для того, чтобы функция существовала и обладала следующим свойством:

, (*)

где - бинарное отношение на множестве альтернатив , характеризующее предпочтения ЛПР.

Многокритериальные задачи

Часто альтернатива естественным образом может быть представлена как вектор , где - значение фактора (атрибута) и .

В этом случае задача выяснения существования и построения функции ценности вида (*) формируется как задача агрегирования частных функций ценности .

Ценность альтернативы описывается вектором ( ), где , . Естественным представляется желание построить агрегированную функцию ценности : . В простейшем случае такая функция имеет вид: .

Понятно, что построение в таком виде возможно далеко не всегда. Если агрегированная функция не существует, то возникает задача непосредственного сравнения векторов , и выбора из них лучшего. Эта задача является основной при решении многокритериальных задач.

Задачи с неопределенностью

Почти всегда в задаче принятия решений присутствует неопределенность, не позволяющая отождествить некоторое решение , и альтернативу . Дерево решений для рассматриваемой ситуации показано на рисунке.

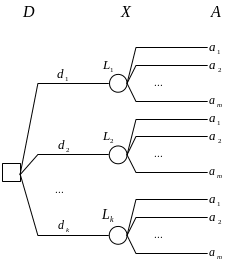
Неопределенность описывается с помощью случайной величины X на множестве альтернатив , распределение случайной величины зависит от принятого решения и описывается в непрерывном случае семейством плотностей распределения , , . В дискретном случае .

Поскольку распределение случайной X зависит от принятого решения, в ТПР часто говорят, что каждое решение связано с лотереей . Поскольку нет возможности непосредственно выбрать желаемую альтернативу даже, если она известна, то приходится выбирать между лотереями , что заметно сложнее выбора из множества альтернатив. Хотелось бы иметь функцию полезности (ожидаемой)

, (**)

где - множество лотерей, т.ч. , и кроме того хотелось бы, чтобы она легко вычислялась.

Если на множестве альтернатив задана функция ценности , , то для сравнения лотерей можно вычислить математическое ожидание функции ценности каждой из лотерей и принять , . Для непрерывного случая , для дискретного случая .

Выясняется, что при выполнении ряда предположений касательно предпочтений ЛПР на множестве лотерей функция действительно существует.

Если же функция не агрегирована, но представлена как множество векторов , то все равно хотелось бы научиться строить функцию полезности (**) в виде , , где - аддитивная или мультипликативная функция. Опять же выясняется, что при выполнении ряда предположений о предпочтениях ЛПР на множестве лотерей существует возможность построения функции полезности в аддитивном или мультипликативном виде.

Особый круг проблем возникает в случае, когда решение принимается коллективом и требуется согласование интересов. В курсе рассмотрены некоторые подходы к принятию коллективных решений, в число которых входит теория игр, предметом которой является принятие решений в конфликтных ситуациях.

Задачи принятия решений

1а. Задача об инвестировании средств (вариант а)

Неформальное описание задачи.

Пусть некий начинающий инвестор, имеющий в своем распоряжении небольшую сумму денег и большое желание преумножить имеющийся капитал, рассматривает два варианта вложения средств – в акции и в облигации с купонным доходом. Вариант вложения в облигации является надежным, однако имеет достаточно низкую доходность. При вложении средств в акции в связи с непредсказуемостью поведения рынка существует вероятность потерять вложенные средства. Задача сводится к выбору наилучшего варианта из двух рассматриваемых. Для оценки качества принимаемого решения будем использовать математическое ожидание получаемого инвестором дохода.

Формальная постановка задачи.

Введем в рассмотрение множество решений , где – решение инвестировать в облигации, – решение инвестировать в акции.

Поведение рынка акций будем описывать случайной величиной Y, принимающей значения из множества , где – рынок растет, – рынок падает. Вероятность события обозначим символом При необходимости будем использовать также символ ( y_i). Отметим, что в силу незначительности инвестируемых средств, принимаемое инвестором решение не влияет на поведение рынка акций и не изменяет вероятностей развития событий.

В зависимости от принятого инвестором решения и поведения рынка можно выделить три исхода (альтернативы), входящие в множество исходов (альтернатив) , где: – успешное вложение в акции, – успешное вложение в облигации, – неуспешное вложение в акции.

Каждому из возможных исходов поставим в соответствие значение получаемого инвестором дохода , которое назовем ценностью исхода (альтернативы)

Для наглядности представим задачу в виде дерева решений так, как это сделано на рисунке ниже.

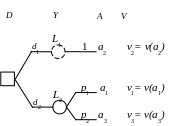
Элемент принятия решения здесь имеет квадратную форму, а кружки соответствуют ситуациям неопределенности, в которые попадает инвестор после того, как средства вложены. Далее такие ситуации мы будем называть лотереями В данной задаче будем рассматривать множество, состоящее из двух лотерей . Каждая из лотерей полностью описывается распределением вероятностей на множестве альтернатив, причем лотерея – вырожденная, поскольку с вероятностью, равной единице, приводит к исходу .

На рисунке ниже лотереи приведены в развернутом виде с указанием вероятностей исходов.

L₁: L₂:

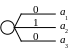
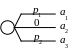
Определение полезностей решений

Для оценки качества принимаемого решения используем математическое ожидание получаемого инвестором дохода, которое в дальнейшем будем называть полезностью или ожидаемой полезностью решения. Такой подход к оценке качества решения часто называют байесовым или байесовским. Полезность решения определим как

,

где Е – символ математического ожидания, , , – ограниченная вещественнозначная функция ценности (дохода), которая паре , или, что то же самое, соответствующей альтернативе сопоставляет некоторый доход .

Расчет полезностей решений

Ценности исходов (альтернатив) определяются с учетом введенных обозначений как

;

;

.

Полезность решения полностью определяется ценностью альтернативы в силу вырожденности лотереи :

.

Полезность решения d₂ или, что то же самое, лотереи L₂ равна

.

Выбор решения

Байесовский подход предполагает выбор решения , максимизирующего математическое ожидание дохода. При наличии всего двух альтернатив лучшее в байесовском смысле решение легко находится путем сравнения соответствующих полезностей:

,

где для определенности при равенстве полезностей принимается решение :

.

Пусть - вероятность безразличия (indifference probability) – значение вероятности , при котором принятое решение не оказывает влияния на математическое ожидание получаемого дохода. Тогда

,

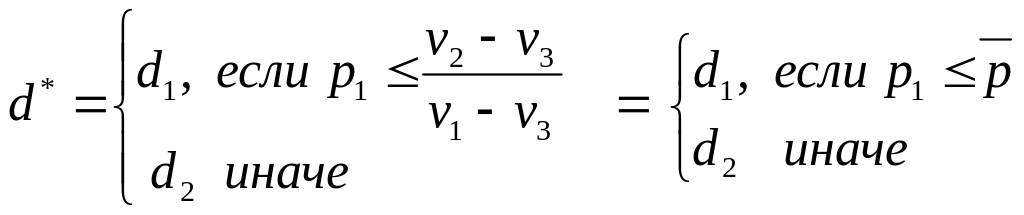где

.

При вычислении вероятности безразличия использовано следующее соотношение доходностей исходов:

;

Альтернативой байесовскому походу к определению лучшего решения является подход осторожный. Осторожный (максиминный) подход предполагает выбор решения , максимизирующего доход, получаемый инвестором при самом неблагоприятном поведении окружающей среды, в качестве которой в настоящей задаче выступает рынок акций. Нетрудно видеть, что здесь

.

И, поскольку доход от инвестирования средств в рынок облигаций по условию задачи больше дохода от инвестирования в рынок акций при неблагоприятном для рынка акций развитии событий, осторожное (максиминное) решение есть , а полезность этого решения .

Полезность точной информации

Представим себе, что перед принятием решения о вложении средств инвестор получает достоверную информацию о будущем поведении рынка (о реализации случайной величины Y), что исключает неопределенность при принятии решения. Дерево решений в такой информационной ситуации имеет вид

:

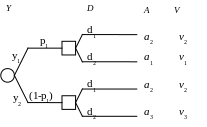
Наилучшее решение при отсутствии неопределенности принимается инвестором исходя из известного значения y случайной величины Y:

.

Полезность решения :

.

Рассмотрим теперь вопрос о целесообразности покупки точной информации и о сумме, дороже которой за такую информацию не имеет смысла платить. Вычислим полезность точной информации для инвестора, склонного к принятию байесовских решений, как:

.

Тогда

График функции (p₁) показан на рисунке ниже.

При вычислении значения вероятность благоприятного развития событий на рынке акций считается известной. Вычисленное значение определяет в единицах дохода цену точной информации, выше которой инвестору не следует за нее платить. Максимального значения полезность точной информации достигает при , что и определяет ситуацию наибольшей неопределенности, когда стоимость точной информации наиболее высока.

Для сторонника осторожных решений полезность точной информации может быть вычислена как

,

хотя само вычисление полезности может и не иметь смысла для осторожного инвестора, не признающего байесовского подхода к принятию решений.

Диаграммы влияния

Альтернативным построению дерева решений способом наглядного представления задачи принятия решения является диаграмма влияния, которая для исходной задачи имеет вид:

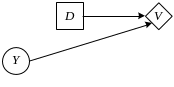
При наличии точной информации диаграмма влияния преобразуется к виду

Смысл диаграмм влияния интуитивно ясен из приведенных рисунков.

Пример 1

Пусть общая сумма инвестируемых средств составляет 10000 единиц. Зададим значения дохода, получаемого инвестором как:

v₁ = 5000;

v₂ = 1000;

v₃ = –5000.

Тогда = 0,6;

∆ _u( ) = * (v₁ - v₂) = 2400.