Откуда перевозят

1 2 3

Перевозка из третьего источника сырья на схеме не показана.

Обозначим количество груза, перевезенного

из пункта 1 в пункт 1 через Х₁₁,

из пункта 1 в пункт 2 через Х₁₂,

из пункта 1 в пункт 3 через Х₁₃,

из пункта 2 в пункт 1 через Х₂₁ и т.д.

Необходимо минимизировать общую стоимость перевозок F. Воспользовавшись матрицей стоимости С, составим уравнение этой стоимости. В общем виде

F= а ₁₁Х ₁₁ +а ₁₂ Х ₁₂ + а ₁₃Х ₁₃ + а ₁₄Х ₁₄ + а ₂₁Х ₂₁+а ₂₂Х ₂₂ +а ₂₃Х ₂₃ + +а ₂₄Х ₂₄ + а ₃₁ Х ₃₁+а ₃₂Х ₃₂

+а₃₃Х ₃₃ + а ₃₄Х₃₄

или в цифрах: F=7X ₁₁+8X ₁₂+1X ₁₃+2X ₁₄ +4X ₂₁+5X ₂₂+9X ₂₃+8X ₂₄+9X₃₁+2X ₃₂+ +3X ₃₃+X₃₄

Запасы сырья в каждом пункте отправления и потребности в нем в каждом пункте переработки ограничены.

Для первого пункта переработки

Х₁₁+Х ₂₁+ Х ₃₁=120.

Соответственно, для остальных пунктов переработки имеем:

Х₁₂+Х ₂₂+Х ₃₂ = 50,

Х ₁₃+ Х ₂₃+ Х ₃₃=190,

Х ₁₄+Х ₂₄+Х ₃₄ =110.

Для пунктов отправки сырья имеем:

Х ₁₁+Х ₁₂+Х ₁₃+Х ₁₄ =160

Х ₂₁+Х ₂₂+Х ₂₃+Х ₂₄= 140

Х ₃₁+Х ₃₂+Х ₃₃+Х ₃₄ =170

Кроме того, так как мы возим сырье только в одну сторону, все переменные должны быть положительными:

X ₁₁>0 ,X ₁₂> 0, X ₁₃>0, X ₁₄>0, X ₂₁>0, X ₂₂>0,X ₂₃>0, X ₂₄>0,X₃₁>0, X ₃₂>0,X ₃₃>0,X ₃₄>0.

Решаем задачу в Маткаде.

Наберем начальные значения переменных X (по-прежнему равные 1), целевую функцию, все ограничения и все числа аналогично задачам 1 и 2. Получим решение.

Математическую запись решения можно записать более компактно, используя матричное исчисление.

Все переменные задаем в форме матрицы. Заметив, что целевая функция может быть представлена в виде следа ( суммы диагональных элементов) произведения АХ^Т, где Т – индекс транспонирования, записываем ее в такой форме. Все ограничения записываем также сокращенно. Ответ получен в виде матрицы z.

И так, следует перевезти из пункта 1 в пункт приема 3 160 единиц груза, из пункта 2 в пункт приема 1 – 120 единиц и в пункт 2 – 20 единиц.

Из пункта отправки 3 следует перевезти в пункты приема 2 и 3 по 30 единиц, а в пункт приема 4 – 110 единиц груза. При этом минимальные затраты составят 1000 единиц стоимости.

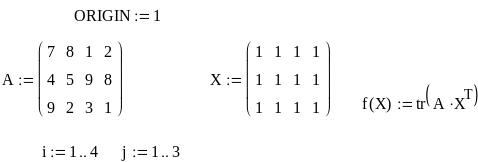
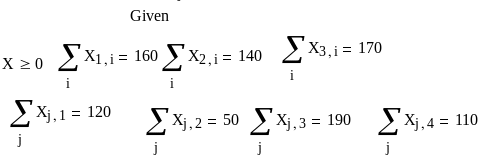
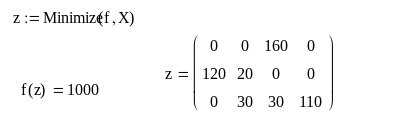
Задача 4.

Имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i – ого пункта производства в j – центр распределения C_ij приведена в таблице, где под строкой понимается пункт производства, а под столбцом пункт распределения. Кроме того, в этой таблице в i-строке указан объем производства в i-м пункте производства, а в j – м столбце указан спрос в j – м центре распределения. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.

Стоимость перевозки единицы продукции				Объем производства
1	3	4	5	20
5	2	10	3	30
3	2	1	4	50
6	4	2	6	20
42	40	80	38

Решение задачи средствами MathCAD:

1. Введем исходные данные в матричной форме:

2. Вводим линейную целевую функцию

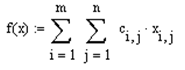
3. Зададим начальные условия переменных:

4. Вводим ограничения задачи в матричной форме.

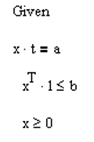
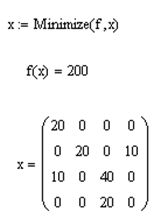
5. Определяем оптимальное решение задачи с помощью встроенной функции Minimize:

Задача 5.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10-ю часами в сутки. Время обработки и прибыль от продажи одного изделия каждого вида приведены в таблице. Найти оптимальный объем производства изделий каждого вида.

Время обработки и прибыль от продажи одного изделия

Изделие	Время обработки изделия, мин			Удельная прибыль
	Станок 1	Станок 2	Станок 3
1	10	6	8	2
2	5	21	17	3

Решение задачи средствами MathCAD:

1. Введите исходные данные в матричной форме.

2. Определите линейную целевую функцию.

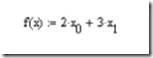
3. Задайте начальные значения переменных:

4. Вводите ограничения задачи в матричной форме.

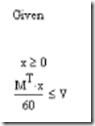
5. Maximize: