Нормальная форма игры.
В
игре может участвовать несколько
игроков. Можно давать игрокам имена,
однако, в общетеоретическом плане это
неудобно. Игроков принято нумеровать,
и в качестве обозначения игрока
использовать его номер. Таким образом,
одним из элементов игры является
множество игроков
,
где n
– номер последнего игрока (или количество
игроков). Каждый
игрок
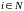имеет множество стратегий
(действий, альтернатив)
.
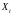Задачей игрока является выбор конкретной
стратегии
.
Если каждый из игроков осуществил свой
выбор, то говорят, что реализовался
исход
игры. Исходом называется n-мерный
вектор
.
Исходы имеют для игроков разную ценность.
Рациональный игрок должен стремиться
к достижению как можно более благоприятного
для себя исхода. Однако никакой игрок
не в состоянии обеспечить наилучший
для себя исход только за счет собственных
действий. Принимая решение о выборе
действия, он должен учитывать интересы
и возможные действия других игроков,
влияющие на исход игры. В этом состоит
отличие теоретико-игровой постановки
задачи принятия решений от задачи
оптимизации.
В
общем случае неравноценность исходов
описывается при помощи систем
предпочтений игроков.
Если, например, игрок i
считает, что из трех исходов
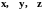наилучшим для него является x,
а наихудшим z,
то пишут, что
.
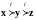В частном случае предполагают, что
каждый игрок имеет свою функцию
полезности
,
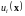областью определения которой является
множество исходов, а множеством значений
– множество действительных чисел.
Функция определяется таким образом,
что более предпочтительному исходу
соответствует большее число. Так, для
вышеприведенного примера:
.
Резюмируя
можно сказать, что игра
в
нормальной (или
стратегической) форме
это
тройка:
.
Задачей каждого игрока i
является выбор такой стратегии
,
при которой его функция полезности
принимает возможно большее значение.
Примеры. Особенно просто задавать игры двух лиц. Для этого некоторого игрока условно называют первым, а другого - вторым. И рисуют таблицу, где строки соответствуют стратегиям первого игрока, а столбцы - стратегиям второго. В клетках записывают выигрыши - сначала первого, затем второго. По этой причине такие игры называют биматричными. Проведем три простейших примера, которые будут часто встречаться.
Пример 1. Игра в чет/нечет. Игроки договариваются о следующих правилах игры. Каждый из них тайно загадывает натуральное число. Затем числа предъявляются и складываются. Если сумма оказывается четной, то второй игрок платит первому единицу денег, а если нечетной, то – наоборот. Понятно, что для каждого из игроков несущественно, какое именно число загадывать, существенно лишь то, является оно четным или нечетным. Поэтому для каждого из игроков можно ограничиться списком лишь из двух действий: четное или нечетное число. Матрица этой игры выглядит следующим образом:
|
|
Второй |
игрок |
|
|
чет |
нечет |
Первый |
чет |
1, -1 |
-1, 1 |
игрок |
нечет |
-1, 1 |
1, -1 |
Это пример игры с т.н. нулевой суммой.
2. Дилемма заключенного
|
yl |
y2 |
x1 |
5, 5 |
-1, 9 |
x2 |
9, -1 |
0, 0 |
Первые стратегии можно назвать "кооперативными", вторые – «эгоистическими». К такой игре приводит простейший вариант дуополии, когда первые стратегии - высокие цены, а второй - низкие.
3. Семейный спор
|
yl |
y2 |
x1 |
2, 1 |
0, 0 |
x2 |
0, 0 |
1, 2 |
Неформально: первый игрок - муж, второй - жена. Первые стратегии - идти на бокс, вторые - в театр. Мужу больше хочется пойти на бокс, жене - в театр, но им лучше вместе.
В совсем утрированном виде эта игра превращается в игру координации ("встреча в Нью-Йорке") с таблицей
1, 1 |
0, 0 |
0, 0 |
1, 1 |