4 Регрессионные модели исследования
ЗАВИСИМОСТЕЙ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
4.1 Разработка двухфакторной модели
Задание
Установить
параметры двухфакторной модели
определения эксплуатационных расходов
по передвижению груженых вагонов по
двухпутным электрифицированным участкам
сети в зависимости от влияния двух
факторов – профиля пути на этих участках
и расходной ставки на 1 кВт
ч;
оценить адекватность полученной модели
и рассчитать величину коэффициента
множественной регрессии.
Исходные данные для моделирования влияния двух факторов на величину эксплуатационных расходов по пропуску груженых вагонов приведены в таблице 4.1. Вариант исходных данных выбирается по первой букве фамилии студента.
Методические указания по выполнению задания
Существует несколько различных методов многофакторного моделирования экономических процессов, в том числе корреляционного и регрессионного анализа, метод статистических испытаний. Наиболее прост с точки зрения использования в практике моделирования метод регрессионного анализа.
Таблица 4.1 – Исходные данные
Номер наблюдения |
y |
Варианты |
|||||||
Г, Ж, О, Л |
З, Н, У, Ц |
Ф, Ю, В, Е |
И, Р, Т, Ч |
||||||
х1 |
х2 |
х1 |
х2 |
х1 |
х2 |
х1 |
х2 |
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
1,12 1,04 1,11 0,98 1,05 1,65 1,08 1,16 1,29 1,11 1,11 1,11 1,46 1,05 1,03 1,07 1,08 |
0,7 1,2 1,0 0,6 1,0 0,6 0,1 0,7 1,1 0,4 1,9 –0,7 1,6 –0,4 0,7 0,8 1,2 |
0,63 0,64 0,67 0,69 0,94 0,97 0,91 0,92 1,05 0.92 0,91 0,94 1,07 0,65 0,68 0,91 0,95 |
0,9 –0,2 1,3 0,0 0,6 1,5 0,1 0,7 1,2 0,3 0,4 0,2 1,6 0,3 –0,6 0,4 0,8 |
0,69 0,65 0,63 0,69 0,93 0,96 0,93 0,99 1,14 0.94 0,95 0,96 1,05 0,68 0,69 0,93 0,92 |
1,2 0,6 0,6 0,0 0,6 1,8 0,7 0,9 1,5 0,5 0,6 0,4 1,8 0,7 0,8 0,9 1,0 |
0,70 0,63 0,69 0,68 0,95 0,98 0,95 0,93 1,15 0.95 0,96 0,98 1,12 0,69 0,73 0,99 0,97 |
0,6 0,1 0,6 0,0 0,9 1,8 0,5 0,9 1,4 0,6 0,5 0,7 1,7 0,5 0,4 0,8 1,0 |
0,66 0,69 0,62 0,69 0,99 0,99 0,97 0,99 1,12 0.94 0,96 0,95 1,09 0,60 0,62 0,95 0,91 |
Окончание таблицы 4.1
Номер наблюдения |
Варианты |
|||||||
Х, Я, Б |
Д, М, П |
С, Ш, Э |
А, К, Щ |
|||||
х1 |
х2 |
х1 |
х2 |
х1 |
х2 |
х1 |
х2 |
|
1 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
0,7 1,2 1,0 0,6 0,1 1,9 0,1 0,7 1,1 0,4 1,9 –0,7 1,6 0,4 0,7 0,8 1,2 |
0,64 0,71 0,65 0,73 0,98 1,09 1,07 1,09 1,15 0.95 0,95 0,95 1,10 0,61 0,63 1,02 0,95 |
0,9 0,1 0,6 0,0 0,9 1,8 0,9 1,0 1,4 0,6 0,5 0,7 1,7 0,6 0,6 1,1 1,2 |
0,64 0,79 0,72 0,75 0,92 1,09 1,07 1,16 1,12 0.95 0,97 0,96 1,08 0,61 0,64 0,97 0,99 |
1,2 0,9 1,0 0,0 0,6 1,9 0,8 1,0 1,2 0,6 0,7 0,5 1,7 0,6 0,6 1,1 1,2 |
0,68 0,68 0,63 0,70 0,93 0,99 0,95 0,99 1,14 0.96 0,98 0,97 1,12 0,62 0,63 0,97 0,98 |
0,8 0,9 1,0 0,0 0,9 1,4 1,0 1,1 1,4 1,0 0,8 0,6 1,6 0,5 0,6 0,8 0,9 |
0,62 0,65 0,62 0,64 0,90 0,97 0,95 0,96 1,02 0.90 0,94 0,94 1,09 0,65 0,67 0,92 0,96 |
Математический аппарат моделирования состоит в следующем. Имеется n результатов наблюдений над величинами y, зависящий от m переменных х1, х2, … хm. Задача состоит в том, чтобы по результатам наблюдений определить параметры модели и оценить ее адекватность.
Многофакторные модели, выражающие тенденцию вариации изучаемого экономического явления в связи с изменениями факторов-переменных, можно изобразить в виде различных моделей. На практике наибольшее распространение получили линейные и приведенные к линейным модели. Основным достоинством линейных моделей является их простота, а методика их решения доступнее и лучше разработана. Линейная модель имеет вид
y
=c0
+
где с0 – параметр, не зависящий от исследуемых факторов;
сi – параметры , определяющие количественное влияние каждого фактора на величину функции, i = 1, 2, …, m;
xi – факторы-аргументы.
Параметры модели находят в ходе решения системы нормальных уравнений, например, методом наименьших квадратов. Для случая, когда на функцию у, характеризующую изучаемое явление, влияет изменение одновременно двух факторов x1 и х2, система уравнений имеет вид
Определив с0 и сi, найдем искомую модель
yx = c0 + c1x1 + c2x2.
Для оценки адекватности модели можно использовать и показатели средней ошибки аппроксимации, %,
ɛ =
Одновременное влияние независимых переменных xi на зависимую переменную у измеряется коэффициентом множественной регрессии R. Чем меньше наблюдаемые величине отклоняются от поверхности множественной регрессии, тем больше значение R. Для линейной модели
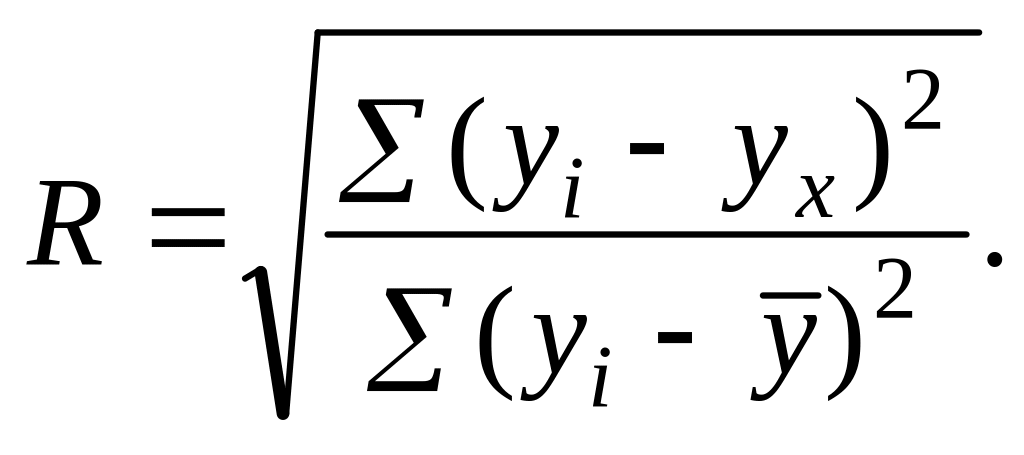
При небольшом числе наблюдений величина выборочного коэффициента множественной корреляции обычно завышается. Поэтому величину R корректируют:
Пример. 2. Рассмотрим процесс моделирования на примере определения эксплуатационных расходов по передвижению грузовых вагонов по двухпутным электрифицированным участкам сети у (тыс. руб./ваг.км), если известны величины эквивалентных уклонов x1, характеризующих профиль пути соответствующих участков, и расходная ставка на 1 кВт∙ч электроэнергии x2 (тыс. руб.). Для нахождения многофакторной модели используем исходные данные, приведенные в таблице 4.2. Там же дан порядок расчета промежуточных величин. Используя итоговые данные гр. 2–9 таблицы 4.2, запишем искомую систему уравнений:
Решив эти уравнения, получим c0 = 0,17, c1 = 0,02, и c2 = 1,14. Следовательно, искомая двухфакторная модель записывается так:
yx = 0,17 + 0,03x1 + 1,14x2.
Определяем все теоретические значения yx, которые для нашего примера приведены в гр. 11. Затем рассчитываем средние значения фактического и теоретического ряда величин эксплуатационных расходов:
Оцениваем точность модели – степень приближения теоретической поверхности регрессии к фактическим значениям:
ɛ =
.
На оценку адекватности влияют выбор формы модели, число наблюдений и точность расчетов. Расчетная средняя ошибка получилась равной 13 %, что свидетельствует о недостаточно высокой точности модели.
Таблица 4.2 – Иcходные данные и схема определения многофакторной модели
Номер наблюдения |
y |
x1 |
x2 |
|
x1x2 |
|
yx1 |
yx2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
1,16 1,08 1,12 0,98 1,06 1,75 1,06 1,15 1,27 1,10 1,10 1,10 1,44 1,00 1,00 1,06 1,09 |
0,7 1,2 1,0 0,6 0,1 0,6 0,1 0,7 1,1 0,4 1,9 –0,7 1,6 –0,4 0,7 0,8 1,2 |
0,64 0,64 0,68 0,69 0,93 0,98 0,90 0,97 1,04 0.91 0,90 0,93 1,06 0,64 0,67 0,90 0,98 |
0,49 1,44 1,00 0,36 0,01 0,36 0,01 0,49 1,21 0,16 3,61 0,49 2,56 0,16 0,49 0,64 1,44 |
0,448 0,768 0,680 0,414 0,093 0,588 0,090 0,679 1,144 0,364 1,710 –0,651 1,696 –0,256 0,469 0,720 1,176 |
1,410 0,410 0,462 0,476 0,865 0,960 0,810 0,941 1,082 0,828 0,810 0,865 1,124 0,410 0,449 0,810 0,960 |
0,812 1,296 1,120 0,588 0,106 1,050 0,106 0,805 1,397 0,440 2,090 –0,770 2,304 –0,400 0,700 0,848 1,272 |
0,742 0,691 0,762 0,676 0,986 1,715 0,954 1,116 1,321 1,001 0,990 1,023 1,526 0,640 0,670 0,954 1,068 |
Σ |
19,52 |
11,6 |
14,46 |
14,92 |
10,132 |
12,672 |
13,764 |
16,835 |
Окончание таблицы 4.2
Номер наблюдения |
|
|
|
|
|
|
|
1 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
0,01 0,07 –0,03 0,17 –0,09 0,60 0,09 0,00 0,12 –0,05 –0,05 –0,05 0,29 –0,15 –0,15 –0,09 –0,06 |
0,92 0,95 0,98 0,97 1,23 1,31 1,20 1,30 1,39 1,22 1,25 1,21 1,43 0,89 0,95 1,22 1,32 |
0,0001 0,0049 0,0009 0,0289 0,0081 0,3600 0,0081 0,0000 0,0144 0,0025 0,0025 0,0025 0,0841 0,0225 0,0225 0,0081 0,0036 |
0,00 –0,08 –0,04 –0,18 –0,10 0,59 –0,10 –0,01 0,09 –0,06 –0,06 –0,06 0,28 –0,16 –0,16 –0,10 –0,07 |
0,0000 0,0064 0,0016 0,0324 0,0100 0,3481 0,0100 0,0001 0,0081 0,0036 0,0036 0,0036 0,0784 0,0256 0,0256 0,0100 0,0049 |
0,24 0,13 0,14 0,01 –0,17 0,44 –0,14 –0,15 –0,12 –0,12 –0,15 –0,11 0,01 0,11 0,05 –0,16 –0,23 |
0,20 0,12 0,12 0,01 0,16 0,25 0,13 0,12 0,09 0,11 0,14 0,10 0,01 0,11 0,05 0,15 0,21 |
Σ |
0,45 |
19,74 |
0,5737 |
– |
0,5720 |
–0,22 |
2,22 |
Находим теперь величину коэффициента множественной регрессии:
Величина Rk подтверждает, что модель может использоваться для экономических расчетов.