9. По данным измерений /табл.2/ рассчитать основные характеристики ρ, ω 0, q параллельного контура и построить резонансную кривую тока I(ω).

Необходимые для построений величины можно рассчитать по выражениям, имеющимся в пояснениях к работе.

Сопротивление R₂ имеется в таблице, а сопротивление r₁ катушки в момент резонанса можно рассчитать или принять по результатам экспериментов с последовательным контуром.

Расчёт индуктивности Lк по каждому эксперименту выполняется как обычно:

Хк = ; Lк = Хк /ω; ρ = ,

ω ₀ = ; ω₀^’= ω ₀ ∙ ; b_1L= ; b_2С = ;

Q = = ,

где I_1L, I_2C -реактивные составляющие токов ветвей в момент резонанса.

Результаты исследования характеристик последовательного и параллельного резонансных контуров для наглядности свести в итоговую табл. 3.

Основные характеристики резонансных контуров Таблица 3.

Последовательный контур
ρ, Ом	ω 0,рад/с	ω С,рад/с	UC , В	ω L,рад/с	UL, В	Q	∆ = ω 2- ω 1

Параллельный контур

ρ = , Ом

ω 0= , рад/с

Q =

Вопросы и задания по лабораторной работе

1. Какие режимы в электрической цепи называют резонансными? Каким образом можно достичь резонансного режима?

2. При каких условиях в электрических цепях возникает резонанс напряжений и по каким признакам можно судить о его наступлении?

3. При каких условиях в электрических цепях возникает резонанс токов и по каким признакам можно судить о его наступлении?

4. Постройте резонансную кривую тока I (ω) и определите основные характеристики (ρ, ω₀, Q, ω _L, ω_C,) колебательного контура по рис.1, если Uвх= = 24В, f = var, R = 6 Ом, С = 26,54мкФ, L = 15,3 мГн.

5. В схеме по рис.4: Uвх = 24В, f = 50 Гц, R₁=10 Ом, Х₁ =17,32 Ом, сопро-тивление R₂ отсутствует. Определите необходимую ёмкость С конденсатора, чтобы в цепи наступил резонанс токов.

----------- АВХ. 25 октября 2009г.------------

Лабораторная работа № 6

ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

С ИНДУКТИВНО СВЯЗАННЫМИ ЭЛЕМЕНТАМИ

Цель работы: - экспериментально определить параметры реальных ка-тушек, имеющих индуктивную связь, найти их одноимённые зажимы и величину коэффициента связи;

- проверить расчетные соотношения, справедливые для последовательного и смешанного соединения элементов, а также для трансформаторной схемы.

Пояснения к работе

* Два элемента называют индуктивно связанными, если у них весь магнитный поток или его часть являются общими.

Кроме обычных r, x, z -параметров катушки в этом случае характеризу-ют взаимной индуктивностью М или сопротивлением Хм = wМ, или коэф-фициентом связи Ксв. Все эти величины можно рассчитать по данным первого или второго эксперимента лабораторной работы:

< 1.

* Два зажима двух индуктивно связанных катушек называются одноимён-ными (однополярными), если при одинаково направленных токах i₁, i₂ от-носительно этих зажимов магнитные потоки катушек складываются. Это так называемые «начала» и «концы» обмоток.

Одноимённые зажимы определяются экспериментально, для каждой пары катушек отдельно. В нашей лабораторной работе это можно сделать по результатам второго эксперимента, когда станут известны сопротивления при согласном Хсогл и при встречном Хвстр включении катушек.

* Индуктивно связанные катушки при последовательном соединении мо-гут оказывать друг на друга согласное или встречное влияние. Расчёт выполняется по закону Ома, с учётом знака сопротивления ±Хм :

;

;

* В цепях со смешанным соединением элементов, в трансформаторных схемах и в цепях с несколькими источниками энергии расчёты выполняются в комплексной форме либо по МЗК, либо, после «развязки» связи, по за-кону Ома.

Правило «развязки» связи: если катушки в узел соединены разноимёнными зажимами, то для эквивалентной замены связи в ветви катушек необходимо ввести элемент +Хм, а в общую для них ветвь - элемент -Хм. И наоборот. И это не зависит от принятых направлений токов в ветвях.

* В лабораторной работе исследуются индуктивно связанные элементы стенда со следующими ориентировочными параметрами: R₁ = 3.8 Ом, L₁ = 175 мГн, R₂ = 22 Ом, L₂ = 690 мГн, М = 240 мГн. В схеме со смешанным соединением элементов используются добавочные элементы стенда: R = 100 - 200 Ом, конденсаторы С = 10 - 20 мкФ. Входное напряжение Uвх = 30 В.

Домашняя подготовка к работе

1.Изучить тему «Цепи с индуктивно связанными элементами», познако-миться с целью и пояснениями к данной лабораторной работе. Подготовить схемы и таблицы, необходимые для выполнения экспериментов.

2. Расчёт выполнить цепи с последовательным соединением элементов, при согласном и встречном влиянии. Результаты расчёта внести в табл. 2.

Порядок выполнения работы

1. Собрать схему для определения параметров катушек – рис.1. Подклю-

ч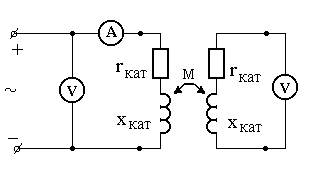 ая каждую из катушек к регулируемому источнику постоянного напряжения U₀ = 1-2 B, а затем к источнику синусоидального нап-ряжения U~10-20 B частотой 50 Гц, данные измерений занести в таблицу 1.

¬---------- Рис.1.

2. По измеренным величинам рассчитать и также внести в таблицу 1 сопротивления катушек, их взаимную индуктивность и коэффициент связи, за-писать параметры в комплексной форме.

,

Таблица 1. Экспериментальное определение параметров

индуктивно связанных катушек

* * *	U0, B	I0, A	U1, В	I1, A	U2x, B	Zk, Ом	Rk, Ом	Xk, Ом	Хм, Ом	М, мГн
1 катушка	0,8	0,2	15	0,272	20,5	55,1	4,0	55	75,4	240
2 катушка	2,2	0,1	24	0,111	8,34	216,2	22	216	75,1	239

3. Собрать схему по рис. 2 для проверки расчётных формул, справедливых для последовательного соединения индуктивно связанных реальных ка-тушек. На схеме разметка зажимов показана для встречного влияния катушек, но измерения следует выполнить как для согласного, так и для встречного включения катушек. Напряжение U_~ = 20-24 B, 50 Гц

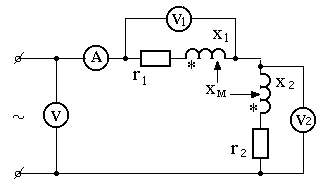
¬ Рис.2

Принимая rсогл = rвстр = r₁+ r₂ из первого эксперимента, по данным измерений вычислить индуктивные сопротивления Хсогл, Хвстр и значение взаимной индуктивности М .

; ; ;

Таблица 2.

Результаты исследования цепи при согласном и встречном

последовательном соединении катушек

Последовательное соединение		Uвх В	I, мA	U1, B	U2, B	Х, Ом
Согласное	Расчёт	24	56,9	7,42	16,61	421,8
	Эксперимент	24
Встречное	Расчёт	24	195	4,05	27,75	120,2
	Эксперимент	24

Сопоставить значения токов Iсогл и Iвстр в таблице 2 и сформулировать порядок определения одноимённых зажимов различных обмоток.

Далее исследование выполняется в двух вариантах:

Бригады с чётными номерами работают со схемой, представляющей сме-шанное соединение элементов (рис. 3); нечётные варианты исследуют транс-форматорную схему в режиме короткого замыкания (рис.4).

4а. Для чётных вариантов. Собрать схему цепи со смешанным соединением элементов. Резистор или конденсатор, добавляемый в схему, взять из блока пассивных элементов стенда. Измерения токов выполнить при напряжении Uвх = 30 В. Результаты измерений внести в табл.3.

Таблица вариантов схем со смешанным соединением

индуктивно связанных элементов

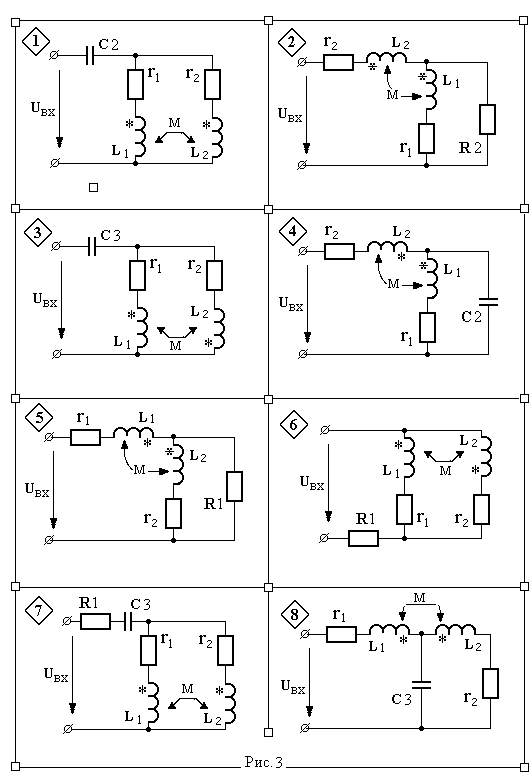
Таблица 3.

Расчётные и измеренные значения токов в схеме со смешанным

соединением индуктивно связанных элементов

Вариант 09	Uвх, B	I1, A	I2, A	I3, A	P2-1, Вт
Эксперимент	24				--
Расчёт	24	0,41	0,207	0,235	2,554

Домашний расчёт схемы с построением векторной диаграммы выполнить при оформлении отчёта.

4б. Для нечётных вариантов. Исследование трансформаторной схемы также выполняется сначала экспериментально, т.е. в лаборатории, а расчёт выполняется в домашних условиях при оформлении отчёта. Причём, расчёт выполняется по параметрам катушек, полученным в первом эксперименте работы. Расчёт следует закончить построением ВД трансформатора.

В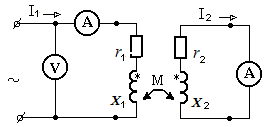 качестве примера рассмотрим расчёт трансформатора с параметрами:

Uвх = 24B, 50 Гц,

r₁ = 4 Ом , Х₁ = 55 Ом,

r₂ = 22 Ом, Х₂ = 216 Ом,

Хм = 75.4 Ом.

* Трансформатор описывается двумя уравнениями по II закону Кирхгофа:

Отсюда получаем выражения для расчёта токов:

А.

* Активная мощность, потребляемая трансформатором из сети:

Р₁ = Re Вт

Активная мощность, передаваемая через узел связи во вторичную обмотку

Р_1-2 = - Хм^. I₁∙ I2 ∙ sin (y₁ - y₂) =

= - 75,4^. 0.808^. 0,28 sin (-77,06 – [-71,244] ) = 1,732 Вт.

Таблица 4.

Результаты расчёта и измерений трансформаторной схемы

Трансформатор	U1, B	I1, A	P1, Вт	I2, A	Р1-2,Вт
Эксперимент	24		---		---
Расчёт	24	0,808	4,342	0,28	1.73

---------------------------- ♦ ---------------------------

Вопросы и задачи по лабораторной работе

1. В чём сущность явлений самоиндукции и взаимной индукции?

2. Как определяется знак напряжения взаимной индукции в уравнениях, со-ставляемых по II закону Кирхгофа? /правило знака слагаемого ±Zм Iq /.

3. Сформулируйте правила развязки связи и укажите, зачем она нужна и когда она целесообразна.

4. Поясните сущность «ёмкостного эффекта» в цепях с индуктивно связанными элементами. Возможен ли ёмкостный эффект в условиях третьего экспериментов лабораторной работы?

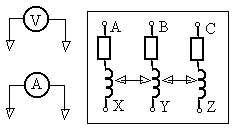
5. На рисунке показаны выводы обмо-ток трансформатора. Поясните, как определить одноимённые зажимы и взаим-ную индуктивность М обмоток тр-ра.

6. Поставлены три эксперимента, резу

л ьтаты которых указаны на схемах. Определите сопротивление Хм, укажите, согласно или встречно включены катушки в третьем эксперименте, разметьте зажимы катушек.

7. Каково условие передачи активной мощности через узел связи и чему равна мощность Рм_1-2 во втором эксперименте работы при встречном включении катушек?

8. Рассчитайте активную мощность Рм, передаваемую через узел связи в схеме со смешанным соединением индуктивно связанных катушек.

9. Определите входное сопротивление трансформаторной схемы, исследованной в лабораторной работе.

--------------------- ♦ ----------------------

Расчётно-лабораторная работа № 7

ИССЛЕДОВАНИЕ ЦЕПИ

ПРИ НЕСИНУСОИДАЛЬНОМ ВХОДНОМ НАПРЯЖЕНИИ

Цель работы: - проверка методики разложения в ряд Фурье пери-одических несинусоидальных функций и расчёта простых цепей при несинусоидальном входном напряжении.

Пояснения к работе

Методика расчёта линейных электрических цепей при несинусоидальных напряжениях или токах состоит в том, что заданное несинусоидальное воздействие представляют в виде гармонического ряда Фурье, расчёт цепи вы-полняют по каждой гармонике в отдельности, после чего записывают резуль-тирующие выражения мгновенных значений iнеsin, uнеsin, и находят действу-ющие значения величин Iнеsin Uнеsin.

[1]

Здесь А_1т sin(ωt+ψ₁) - первая гармоника, которую называют основной, так как она имеет период, равный периоду исследуемого сигнала. Ряд называется дискретным, так как все последующие гармоники ряда в целое число раз по частоте отличаются от основной. Раскрывая синусы суммы углов по каждой гармонике, получим запись ряда в более удобном виде, через синус-ные и косинусные составляющие с нулевыми начальными фазами:

[1а]

Если несинусоидальное напряжение или ток имеют типовую форму, то их представление рядом Фурье можно найти в учебнике или справочнике.

Если же несинусоидальная функция получена экспериментально, в виде осциллограммы, то её разложение в ряд Фурье выполняется графоаналитическим способом, по приближённым формулам, где интегралы заменяются конечными суммами слагаемых.

≈ = ;

Вк_т = ≈ ; [2]

Ск_т = ≈ ;

Через синусные и косинусные составляющие далее рассчитываются амплитуда и начальная фаза по каждой гармонике ряда:

ψк = arc tg [3]

В зависимости от требуемой точности разложения, период функции разбивают на n = 12- 24 -36 интервалов. Если функция обладает каким-либо ви-дом симметрии, то её разложение в ряд упрощается.

* При расчёте цепи несинусоидального тока следует помнить о том, что индуктивное и ёмкостное сопротивления зависят от частоты:

Х_L⁽⁰⁾ = 0, Х_L^(к) = К ∙Х_L⁽¹⁾ , Х_С⁽⁰⁾ = ∞, Х_L^(к) = Х_С⁽¹⁾/ к.

Из этого следует, что индуктивность подавляет высшие гармоники в кри-вой тока, делая её по форме близкой к виду первой гармоники подаваемого напряжения. Ёмкость, наоборот, способствует увеличению доли высших гармоник в кривой тока, чем делает её более искажённой в сравнении с кри-вой питающего напряжения.

Действующие значения несинусоидального тока и напряжения рассчитываются через действующие значения всех входящих гармоник, и не зави-сят от их начальных фаз:

; ; [4]

В лабораторной работе несинусоидальное входное напряжение получа-ют с помощью дросселя (катушка с ферросердечником). При подаче на дрос-сель синусоидального напряжения, ток (при насыщении сердечника) стано-вится несинусоидальным, и имеет сильно выраженную пикообразную фор-му. Напряжение, снимаемое с резистора R, повторяет эту форму кривой.

П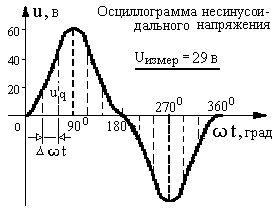 ример графоаналитического разложения несинусоидальной кривой

сложной формы в ряд Фурье.

Схема цепи для получения

несинусоидального напряжения

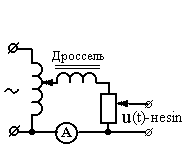
Как видим, полученная осциллограмма напряжения u(t) - это периодиче-ская несинусоидальная функция, симметричная относительно оси абсцисс и начала координат. Следовательно, при разложении в ряд кривая не будет содержать постоянной составляющей и чётных функций, и при этом достаточно будет исследовать лишь полупериод функции. Разбиваем его, напри-мер, на n = 6 равных интервалов с ∆ωt =30 ⁰, мгновенные значения напряжений uq(ωt) снимаем в конце каждого интервала. По формулам 2 рассчи-тываем коэффициенты ряда В_1т , С_1т для первой гармоники, В_3т , С_3т для третьей гармоники и т.д. Расчёты по каждой гармонике сводим в таблицы.

Таблица 1. Расчёт первой гармоники.

**	ωt, град	uq(ωt), B	uq·sinq(ωt)	uq·cosq(ωt)
1.	30	7,5	3,75	6,5
2.	60	25,5	22,08	12,75
3.	90	63,0	63,0	0
4.	120	32,1	27,8	-16,05
5.	150	8,0	4,0	-6,93
6.	180	0	0	0
= 40,21 B = - 1,243 B

По формулам [3] считаем амплитуду и начальную фазу первой гармони-ки. Величину угла ψк считаем с учётом знаков sin и cos - составляющих:

= 40,23 В = -1,77 ⁰.

Таблица 2. Расчёт третьей гармоники.

**	ωt, град	uq(ωt), B	uq·sinq(3ωt)	uq·cosq(3ωt)
1.	90	7,5	7,5	0
2.	180	25,5	0	-25,5
3.	270	63,0	-63	0
4.	360	32,1	0	32,1
5.	450	8,0	8,0	0
6.	540	0	0	0
= -15,83 B = + 2,2 B

= 15,982 В = +172,1 ⁰.

Итак, выражение несинусоидального напряжения, рассчитанного с точ-ностью до 3-ей гармоники, будет:

(5)

Чтобы убедиться в правильности выполненного разложения, рассчитаем действующее значение напряжения и построим расчётную кривую напряжения, сравнив их с полученными экспериментально.

.

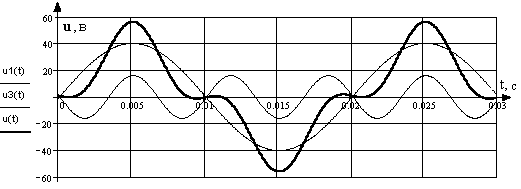Расчётный график входного напряжения u(t) .

Обратим внимание на следующее: первая и третья гармоники сдвинуты почти на 180⁰, т.е. находятся почти в противофазе. Именно в таком случае несинусоидальная функция получается пикообразной. В противном случае несинусоидальная кривая получается уплощённой.

Подготовка к работе и порядок выполнения

1. В домашней подготовке к работе необходимо изучить тему «Электри-ческие цепи при несинусоидальных ЭДС и токах». Вычертить схему источ-ника несинусоидального напряжения, подготовить таблицы для расчёта 1,3 и 5-ой гармоник и формулы для их расчёта.

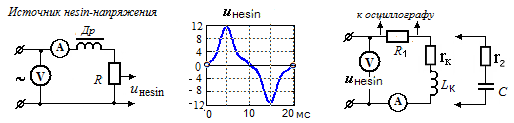
2. В лаборатории собрать схему с источником несинусоидального напря-жения. На вход источника подать синусоидальное напряжение частотой 50 Гц от одной из фаз 3х-фазного источника, имеющегося на стенде. В качестве ре-зистора R, с которого снимается несинусоидальное напряжение, сформиро-вать (параллельным соединением) сопротивление 20-25 Ом.

3. Из съёмных элементов стенда, в соответствии с вариантом, сформировать исследуемые RL и RС-нагрузки.

Таблица 1. Варианты нагрузки

Параметры	1 вариант	2 вариант	3 вариант	4 вариант
R1, Ом	51	51	51	51
rк, Ом	4	52	4.5	22
L, мГн	175	100	120	0.69
rС, Ом	200	75	150	100
С, мкФ	20	10	15	20

4. Регулируя питающее напряжение, добиться на осциллографе кривой

входного несинусоидального напряжения uнеsin c параметрами, близкими к изображённым на рисунке. Записать масштабы по напряжению m_u и по вре-мени m_t, определяемые положением переключателей осциллографа, и снять кривую с экрана осциллографа для домашней обработки. Измерить и внес-ти в табл. 2 действующее значение напряжения (Uнеsin ≈ 5-10В).

5. Подключая RL, а затем RС- нагрузку, измерить действующие значения токов I_RL и I_RС. Измеренные величины также внести в табл. 2.

Таблица 2. Амплитуды гармоник входного неsin-напряжения.

Действующие значения напряжения и токов нагрузки

Исследуемые величины	Um(1), B	Um(3), B	Uнеsin, B	IRL, мА	IRС, мА
Эксперимент	---	---
Расчёт	7.9	3.33	6.06	73.1	23.9

6. Подключая осциллограф к резисторам R₁ и r₂, визуально сравнить кривые токов i_RL и i_RC и сделать вывод о влиянии индуктивности и ёмкости на форму кривой тока.

7. При оформлении отчёта обработать осциллограмму входного напряжения uнеsin , найти амплитуды гармоник Um⁽¹⁾ и Um⁽³⁾, и заполнить расчётную часть табл.2. Сделать выводы по работе.

Вопросы и задания по лабораторной работе

1. Почему в лабораторной работе при разложении осциллограммы в ряд Фурье не рассчитывали нулевую и вторую гармоники?

2. Какое значение несинусоидального тока измеряет амперметр магнито-электрической системы? Рассчитайте это значение, если i = 4sin(ωt) -2 sin(3ωt).

3. Какие значения несинусоидального напряжения измеряют вольтметры электромагнитной и электродинамической систем? Рассчитайте показание электромагнитного амперметра, если i = 4sin(ωt) - 2 sin(3ωt).

4. Как изменяется индуктивное и ёмкостное сопротивление току разных гармоник?

5. Сопротивление цепи для токов 5^й гармоники: Z⁽⁵⁾ = 10 - j10 Ом. Определите сопротивление цепи для токов 2^й гармоники.

6. Определите действующее значение несинусоидального напряжения u(t) = 100 +200 sin(ωt - 30⁰) - 100 sin(3ωt + 45⁰) В.

7. Как влияют индуктивность и ёмкость на форму кривой несинусоидального тока в сравнении с кривой напряжения?

--------------------- ■ ---------------------

Расчётно-лабораторная работа № 8

ИССЛЕДОВАНИЕ пассивного ЧЕТЫРЕХПОЛЮСНИКА

Цель работы: определить характеризующие 4-полюсник коэффициенты и передаточные W(jω) функции. Составить схему замещения 4-полюс­ника.

Пояснения к работе

Четырехполюсником называют электрическую цепь или её часть любой конфигурации, у которой выделены два входных и два выходных зажима.

Четырехполюсник можно характеризовать А, В, С, D - коэффициентами (первичные параметры), характеристическими (волновыми) параметрами Zc, g = а+jb и передаточными функциями W(jω) по напряжению и по току.

Уравнения, связывающие напряжения и токи на входе и выходе 4-полюс-ника (как симметричного, так и несимметричного), при любой нагрузке, записанные в А-форме, имеют вид:

│ ;

│ ; (1)

А, В, С, D - комплексные коэффициенты, характеризующие 4-полюсник на данной частоте. У линейных пассивных четырёхполюсников они подчиня-ются соотношению: (2)

Коэффициенты 4-полюсника могут быть определены непосредственно по его схеме и заданным параметрам или по данным опытов ХХ и КЗ:

А = ; В = А∙Z_2к; . (3)

Здесь Z_1Х, Z_2Х - комплексы входного сопротивления четырехполюсника в режиме холостого хода относительно входных и выходных зажимов; Z_2К - комплекс входного сопротивления четырехполюсника относительно выход-ных зажимов, когда входные зажимы замкнуты накоротко.

У симметричного четырёхполюсника: Z_1Х = Z_2Х = Z_ХХ, Z_1К= Z_2К = Z_КЗ и

равны коэффициенты А = D.

Если схема четырёхполюсника неизвестна, его А,В,С,D- коэффициенты могут быть рассчитаны по данным соответствующих опытов ХХ и КЗ.

Для исследования различных режимов работы 4-полюсника обычно пользуются трёхэлементными Т- и П- схемами замещения, параметры которых находят по следующим выражениям:

Т- схема: ; (4)

П- схема: (5)

Если 4-полюсник представляет собой стандартную Т- или П- схему, то его АВСD- коэффициенты проще найти из соотношений (4 или 5).

* Характеристические параметры 4-полюсника. Если устройства, пред-ставляемые четырёхполюсниками, работают в широком диапазоне частот (усилители, электрические фильтры, длинные линии), удобнее пользоваться характеристическими (волновыми) параметрами 4-полюсника:

Z_С1, Z_С2 - характеристические сопротивления несимметричного 4-полюс-ника со стороны входных и со стороны выходных зажимов;

g = а + jb - постоянная передачи 4-полюсника, безразмерная величина, характеризующая передачу сигнала по мощности в логарифмическом масштабе: g = а+jb = ½ ℓп = ½ ℓп , (6)

причём, по модулю: а = ½ ℓп = ½ ℓп , Нп.

а - коэффициент затухания (ослабления) сигнала по мощности в неперах [Нп], белах [Б ] или децибелах [дБ ].

1 Нп = 8.686 дБ, 1 дБ = 0.115 Нп.

b - коэффициент изменения фазы “мощностного” сигнала при прохождении через четырёхполюсник:

b = ½ [(ψu1 - ψu2) + (ψ_i1 - ψ_i2)], рад.

Уравнения симметричного 4-полюсника в А-форме, записанные через его волновые параметры, имеют вид:

│U₁ = U₂ ch g + Zc∙I₂ sh g;

│I ₁ = U₂ (sh g /Zc) + I₂ ch g; (1a)

Характеристические параметры 4-полюсника могут быть рассчитаны через АВСD-коэффициенты или непосредственно по данным опытов ХХ и КЗ.

(7)

g = а + jb .

По данным опытов холостого хода и короткого замыкания:

(8)

.

* Рассмотренные АВСD-коэффициенты и волновые параметры Z_C и g = а + jb характеризуют непосредственно сам 4-полюсник. При подключении не-согласованной нагрузки общее затухание сигнала изменится. Чтобы охарак-теризовать передачу сигнала при произвольной нагрузке, пользуются понятием коэффициентов передачи по напряжению Кu и по току Кi, или в общем случае – передаточными функциями W(jω).

К_u = = ; К_i = = ; (9)

В лабораторной работе в качестве нагрузки используется резистор Rнг = 100 Ом.