
- •Методические указания
- •Часть I
- •Исследование сложной цепи постоянного тока
- •Порядок выполнения второй части работы
- •Проверка соотношений при параллельном соединении элементов
- •3. Включить двухполюсники параллельно и произвести измерения величин, указанных в табл.2. Токи ветвей Iкат, irc принять из таблицы 1.
- •Проверка соотношений последовательного соединения
- •4. Собрать схему цепи с последовательным соединением двухполюсни-ков и произвести измерения величин, указанных в табл.3.
- •Вопросы и задания по лабораторной работе
- •Таким образом, о наступлении резонанса напряжений можно судить по наибольшему току в цепи, а уточнять - по показанию ваттметра, сравнивая его с произведением показаний амперметра и вольтметра.
- •Порядок выполнения работы
- •9. По данным измерений /табл.2/ рассчитать основные характеристики ρ, ω 0, q параллельного контура и построить резонансную кривую тока I(ω).
- •Домашняя подготовка к работе
- •Подготовка к работе и порядок выполнения
- •Вопросы и задания по лабораторной работе
- •Часть I
Таким образом, о наступлении резонанса напряжений можно судить по наибольшему току в цепи, а уточнять - по показанию ваттметра, сравнивая его с произведением показаний амперметра и вольтметра.
* В момент резонанса, в случае, если ХL = ХС > R, напряжения на индуктив-ности и на ёмкости могут значительно превышать напряжение источника:
UL0 = UС0 = Х0∙ I = ρ∙ I > Uвх = Zвх∙ I = R∙ I .
Отношение напряжений на реактивных элементах при резонансе к напряжению источника называют добротностью контура Q. Добротность контура Q можно рассматривать и просто как соотношение параметров контура.
Q
=
![]() =
=
![]() =
=
![]() ;
[4]
;
[4]
* Полоса
пропускания контура определяется по
кривой тока I(ω),
на уров-не
0.707 Iмакс,
так как именно при
таком снижении тока мощность (энергия)
в реактивных элементах контура
уменьшается вдвое. Типовой
вид резонансных кривых последовательного
кон-тура и выражения его частотных
характеристик приведены
на рис.2.
Полоса
пропускания контура определяется по
кривой тока I(ω),
на уров-не
0.707 Iмакс,
так как именно при
таком снижении тока мощность (энергия)
в реактивных элементах контура
уменьшается вдвое. Типовой
вид резонансных кривых последовательного
кон-тура и выражения его частотных
характеристик приведены
на рис.2.
I(ω)
=![]() ;
;
UL (ω) = ХL(ω)∙I(ω);
UС (ω) = ХС(ω)∙I(ω).
Рис.2. Резонансные кривые последовательного контура
Заметим, что на резонансной частоте напряжения UL и UС равны, но их максимумы имеют место при частотах отличных от резонансной.
ωС
=ω0
∙![]() <
ω0,
ωL
= ω0
∙
<
ω0,
ωL
= ω0
∙
![]() > ω0.
[5]
> ω0.
[5]
Необходимо также отметить, что все приведенные характеристики зависят от соотношения R, L, С-параметров контура, т.е. от добротности Q, которая может достигать значений Q макс = 100 -250.

Чем больше добротность контура, тем ос-трее резонансные кривые контура, тем лучше «настройка» контура на определённую частоту. При добротность Q ≤ 1 все кривые становятся весьма пологими.
В лабораторной работе при исследовании характеристик последовательного контура выполняются два эксперимента: при I макс = 2,5 А и при I макс = 1,4 А.
Рис.3. Резонансная кривая тока I(ω) при различной добротности контура.
ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР
РЕЗОНАНС ТОКОВ
Характеристики идеального и реального контуров существенно отличаются. Для контура с идеальными L и C элементами волновое сопротивление и резонансная частота определяются такими же выражениями, как и для последовательного контура:
ρ = ; ω0 = . [6]
В лабораторной работе сопротивления r1 катушки и r2 в RC-двухполюс-нике существенны, ими нельзя пренебречь. Резонансная частота такого кон-тура и его частотные характеристики определяются выражениями:
ω 0′=
∙
0′=
∙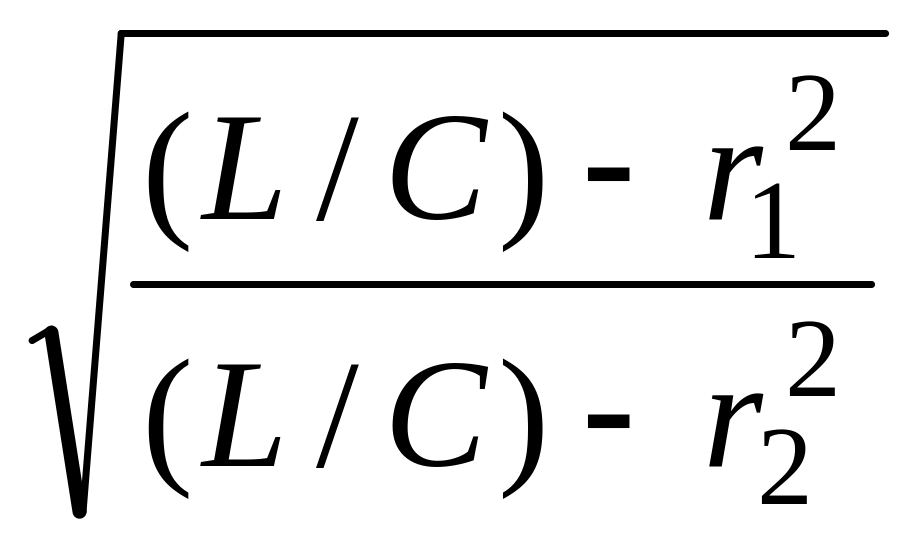 =
ω0∙
=
ω0∙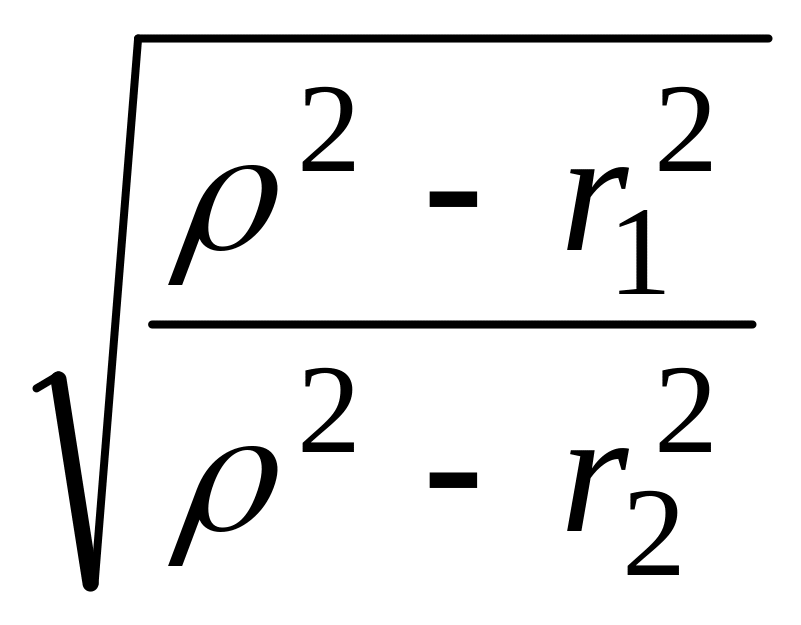 ;
[6а]
;
[6а]
b1L
=![]() ;
b2С
=
;
b2С
=![]() ;
;
Рис.4. Схема реального параллельного контура
Из выражений [1а] следует, что резонанс токов возможен лишь в случаях, когда сопротивления r1 и r2 оба больше или оба меньше волнового сопротив-ления ρ. На рис.5 представлен типовой вид резонансных кривых Iвх(ω), I1L(ω), I2C(ω) параллельного контура, приведены расчётные формулы.
Iвх(ω)
= у
∙U
=![]() ∙U
; [7]
∙U
; [7]
I1L = b2L∙U = ∙ U ; I2C = b2С∙U = ∙ U.

 Рис.5.
Резонансные
кривые паралл. к
Рис.5.
Резонансные
кривые паралл. к
В этом случае при резонансе равными по величине становятся реактивные составляющие токов I1 и I2. Полные токи (из-за неравенства составля-ющих I1а, I2а) могут быть и не равны между собой, но они могут значите-льно превышать общий ток цепи, который в этот момент будет наименьшим:
I вх = (g1+g2)∙U.
Таким образом, для параллельного контура признаками наступления резонанса токов будут наименьший общий ток цепи I и показание ватт-метра Рw, которое должно быть равно произведению Uвх∙I вх , поскольку в момент резонанса cos φ = 1.
* Вид кривой Iвх(ω) зависит также от добротности контура, которая у па-раллельного контура определяется как отношение проводимостей:
Q
=
![]() .
[8]
.
[8]
*
Избирательность контура по кривой тока
определяется как ширина полосы
пропускания контура на уровне
I
=![]() Iмin:
Δ
= f
2 -
f
1
.
Iмin:
Δ
= f
2 -
f
1
.
