1.2.2. Динамические звенья систем автоматического управления
По теории системы автоматического управления и регулированию существует обширная библиография. В рамках данного раздела даются только минимальный состав основных терминов и понятий из этой области. Изложение ведется согласно источнику [5].
А. Структурные схемы автоматики
Динамические звенья. Для анализа и моделирования систем автоматического управления производят их разбиение на отдельные элементы. При этом элементы не обязательно должны представлять отдельные устройства. Основной принцип выделения – возможность описать поведение выделенного элемента уравнением определенного типа. Такой выделенный элемент принято называть динамическим звеном, его условное изображение дано на рис. 33. Ограничимся рассмотрением динамических звеньев, имеющих одну входную X(t) и одну выходную Y(t) величину. При этом будет предполагать у звеньев однонаправленность действия, т.е. способность передавать воздействие только в одном направлении от входа к выходу.
Рис.33. Динамическое звено
Входная и выходная величина могут описываться различным образом. При рассмотрении процессов во временной области эти величины представляют собой функции времени, а уравнение, их связывающее, в общем случае является дифференциальным уравнением. Звено может быть линейным и нелинейным. В случае нелинейных звеньев принято их линеаризировать в области малых изменений, т.е. заменять их приближенно некоторым линейным звеном, поведение которого достаточно близко к поведению исходного звена.
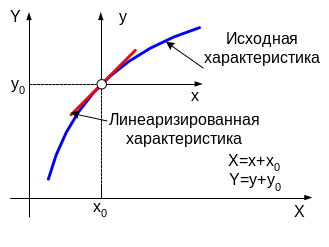
При этом необходимо помнить, что достаточно точные результаты возможны только в области малых изменений входной X и выходной Y величин от некоторого исходного состояния (x0, y0), для которого выполнена линеаризация. В качестве исходного состояния чаще всего выбирают установившийся режим. Таким образом, мы ограничимся рассмотрением линейных динамических звеньев.
Частным случаем систем автоматического управления являются системы автоматического регулирования. В пределах данного подраздела будем рассматривать системы автоматического регулирования. Автоматическое регулирование – изменение какой либо физической величины по требуемому закону без непосредственного участия человека. Целью управления в этом случае является обеспечение требуемого закона изменения регулируемой величины. На рис. 34 приведена схема регулятора с обратной связью. Наиболее распространены регуляторы, использующие принцип регулирования по отклонению между задаваемым значением величины Z и ее фактическим значением Y. Это отклонение приято называть ошибкой X. Зависимость регулирующего воздействия U от сигнала ошибки X без учета инерционности регулятора называют законом регулирования. Поскольку для вычисления ошибки приходится подавать выходной сигнал на вход системы, то получается замкнутая система управления.
Рис. 34. Схема регулятора с обратной связью
Описание динамических звеньев. Во временной области динамическое звено может быть описано дифференциальным уравнением с постоянными коэффициентами.
……
……+
.
Часто используется символический метод записи линейных дифференциальных уравнений, при этом в отечественной литературе вводятся следующие обозначения
Тогда дифференциальное уравнение звена может быть представлено в алгеброаизированной форме
Кроме временной области широко
используется отображение в области
комплексной переменной с использованием
операторного преобразования Лапласа
£. Вводится
комплексная переменная, обозначаемая
в отечественной литературе
и находится изображение функций Y
и X по формулам:
£
y(t)
£
x(t)
Для динамического звена при использовании изображений функций вводится понятие передаточная функция звена – отношение изображения выходной функции к изображению входной, при условии, что все изображения получены при нулевых начальных условиях
Описание динамического звена в операторной форме будет выглядеть следующим образом
Нетрудно заметить, что запись в операторной форме по структуре совпадает с алгебраизированной формой записи дифференциального уравнения звена.
Если для полинома, находящихся в числителе передаточной функции найти корни, называемые нулями функции p00, …, p0m и найти корни полинома знаменателя (полюса функции) p0, …, pn, то передаточную функцию можно записать в следующем виде
.
Здесь
- характеристическое уравнение системы.
Отметим, что символы, используемые для обозначения операторной и алгебраизированной форм записи, в иностранной литературе могут использоваться в противоположном значении.
Структурная схема. Для отображения и анализа систем автоматического управления применяется структурные схемы, которые выполняются по определенным правилам.
Структурной схемой системы автоматического управления (регулирования) называется схема, показывающая из каких звеньев состоит это устройство, и как эти звенья соединены между собой.
Элемент структурной схемы изображают в виде прямоугольника, в котором указывают обычно его передаточную функцию. Входные и выходные величины представляются в виде сигналов. Связи между элементами обладают однонаправленным действием. Такие правила позволяют отображать в наглядном виде достаточно сложные автоматические системы. Для сигналов вводят некоторые математические операции, для которых используют специальные графические обозначения. Такая форма представления используется и в интерфейсах многих программ, позволяющих анализировать автоматические системы.
Рис.35. Изображение динамического звена в структурной схема
Передаточные функции системы с обратной связью. Рассмотрим структурную схему регулятора, показанного на рис.34. Представим на рис. 36 устройство управления и объект управления в виде одного динамического звена с передаточной функцией W(p)
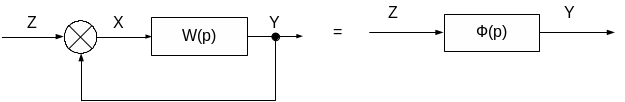
Рис. 36. Структурная схема регулируемой системы
а - с обратной связью, б – в виде одного звена
Передаточная функция разомкнутой системы по ошибке
;
передаточная функция замкнутой системы по воздействию
С учетом того, что X=Z-Y получаем передаточные функции замкнутой системы по заданию и по ошибке
; 
Правила преобразования структурных схем. Правила преобразования структурных схем позволяют упростить сложные схемы и получить более наглядное их отображение. Правила проиллюстрируем путем изображения эквивалентных схем.
Параллельное соединение звеньев, на примере пропорционально-интегрального регулятора (PI-регулятора)
Звено
с обратной связью:
Перенос звена из обратной связи. W-1(p) функция, обратная W(p),
W-1(p) = 1 / W(p)
Последовательное соединение динамических звеньев
Типовые воздействия. При анализе регуляторов и систем управление их поведение принято рассматривать при различных стандартизированных (типизированных) воздействиях. Ниже приведены наиболее часто применяемые воздействия.
1(t) – единичная функция, приложенная в момент времени 0
:
1(t-t0) – единичная функция, приложенная в момент времени t0
Дельта (Δ) - функция, приложенная в момент времени 0:
δ(t)
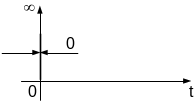
Дельта (Δ) - функция, приложенная в момент времени t0: δ(t-t0):
-
производная от единичной функции даёт
δ-функцию.
Гармоническая функция
