62. О методах полного прогноза с кубической скоростью

Пусть x^* - точное решение, {x_k}→ x^* , тогда говорят, что метод сх-ся со скоростью , если , 0<q<1. Если =1, то скорость линейная, =2 – квадратичная, =3 – кубическая.

В мет неполн прогн исп-ся , а в мет полн прогноза используется . Дост-ва: «разболтка» наступает на 1-2 порядка позже, чем в методах второго порядка (методы 2 порядка позв. получить решение с точностью до по норме невязки, а методы третьего порядка - ). Недостатки: 1) узкая область сх-ти (меньше, чем область сх-ти в методах с квадратичной скоростью); 2) сложнее программируется, занимает > памяти под дополн вектора.

Буд гов, что ф-ция f:XY диф-ма по Фреше в точке x₀X, если сущ-т лин огран. оператор Df(x₀)L(V,Y), для кот вып-ся усл. ||f(x₀+h) ‑ f(x₀)- Df(x₀)h||_Y=o(||h||_V),где || || _Y – норма в пр-ве Y,||.||_V – норма в векторном пр-ве V, параллельном пр-ву X.

(1)

Шаг1.Решается 1-ое ЛУ (3)

Шаг2.2-ое ЛУ (4)

Шаг3. Вносится поправка в : (5)

Шаг4. Если то конец просчётов, иначе переход на шаг 5.

Шаг5. Если то иначе

(**)

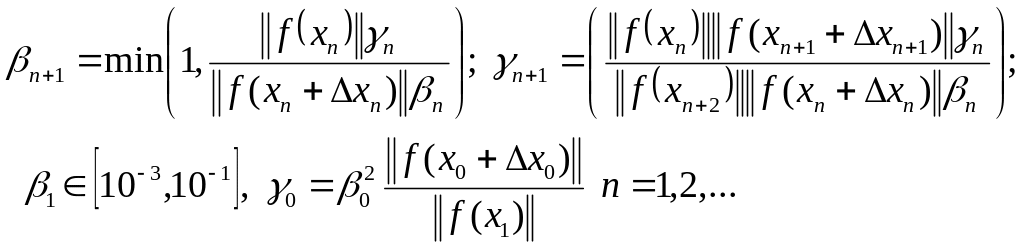Теорема. Пусть -решение уравнения (1) существует и выполняются следующие условия: а) б) в) г) (*). Тогда итер процесс (3)-(5) со сверхлин скор сход к . Оценки погр n-го прибл-я имеет вид .

Док-во. (6)

С учетом (4), . (7)

Оц-м и .Исп теор о среднем: , (8). откуда в силу (3), (8) ; (9)

Здесь . Далее, из (4), (9) имеем:

(10)

Подстановка (9), (10) в соотношение (7) : (11)

Пусть и , тогда (11) выглядит (12)

. Тогда (13). Пусть , тогда , тогда , след в силу (13) . Отсюда . Тогда . Т.о., монотонно возрастает, а - монотонно убывает с ростом n. , из которой следует слабая сходимость элементов , генерируемых алгоритмом (2)-(5), к .

Радиус сферы определяем стандартным образом.

Индукт пол оц-ки

_{Оцениваем по у и выбираем максимальное.}

Переход к пределу в последнем неравенстве при n позволяет утверждать, что все последовательные приближения не выходят за пределы сферы .

63. Неполный прогноз куб скорость непрер оператор

- раздел разность 1ого поряд.

- раздел разность 2–ого порядка.

Аналог интерполяц. формулы Ньютона для операторов:

(1)

₍₂₎

Шаг 1. , где . (3)

Шаг 2. ₍₄₎

Шаг 3. . (5)

Шаг 4. ₍₆₎

Шаг 5. Если – конец просчетов, иначе – переход на шаг 6.

Шаг 6. Если , то , иначе пересчет шаговой длины по формуле .

Теорема. Пусть в области , существует -решение уравнения f(x)=0 и выполняются следующие условия: 1) 2) 3) .

Тогда итерационный процесс (2)-(6) со сверхлинейной сходится к . Оценки погрешности ; .

Док-во.

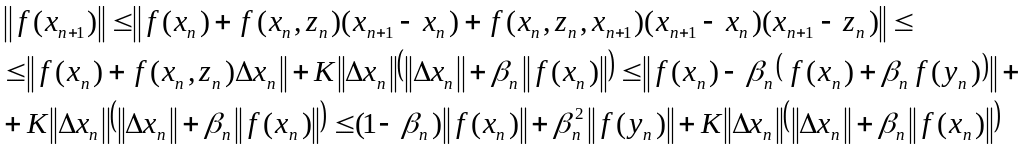
Оценим :

О ценим :

где _.Возвращаемся к оценке :

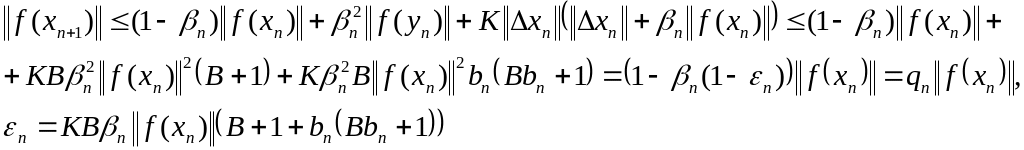
.Тогда (14)

Пусть , тогда , тогда , в этом случае в силу (14) .

Отсюда следует, что . Тогда

Т о, монотонно возрастает, а - монотонно убывает с ростом n. ,

Радиус сферы

Индуктивно получ оценки

Оцениваем по у и находим максимум.

Перейдем к пределу в посл нер-ве, след все посл-ные прибл .

, что невоз в силу шага 5.

Замеч. Лок квадратичная скорость сх-ти процесса следует из (*) при _n=1.