53. Нелокальные одношаговые итер процессы неполного прогноза для решения нелинейных уравнений с гладкими операторами.

Опр: Будем говорить, что ф-ция f:XY дифф-ма по Фреше в т-ке x₀X, если сущ-ет лин огранич оператор Df(x₀)L(V,Y), для которого выполн условие: ||f(x₀+h) ‑ f(x₀)- Df(x₀)h||_Y=o(||h||_V), где || || _Y – норма в пр-ве Y, || || _V – норма в векторном пр-ве V, параллельном пр-ву X.

Дост-ва классич метода Ньютона: простота и быстрая квадратичная сх-ть.Недостаток: зав-ть сход-ти от нач приближения х[0] .

В методах неполного прогноза при выч-нии исп-ся норма , а в методах полного прогноза используется .

(1)

Шаг1. Решается лин ур-ние отн-но : (3)

Шаг2. Вносится поправка в : (4)

Шаг3. Если где -малая вел-на, то выход, иначе переход на 4

Шаг4. Опр-ся новая шаговая длина: если то иначе

Теорема. Пусть в области , сущ -решение ур-ния f(x)=0 и выполн след условия: а) б) в) г) , тогда итер процесс (3), (4) со сверхлин скоростью (локально с квадратичной) сход к . Оценки погрешности .

Док-во.

. Тогда (5)

Пусть , тогда , тогда , в этом случае в силу (5) . Отсюда следует, что . Тогда . Т о, посл-ть монот возрастает, а - монотонно убывает с ростом n. Индуктивные рассуждения позволяют получить оценку , из кот следует слабая сх-ть эл-тов , генерируемых алг-мом (2)-(4), к . (6)

Определим радиус сферы

Получим .

Покажем, что достигнет 1:

, что невозм в силу шага 4.

, если альфа=1 –лин сход-ть, =2 – квадратичная.

Замечание Локальная квадр скорость сходимости следует из (5) при _n=1.

54. Нелокальные многошаговые итер проц неполного прогноза для решения нелинейных уравнений с гладкими операторами.

Опр: Будем говорить, что ф-ция f:XY дифф-ма по Фреше в т-ке x₀X, если сущ-ет лин огранич оператор Df(x₀)L(V,Y), для которого выполн условие: ||f(x₀+h) ‑ f(x₀)- Df(x₀)h||_Y=o(||h||_V), где || || _Y – норма в пр-ве Y, || || _V – норма в векторном пр-ве V, параллельном пр-ву X.

В одношаговых м-дах исп-ся нормы , а в многошаговых в 3-х: . В методах неполного прогноза при выч-нии исп-ся норма , в м-дах полного прогноза исп-ся .

(1)

Шаг1. Решается лин ур-ние отн-но : (3)

Шаг2. Вносится поправка в : (4)

Шаг3. Если где -малая вел-на, то выход, иначе переход на 4

Шаг4. Опр-ся новая шаговая длина: если то иначе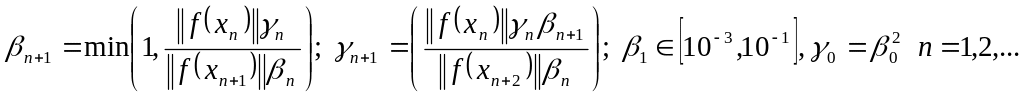

Теорема. Пусть в области , сущ -решение ур-ния f(x)=0 и выполн след условия: а) б) в) г) , тогда итер процесс (3), (4) со сверхлин скоростью (локально с квадратичной) сход к . Оценки погрешности .

Док-во.

.Тогда (5)

Пусть , тогда , тогда , в этом случае в силу (5) , Отсюда следует, что . Тогда .

Т о, посл-ть монот возрастает, а - монотонно убывает с ростом n. Индуктивные рассуждения позволяют получить оценку , из кот следует слабая сх-ть эл-тов , генерируемых алг-мом (2)-(4), к . (6)

Определим радиус сферы

Получим .

Покажем, что достигнет 1:

, что невозм в силу шага 4.

, если альфа=1 –лин сход-ть, =2 – квадратичная.

Замеч Локальная квадр скорость сходимости следует из (5) при _n=1.