Решение

Уравнение представляет собой плоскость, отсекающую на осях отрезки, равные 1; x = 0, y = 0, z = 0 - координатные плоскости. Область есть пирамида (рис. 2.3).

> with(plots):

> with(student):

> A1:=plot3d([(u),(v),(1-u-v)],u=0..1,v=0..1,axes=normal):

> A2:=plot3d([(0),(u),(v)],u=0..1,v=0..1-u,axes=normal):

> A3:=plot3d([(u),(0),(v)],u=0..1,v=0..1-u,axes=normal):

> A4:=plot3d([(u),(v),(0)],u=0..1,v=0..1-u,axes=normal):

> display({A1,A2,A3,A4},labels=[x,y,z],scaling=constrained,view = [0 .. 1.25, 0 .. 1.25, 0 .. 1.25]);

И проекция, получаемая из исходного рисунка, соответствующим поворотом (справа):

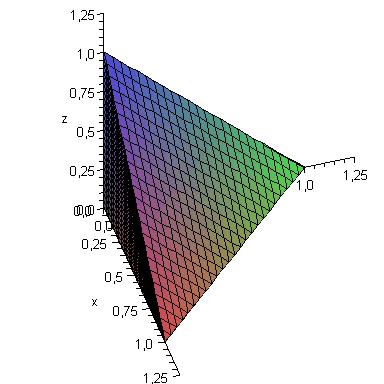
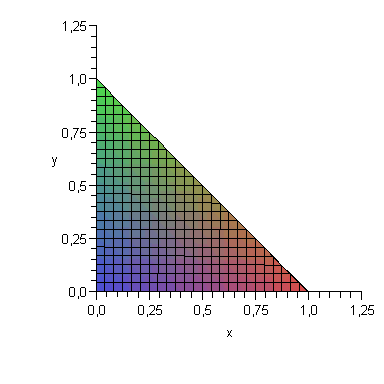
Рисунок. 2.3

Из чертежа сразу видно, что по любой из переменных можно с одинаковым успехом брать постоянные пределы, и они равны 0 и 1. Возьмем, например, постоянные пределы по . Проекцией пирамиды на плоскость является треугольник, ограниченный прямыми . Отсюда определяем пределы интегрирования по . Для переменной нижним пределом интегрирования будет, очевидно, (плоскость ), а верхним – значение , полученное из уравнения плоскости , т.е. . Определив пределы интегрирования по каждой из переменных, можем представить данный тройной интеграл через повторный и выполнить вычисления, последовательно вычисляя соответствующие определенные интегралы. Получим:

= =

= = =

= = =

= = = – .

Вычисление интеграла в Maple происходит следующим образом:

> with(student):

> Tripleint(1/(1+x+y+z)^3, z=0..1-x-y, y=0..1-x, x=0..1);

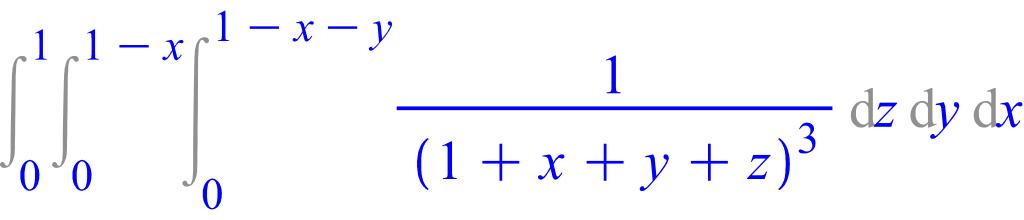
> value(%);

Пример 2. Вычислить: , где тело ограничено поверхностями x = 2, y = , y = 0, z = 0, z = 2.

Решение

Выполним рисунок области интегрирования, ограниченной заданными в условии плоскостями (рис. 2.4).

В пакете Maple методика построения имеет следующий вид:

> with(plots):

> with(student):

> A1:=plot3d([(u),(v),(2)],u=0..2,v=0..u/2,axes=normal):

> A2:=plot3d([(u),(v),(0)],u=0..2,v=0..u/2,axes=normal):

> A3:=plot3d([(2),(v),(u)],u=0..2,v=0..1,axes=normal):

> A4:=plot3d([(u),(u/2),(v)],u=0..2,v=0..2,axes=normal):

> A5:=plot3d([(u),(0),(v)],u=0..2,v=0..2,axes=normal):

> display({A1,A2,A3,A4,A5},labels=[x,y,z],scaling=constrained);

Рисунок. 2.4

Проекция строится следующим образом:

> inequal({y<x/2,x=2,y=0},x=0..2,y=0..1,optionsfeasible=(color=

blue),optionsexcluded=(color=white),axes=normal,labels=[x,y],

scaling=CONSTRAINED);

Рисунок. 2.5

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области (V) на выбранную плоскость изображена на рис. 2.5. Тогда исходный интеграл сводится к повторному с пределами интегрирования (рис. 2.5) по переменной х от 0 до 2, по у от 0 до , и, в соответствии с рис. 1, по оси z от 0 до 2.

= = =

= 2 = 2 = 2 = 2сh =

= 2(ch2 – 1).

Вычисление интеграла в Maple происходит следующим образом:

> with(student):

> Tripleint((x^2)*cosh(x*y), z=0..2, y=0..x/2, x=0..2);

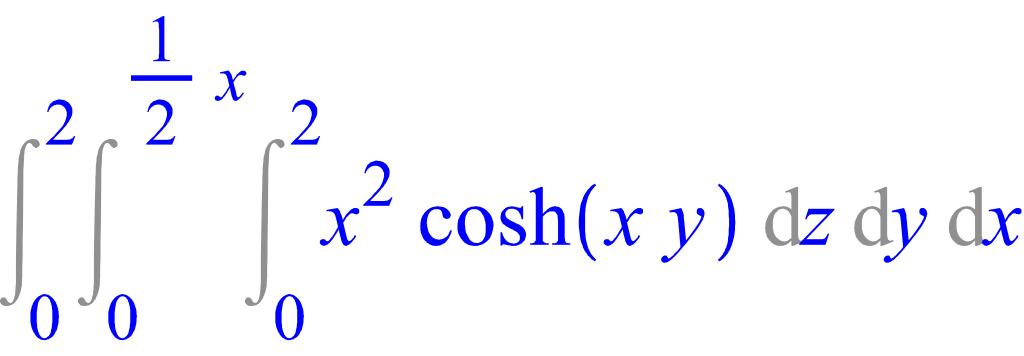
> value(%);

Пример 3. Вычислить: , где тело (V) ограничено поверхностями x = 2, y = 2x, y = 0, z = 0, z = xy.