1.6.2. Вычисление площадей поверхностей
ПРИМЕР 1.
Вычислить площадь той части плоскости
,
которая заключена в первом октанте
(рис.1.21).
> with(plots):
> with(student):
> A1:=plot3d([(u),(v),(6-(3/2)*v-3*u)],u=0..4,v=0..4,axes=normal):
> A2:=plot3d([(u),(-sqrt(4*u-u^2)),(v)],u=0..4,v=u..2*u,axes=normal):
> A3:=plot3d([(u),(v),(u)],u=0..4,v=-sqrt(4*u-u^2)..sqrt(4*u-u^2),axes=normal):
> A4:=plot3d([(u),(v),(2*u)],u=0..4,v=-sqrt(4*u-u^2)..sqrt(4*u-u^2),axes=normal):
> display({A1},labels=[x,y,z],scaling=constrained,view = [0 .. 3, 0 .. 5, 0 .. 7]);
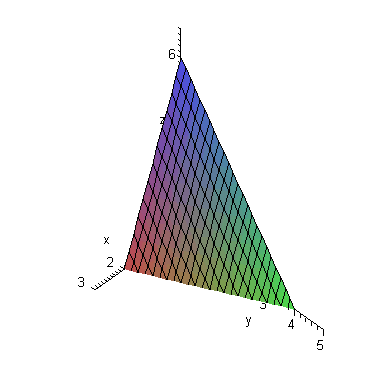
Рисунок. 1.21
Решение
Имеет место формула
. (1.10)
Мы имеем:
и
.
Проекцией данной
плоскости на плоскость xOy
является треугольник, ограниченный
координатными осями Ox,
Oy и прямой
(последняя получается из уравнения
данной плоскости при z
= 0). Получим:
S
=
=
=
=
=
= 14.
Вычисление интеграла в Maple происходит следующим образом:
> with(student):Doubleint(7/2, y=0..4-2*x, x=0..2);
> value(%);
ПРИМЕР 2.
Вычислить площадь части поверхности
,
вырезанной цилиндром
.
Решение
Контуром проекции
вырезанной части на плоскость xOy
является лемниската
(рис.1.22).
Построим общий вид пересекающихся поверхностей.
> with(plots):
> with(student):
> A1:=plot3d([(u),(v),((u^2+v^2)/2)],u=-4..4,v=-4..4,axes=normal):
> A2:=plot3d([(u),((1/2)*sqrt(-2-4*u^2+2*sqrt(8*u^2+1))),(v)],u=-1..1,v=-1..1,axes=normal):
> A3:=plot3d([(u),(-(1/2)*sqrt(-2-4*u^2+2*sqrt(8*u^2+1))),(v)],u=-1..1,v=-1..1,axes=normal):
> display({A1,A2,A3,A4,A5},labels=[x,y,z],scaling=constrained,view = [-1.5 .. 1.5, -1.5 .. 1.5, 0 .. 1]);
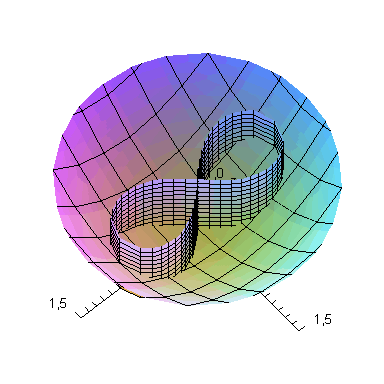
Рис. 1.22
Построим вырезаемую цилиндром поверхность:
>
>
>
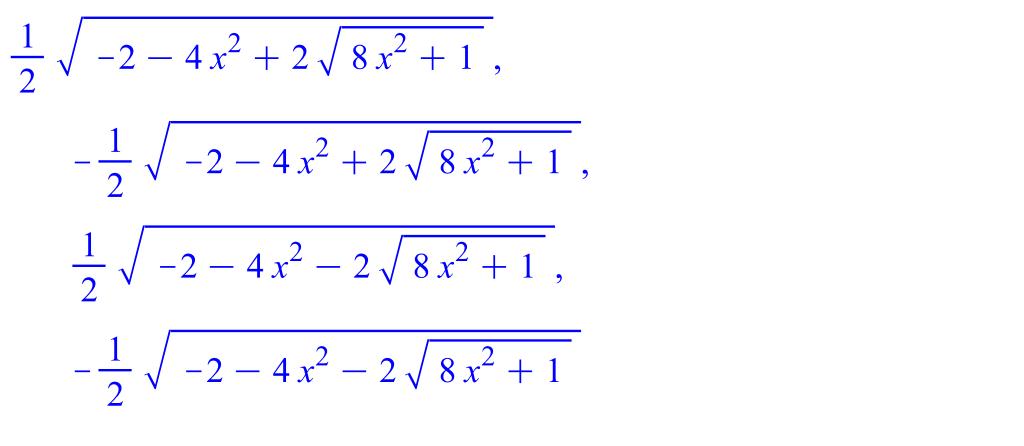
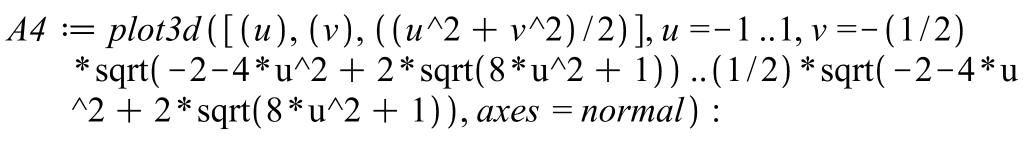
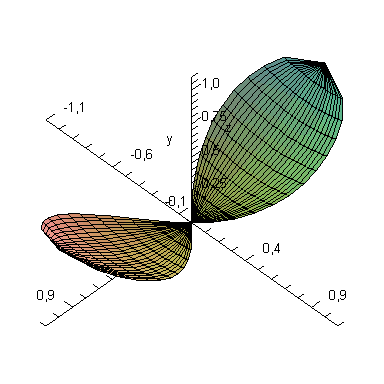
Рисунок. 1.23
Цилиндр вырезает
из параболоида два равных куска
поверхности. Чтобы вычислить их общую
площадь, воспользуемся формулой (1.10).
Для нее из уравнения параболоида
получим подынтегральную функцию.
,
.
Следовательно,
.
Преобразуем интеграл к полярным
координатам
.
Подынтегральная функция запишется в
виде
,
а уравнение лемнискаты – в виде
,
или
.
Так как параболоид
и цилиндр симметричны относительно
плоскостей xOz, yOz,
то достаточно вычислить интеграл по
одной четвертой части лемнискаты,
расположенной в первой четверти плоскости
xOz. Следовательно,
пределами интегрирования будут:
.
Получим:
,
откуда
.
Вычисление интеграла в Maple происходит следующим образом:
> with(student):Doubleint(4*rho*sqrt(1+rho^2), rho=0..sqrt(cos(2*phi)), phi=0..Pi/4);
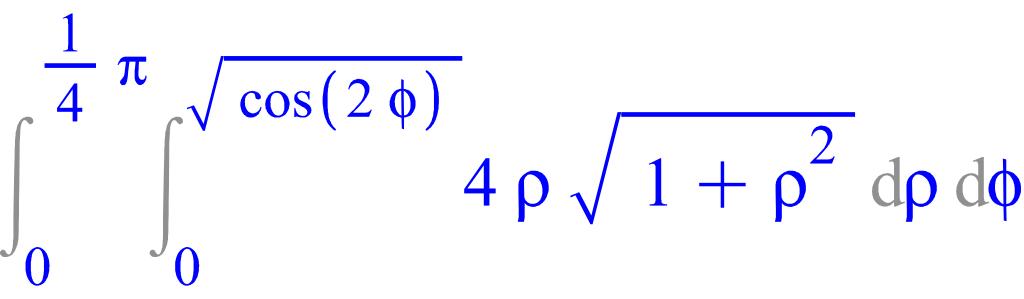
> value(%);
2. Тройные интегралы
2.1. Задача о вычислении массы тела
Рассмотрим тело
(V),
плотность
которого известна, но переменна, т.е. в
разных точках различна, и предположим,
что нам требуется подсчитать массу
этого тела. Для этого разобьем тело (V)
произвольным образом на элементарные
тела
соответственно с объемами
и выберем в каждом из них по точке
.
Примем приближенно, что в пределах
элементарного тела
плотность постоянна и равна плотности
в выбранной точке. Тогда масса
каждого элементарного тела приближенно
выразится следующим образом:
,
масса же всего тела будет
.
В пределе, при стремлении к нулю наибольшего из диаметров d всех областей , это равенство делается точным, так что
,
(2.1)
и задача решена.
Предел этого
вида и есть тройной
интеграл от
функции
по области
при условии, что он не зависит от вида
разбиения и выбора точек Mk.
В принятых нами для них обозначениях
полученный выше результат запишется
так:
.