Решение
Данное тело изображено на рисунке 1.18.
> with(plots):
> with(student):
> A1:=plot3d([(u),(u^2),(v)],u=0..1,v=0..1-u,axes=normal):
> A2:=plot3d([(u),(u),(v)],u=0..1,v=0..1-u,axes=normal):
> A3:=plot3d([(u),(v),(1-u/2-v/2)],u=0..1,v=u^2..u,axes=normal):
> A4:=plot3d([(u),(v),(0)],u=0..1,v=u^2..u,axes=normal):
> display({A1,A2,A3,A4},labels=[x,y,z],scaling=constrained,view = [0 .. 1.5, 0 .. 1.5, 0 .. 1.5]);
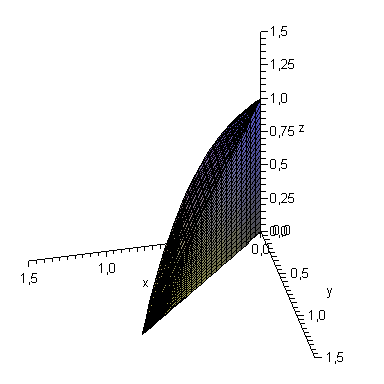
Рисунок. 1.18
Подынтегральная
функция
.
Область интегрирования (D)
ограничена прямой
и параболой
.
При определении пределов интегрирования
пользуемся уже известным приемом.
Получим
и по формуле (1.2*)
V
=
=
=
=
=
=
=
=
.
Вычисление интеграла в Maple происходит следующим образом:
> with(student):Doubleint((1/2)*(2-x-y), y=x^2..x, x=0..1);
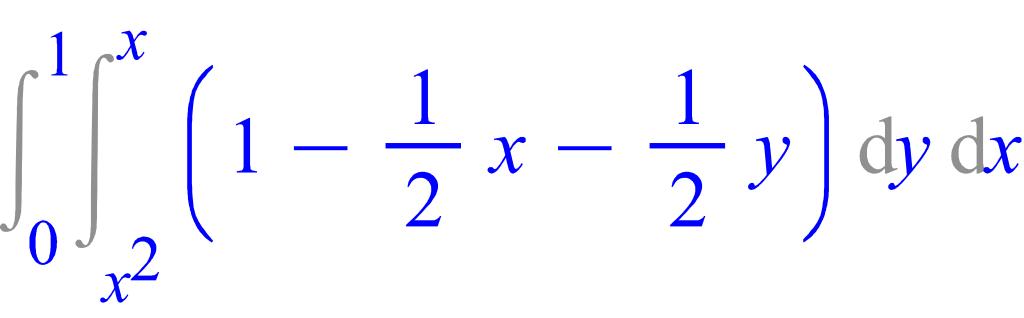
> value(%);
ПРИМЕР 4. Оси двух круговых цилиндров с одинаковыми радиусами поперечных сечений пересекаются под прямым углом. Вычислить объем общей части этих цилиндров.
Решение
Обозначим радиус
поперечного сечения каждого из цилиндров
через r. Выберем
прямоугольную систему координат в
пространстве таким образом, чтобы оси
цилиндров совпадали с осями Oy
и Oz. Тогда уравнения
цилиндрических поверхностей будут
иметь вид:
- цилиндрическая поверхность с осью
симметрии Oy,
- цилиндрическая поверхность с осью
симметрии Oz. На рисунке
(1.19) отмечена одна восьмая часть тела,
получаемого указанным сечением двух
цилиндрических тел.
> with(plots):
> with(student):
> A1:=plot3d([(u),(v),(sqrt(1-u^2))],u=0..1,v=0..sqrt(1-u^2),axes=normal):
> A2:=plot3d([(u),(sqrt(1-u^2)),(v)],u=0..1,v=0..sqrt(1-u^2),axes=normal):
> A3:=plot3d([(0),(u),(v)],u=0..1,v=0..1,axes=normal):
> A4:=plot3d([(u),(v),(0)],u=0..1,v=0..sqrt(1-u^2),axes=normal):
> display({A1,A2,A3,A4},labels=[x,y,z],scaling=constrained,view = [0 .. 1.1, 0 .. 1.1, 0 .. 1.1]);
Рисунок. 1.19
Подынтегральной
функцией будет, очевидно, разрешенное
относительно y уравнение
поверхности цилиндра с осью симметрии
Oy, т.е.
.
Проектируя ее часть, отрезанную второй
поверхностью и содержащуюся в первом
октанте, получим область интегрирования
при вычислении объема выделенной на
рисунке части тела. Ею будет часть круга
,
расположенная в первой четверти плоскости
xOy. Если по x
взять постоянные пределы (
),
то по y будут
пределами: 0 - нижний предел, а
- верхний. Тогда
=
=
= r3 –
=
.
Следовательно,
Вычисление интеграла в Maple происходит следующим образом:
> with(student):Doubleint(8*sqrt(r^2-x^2), y=0..sqrt(r^2-x^2), x=0..r);
> value(%);
ПРИМЕР 5.
Вычислить объем тела, ограниченного
поверхностями
Решение
Поверхность
есть круговой цилиндр, ось которого
параллельна оси Oz, а
и
- плоскости, проходящие через ось Oy
под разными углами наклона к плоскости
xOy. Эти плоскости,
пересекая цилиндр, вырезают из него
клинообразный слой (рис.1.20), объем
которого и требуется вычислить.
> with(plots):
> with(student):
> A1:=plot3d([(u),(sqrt(4*u-u^2)),(v)],u=0..4,v=u..2*u,axes=normal):
> A2:=plot3d([(u),(-sqrt(4*u-u^2)),(v)],u=0..4,v=u..2*u,axes=normal):
> A3:=plot3d([(u),(v),(u)],u=0..4,v=-sqrt(4*u-u^2)..sqrt(4*u-u^2),axes=normal):
> A4:=plot3d([(u),(v),(2*u)],u=0..4,v=-sqrt(4*u-u^2)..sqrt(4*u-u^2),axes=normal):
> display({A1,A2,A3,A4},labels=[x,y,z],scaling=constrained,view = [0 .. 4, -4 .. 4, 0 .. 8]);
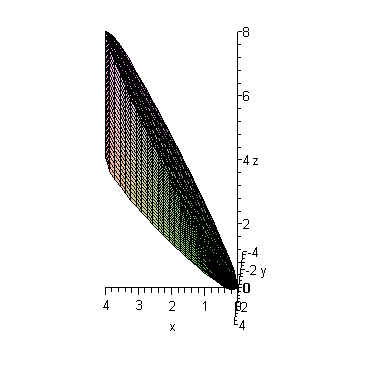
Рисунок. 1.20
Сам слой не является
цилиндрическим брусом, и потому его
объем не может быть вычислен непосредственно
по формуле (1.2*). Однако его можно
рассматривать как разность двух
цилиндрических брусов, срезанных сверху
плоскостями
и
.
Пределы изменения для x
и y находим из уравнения
контура области интегрирования
.
Здесь удобнее взять постоянные пределы
по
.
Тогда по y будут: 0 –
нижний предел,
- верхний предел, и искомая половина
объема тела представится в виде:
Следовательно, V = 8π.
Вычисление интеграла в Maple происходит следующим образом:
> with(student):(Doubleint(2*x, y=0..sqrt(4*x-x^2), x=0..4)-Doubleint(x, y=0..sqrt(4*x-x^2), x=0..4))*2;
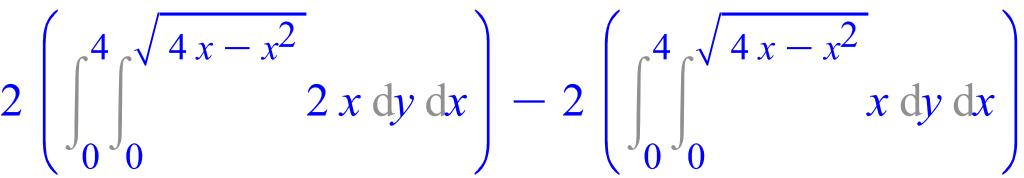
> value(%);
