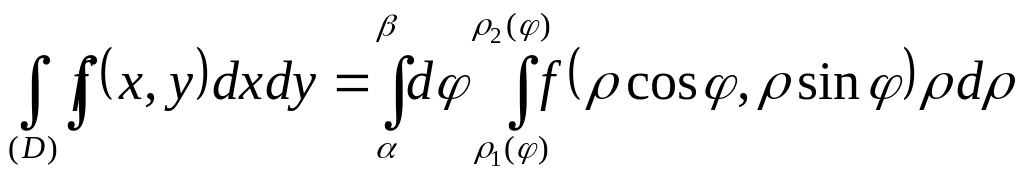1.5.2. Замена переменных в двойных интегралах

Предположим, что даны две декартовы плоскости с осями x,y и u,v. Рассмотрим в этих плоскостях две замкнутые области: область (D) на плоскости и область на плоскости . Каждая из этих областей может быть и неограниченной, в частности может охватывать и всю плоскость. Границу области (если область не охватывает всей плоскости) будем предполагать кусочно-гладкой кривой.

Рисунок.1.13

Допустим, что в области дана система непрерывных функций

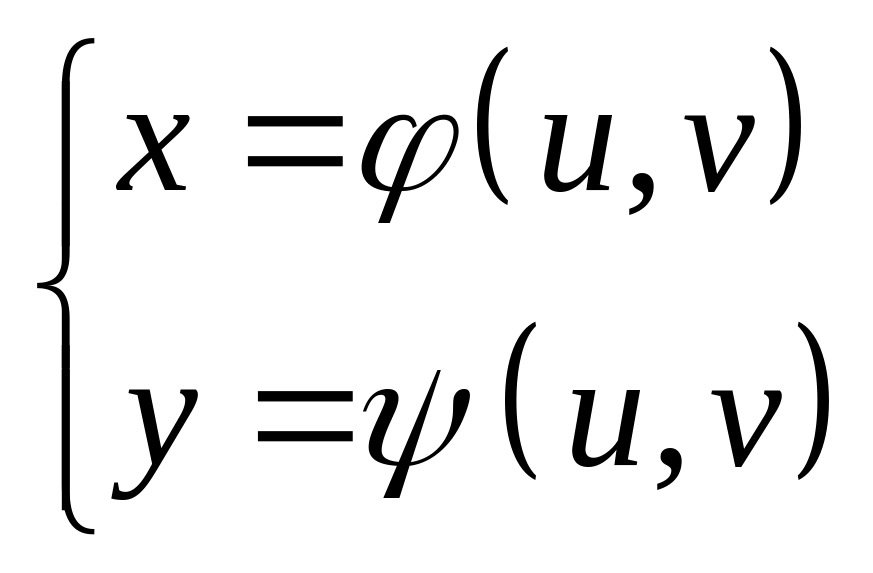_, (1.5)

которая устанавливает между областями (D) и взаимно однозначное соответствие. Задание пары значений переменных u и v из области однозначно определяет некоторую точку в области (D) на плоскости (и обратно). Это дает основание и числа u,v называть координатами точек области (D).

Кривую, составленную из точек области (D), у которых одна из координат сохраняет постоянное значение, называют координатной линией. В связи с тем, что координатные линии, вообще говоря, будут кривыми, числа u,v, характеризующие положение точки на плоскости , и в этом случае (как и в случае кривой поверхности) называют криволинейными координатами точки.

Придавая координате u различные (возможные для нее) постоянные значения, получим семейство координатных линий на плоскости . Фиксируя значение координаты v, получим другое семейство координатных линий. При наличии взаимно однозначного соответствия между рассматриваемыми областями различные линии одного и того же семейства не пересекаются между собой, и через любую точку области (D) проходит по одной линии из каждого семейства.

Вся сетка координатных линий на плоскости является изображением сетки прямых u = const и v = const на плоскости (рис.1.13).

Далее будем предполагать, что функции (1.5) не только непрерывны, но и имеют непрерывные частные производные первого порядка.

Определение 5. Определитель второго порядка следующего вида

(1.6)

называют якобианом перехода от декартовых координат к криволинейным и обозначают .

Тогда формула перехода от декартовых координат к криволинейным координатам имеет следующий вид:

, (1.7)

≠ 0, за исключением конечного числа точек.

ЗАМЕЧАНИЕ 3. На практике декартовые координаты точки и ее криволинейные координаты рассматривают не на разных координатных плоскостях, а на одной совмещенной.

Простейшим и важнейшим примером криволинейных координат являются полярные координаты . Они имеют наглядное геометрическое истолкование, как полярный радиус-вектор и полярный угол, но могут быть введены и формально, с помощью соотношений:

. (1.8)

Если значения и откладывать по двум взаимно перпендикулярным осям, считая, скажем, - абсциссой, а - ординатой (при правой ориентации осей), то каждой точке полуплоскости по указанным формулам отвечает одна определенная точка на плоскости .

Прямым отвечают круги радиуса с центром в начале (полюсе), а прямым отвечают лучи, исходящие из начала (полюса) под углом к оси (рис. 1.14).

Рисунок. 1.14

Однако в данном случае формулы преобразования не будут однозначно разрешимы: изменения величины угла на (где k – целое) не отразится на значениях x и y. Для того чтобы получить все точки плоскости , достаточно ограничиться значениями ρ ≥ 0, 0 ≤ φ < 2π. Каждой точке (x,y), отличной от начала, отвечает одно значение ρ > 0 и одно значение φ в указанных пределах. Но неустранимое нарушение однозначности соответствия связано с началом координат: точке x = y = 0 отвечает на плоскости вся ось (или, если угодно, отрезок ее от до ).

Формулы (1.8) называют формулами связи между декартовыми и полярными координатами.

Используя формулу (1.6), вычисляем якобиан перехода от декартовых координат к полярным:

= = = .

Тогда, используя формулу (1.7), формула перехода от декартовых координат к полярным принимает следующий вид:

. (1.9)

ОПРЕДЕЛЕНИЕ 6. Область (D) называется правильной в направлении полярной оси , если луч, проходящий через внутренние точки области (D), пересекает границу области в двух точках (рис.1.15).

Рисунок. 1.15

Следующая теорема позволяет вычислять двойной интеграл в полярных координатах (см. замечание 3).

ТЕОРЕМА 5. Если функция непрерывна в области , область - правильная в направлении полярной оси (рис. 1.15), то

.

Тогда по формуле (1.9) получаем: