Решение

Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.18).

> with(plots):

> with(student):

> A1:=plot3d([(u),(v),(5*(u^2+v^2)+2)],u=-(1-(v-1)^2)^0.5..(1-(v-1)^2)^0.5,v=0..2,axes=normal):

> A2:=plot3d([(u),(v),(2+10*v)],u=-(1-(v-1)^2)^0.5..(1-(v-1)^2)^0.5,v=0..2,axes=normal):

> display({A1,A2},labels=[x,y,z]);

Рисунок. 2.18

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области V на выбранную плоскость изображена на рис. 2.19.

> A5:=plot3d([(u),(v),(0)],u=-(1-(v-1)^2)^0.5..(1-(v-1)^2)^0.5,v=0..2,color=blue,style=patch,axes=normal):

> display({A5},labels=[x,y,z],scaling=constrained);

Рисунок. 2.19

Так как одна из образующих поверхности тела – параболоид вращения, то удобнее перейти в цилиндрическую систему координат. Уравнения поверхностей в цилиндрической системе координат имеют вид:

z = 5ρ² + 2 – уравнение параболоида вращения,

z = 2 + 10ρsinφ – уравнение плоскости.

Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.18) по переменной z от 5ρ² + 2 до 2 + 10ρsinφ, по переменной ρ от 0 до 2sinφ, по φ от 0 до π (т.к. проекция на плоскость xOy – окружность с единичным радиусом и с центром в точке (0, –1), рис. 2.19). Тогда, с учетом якобиана перехода, имеем:

= = = =

= = =

= = =

= = = = .

Вычислим этот интеграл в Maple.

> with(student):

> Tripleint(rho, z=5*rho^2+2..2+10*rho*sin(phi), rho=0..2*sin(phi), phi=0..Pi);

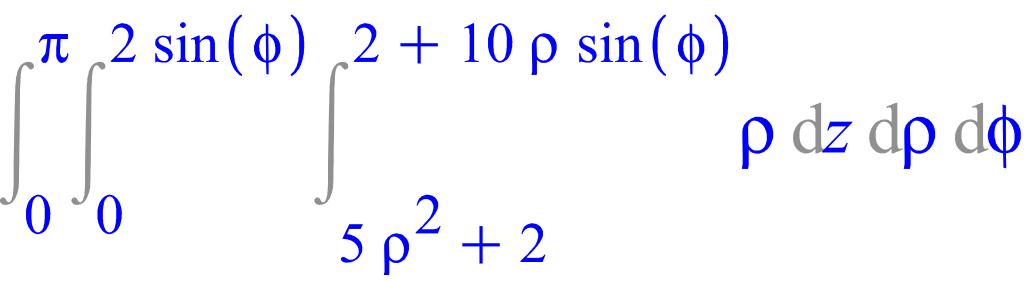
> value(%);

Пример 6. Найти объем тела, заданного неравенствами:

9 ≤ x² + y² + z² ≤ 81, 0 ≤ z ≤ , y ≤ 0, y ≤ – х.

Решение

Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.20).

> with(plots):

> with(student):

> A1:=plot3d([(9*cos(phi)*sin(theta)),(9*sin(phi)*sin(theta)),(9*cos(theta))],phi=-Pi..-Pi/4,theta=arctan(sqrt(80))..Pi/2,axes=boxed):

> A2:=plot3d([(3*cos(phi)*sin(theta)),(3*sin(phi)*sin(theta)),(3*cos(theta))],phi=-Pi..-Pi/4,theta=arctan(sqrt(80))..Pi/2,axes=boxed):

> A3:=plot3d([(p*cos(-Pi)*sin(theta)),(p*sin(-Pi)*sin(theta)),(p*cos(theta))],p=3..9,theta=arctan(sqrt(80))..Pi/2,axes=boxed):

> A4:=plot3d([(p*cos(-Pi/4)*sin(theta)),(p*sin(-Pi/4)*sin(theta)),(p*cos(theta))],p=3..9,theta=arctan(sqrt(80))..Pi/2,axes=boxed):

> A5:=plot3d([(p*cos(phi)*sin(arctan(sqrt(80)))),(p*sin(phi)*sin(arctan(sqrt(80)))),(p*cos(arctan(sqrt(80))))],p=3..9,phi=-Pi..-Pi/4,axes=boxed):

> A6:=plot3d([(p*cos(phi)*sin(Pi/2)),(p*sin(phi)*sin(Pi/2)),(p*cos(Pi/2))],p=3..9,phi=-Pi..-Pi/4,axes=boxed):

> display({A1, A2, A3, A4, A5, A6}, scaling = constrained, axes = normal, labels = [x, y, z], view = [-10 .. 8, -10 .. 4, 0 .. 1]);

Рисунок. 2.20

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области V на выбранную плоскость изображена на рис. 2.21.

Рисунок. 2.21

Рассмотрим первое двойное неравенство 9 ≤ x² + y² + z² ≤ 81. Это пространство, заключенное между двумя сферами с радиусами 3 и 9, расположенными в начале координат.

Так как одна из образующих поверхности тела – сферы, то удобнее перейти в сферическую систему координат. Уравнения поверхностей в сферической системе координат имеют вид:

9 ≤ ρ ≤ 81 – сферы и пространство между ними.

Второе двойное неравенство 0 ≤ z ≤ задает пространство между плоскость z = 0 и конусом z = . Уравнение плоскости z = 0 в сферической системе координат получим исходя из формул связи между прямоугольной декартовой системой координат и сферической:

ρcosΘ = 0,

откуда ρ  R, Θ = (без учета периода).

Уравнение конуса найдем следующим образом. Пусть х = 0, тогда:

z = .

Следовательно = .

Для решения тригонометрического уравнения воспользуемся формулами приведения:

ctg(Θ) = .

Следовательно, tg(Θ) = .

Полученное решение является уравнением конуса в сферической системе координат.

Отсюда, решение, соответствующее условию задачи, имеет вид:

Θ = arctg( ).

Полученное решение является уравнением конуса в сферической системе координат.

Следовательно, второе двойное неравенство, определяющее пространство между плоскостью и конусом, с учетом того, что угол Θ отсчитывается от оси z в направлении по часовой стрелке, имеет вид:

arctg( ) ≤ Θ ≤ .

Третье y ≤ 0 и четвертое неравенства y ≤ – х задают полупространства, ограниченные соответствующими плоскостями y = 0, ниже оси х (отрицательные значения у) и y = – х, ниже соответствующей плоскости, их проекции изображены на рис. 2.21.

Исходя из связи между декартовой и сферической системами координат, учитывая положительное направление отсчета угла φ, эти неравенства можно сразу записать в сферической системе координат:

φ ≥ π, φ ≤ ,

Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.20) по переменной Θ от arctg( ) до , по переменной ρ от 3 до 9, по φ от π до . Тогда, с учетом якобиана перехода, имеем:

= = =

= 234 =

= 26 = 26 = .

ЗАМЕЧАНИЕ. Во время вычисления интеграла возникает необходимость вычислять cos(arctg( )). Оно осуществляется с применением формулы (справедливой только для положительных значений аргумента х):

arctg х = arccos , а cos(arccosx) = x.

Вычислим этот интеграл в Maple.

> with(student):

> Tripleint(rho^2*sin(Theta), rho=3..9, Theta=arctan(sqrt(80))..Pi/2, phi=Pi..7*Pi/4);

> value(%);

Пример 7. Тело V задано ограничивающими его поверхностями, μ – плотность. Найти массу тела.

x² + y² = z², x² + y² = 4, y = 0, z = 0 (y ≥ 0, z ≥ 0); μ = 5(x² + y²).