Решение

Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.14).

> with(plots):

> with(student):

> A1:=plot3d([(u),(-u^2+3),(v)],u=-1..1,v=1-u^2+2*(-u^2+3)^2..5-u^2+2*(-u^2+3)^2,axes=normal):

> A2:=plot3d([(u),(2),(v)],u=-1..1,v=(1-u^2+8)..(5-u^2+8),axes=normal):

> A3:=plot3d([(u),(v),((1-u^2+2*v^2))],u=-1..1,v=2..(-u^2+3),axes=normal):

> A4:=plot3d([(u),(v),(5-u^2+2*v^2)],u=-1..1,v=2..(-u^2+3),axes=normal):

> A5:=plot3d([(u),(v),(0)],u=-1..1,v=2..(-u^2+3),axes=normal):

> display({A1,A2,A3,A4},labels=[x,y,z],view=[-1..1,0..3,0..23]);

Рисунок. 2.14

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области V на выбранную плоскость изображена на рис. 2.15. Построим ее аналогично предыдущей задаче.

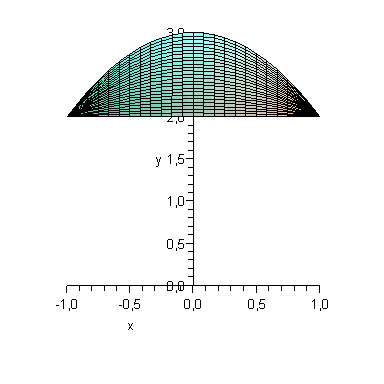
Рисунок. 2.15

Область является правильной относительно всех осей.

Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.15) по переменной y от 2 до –х² + 3, по x от –1 до 1, и, в соответствии с рис. 1 по оси z от гиперболического параболоида z = 1 – x² + 2y² до такого же точно гиперболического параболоида, смещенного по оси z на четыре единицы вверх z = 5 – x² + 2y².

= = = =

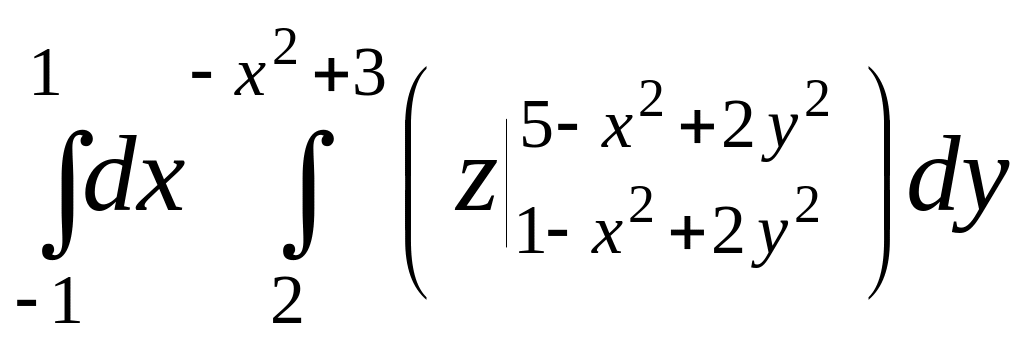4 = 4 = 4· = .

Вычислим этот интеграл в Maple.

> with(student):

> Tripleint(1, z=1-x^2+2*y^2..5-x^2+2*y^2, y=2..-x^2+3, x=-1..1);

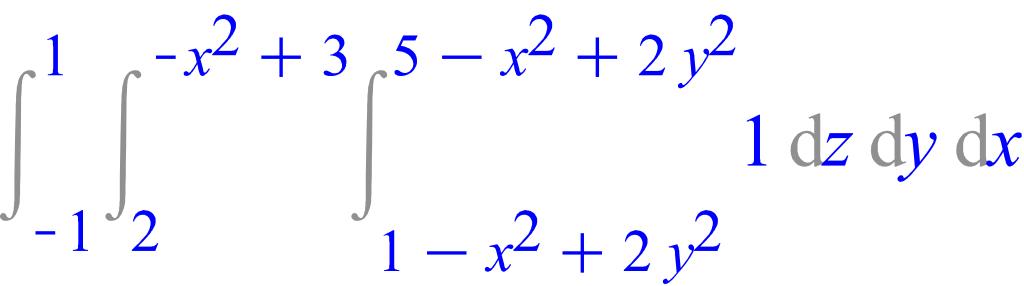
> value(%);

Пример 4. Найти объем тела, заданного ограничивающими его поверхностями: z = , z = (участком сферы и конуса).

Решение

Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.16).

> with(plots):

> with(student):

> A1:=plot3d([(u),(v),((9-u^2-v^2)^0.5)],u=-3*3^0.5/2..3*3^0.5/2,v=-(27/4-u^2)^0.5..(27/4-u^2)^0.5,axes=normal):

> A2:=plot3d([(u),(v),(((u^2+v^2)/3)^0.5)],u=-3*3^0.5/2..3*3^0.5/2,v=-(27/4-u^2)^0.5..(27/4-u^2)^0.5,axes=normal):

> A3:=plot3d([(u),(v),((9-u^2-v^2)^0.5)],u=-(27/4-v^2)^0.5..(27/4-v^2)^0.5,v=-3*3^0.5/2..3*3^0.5/2,axes=normal):

> A4:=plot3d([(u),(v),(((u^2+v^2)/3)^0.5)],u=-(27/4-v^2)^0.5..(27/4-v^2)^0.5,v=-3*3^0.5/2..3*3^0.5/2,axes=normal):

> A5:=plot3d([(u),(v),(0)],u=-(27/4-v^2)^0.5..(27/4-v^2)^0.5,v=-3*3^0.5/2..3*3^0.5/2,color=blue,style=patch,axes=normal):

> A6:=plot3d([(u),(v),(0)],v=-(27/4-u^2)^0.5..(27/4-u^2)^0.5,u=-3*3^0.5*1/2..3*3^0.5*1/2,color=blue,style=patch,axes=normal):

> display({A1,A2,A3,A4},labels=[x,y,z],scaling=constrained);

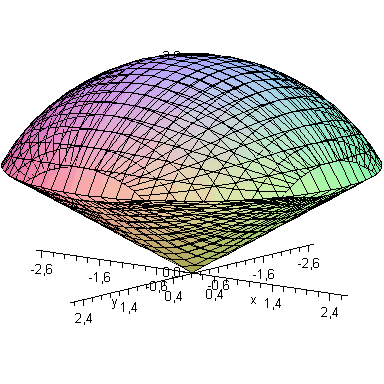
Рисунок. 2.16

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области V на выбранную плоскость изображена на рис. 2.17. Построим ее, используя предыдущее трехмерное построение так:

Рисунок. 2.17

Так как одна из образующих поверхности тела – сфера, то удобнее перейти в сферическую систему координат. Уравнения поверхностей в сферической системе координат имеют вид:

ρ = 3 – уравнение сферы.

Уравнение конуса найдем следующим образом. Пусть х = 0, тогда:

z = , тогда , но ,

после этого, с учетом формулы приведения = .

Решение тригонометрического уравнения, соответствующее условию задачи, имеет вид:

– Θ = или Θ = .

Полученное решение является уравнением конуса в сферической системе координат.

Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.16) по переменной Θ от 0 до , по переменной ρ от 0 до 3, по φ от 0 до 2π (т.к. проекция на плоскость xOy – окружность с центром в начале координат и радиусом рис. 2.17). Тогда, с учетом Якобиана перехода, имеем:

= = =

= = 9 = 9 = 9· ·2π = 9π.

Вычислим этот интеграл в Maple.

> with(student):

> Tripleint(rho^2*sin(Theta), rho=0..3, Theta=0..Pi/3, phi=0..2*Pi);

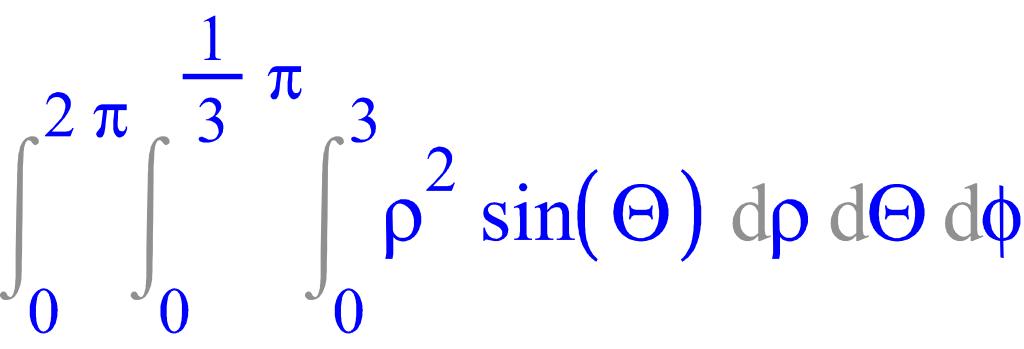
> value(%);

Пример 5. Найти объем тела, заданного ограничивающими его поверхностями: z = 5(x² + y²) + 2, z = 2 + 10y.