2.5. Приложения тройных интегралов
1. Вычисление объема
V
=
.
2. Масса тела
m
=
,
где ρ(x,y,z) – плотность распределения масс в произвольной точке тела (V).
3. Статические моменты
Mxy
=
,
Mzx
=
,
Myz
=
,
Mz
=
.
4. Моменты инерции тела относительно осей координат
Ix
=
,
Iy
=
,
Iz
=
.
5. Координаты центра тяжести тела
Xc
=
,
Yc
=
,
Zc
=
.
Пример 1. Найти объем тела, заданного ограничивающими его поверхностями:
x
= 5
,
x =
,
z = 0, z
+ y =
.
Решение
Воспользуемся следующей формулой для вычисления объема тела:
V = . (2.11)
Таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.
Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.10).
> restart;
> with(plots):
> with(student):
> A1:=plot3d([(5*sqrt(u)),(u),(v)],u=0..1.5,v=0..(3/2)-u,axes=normal):
> A2:=plot3d([(sqrt(3*u)),(u),(v)],u=0..1.5,v=0..(3/2)-u,axes=normal):
> A3:=plot3d([(u),(v),(0)],u=sqrt(3*v)..5*sqrt(v),v=0..1.5,axes=
normal):
> A4:=plot3d([(u),(v),((3/2)-v)],u=sqrt(3*v)..5*sqrt(v),v=0..1.5,axes=normal):
> display({A1,A2,A3,A4},labels=[x,y,z],scaling=constrained);
С разным масштабом по осям рисунок становится более наглядным.
> display({A1,A2,A3,A4},labels=[x,y,z],scaling=constrained);
Рисунок. 2.10
Область является правильной относительно всех осей. Проектируем тело на плоскость xOy.
Функция inequal не строит графики с нелинейными ограничениями. Поэтому построим график проекции следующими способами.
1. С использованием функции plot.
>
2. С помощью готового трехмерного рисунка. Повернем его так, чтобы стала видна только проекция на требуемую координатную плоскость.
Рисунок. 2.11
Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.11) по переменной y от 0 до (так как область не является простой относительно плоскости xOz), по x от до 5 , и, в соответствии с рис. 1 по оси z от плоскости z = 0 до плоскости z = – y.
=
=
=
=
=
=
=
=
=
.
Вычислим этот интеграл в Maple.
> with(student):
> Tripleint(1, z=0..(3/2)-y, x=sqrt(3*y)..5*sqrt(y), y=0..3/2);
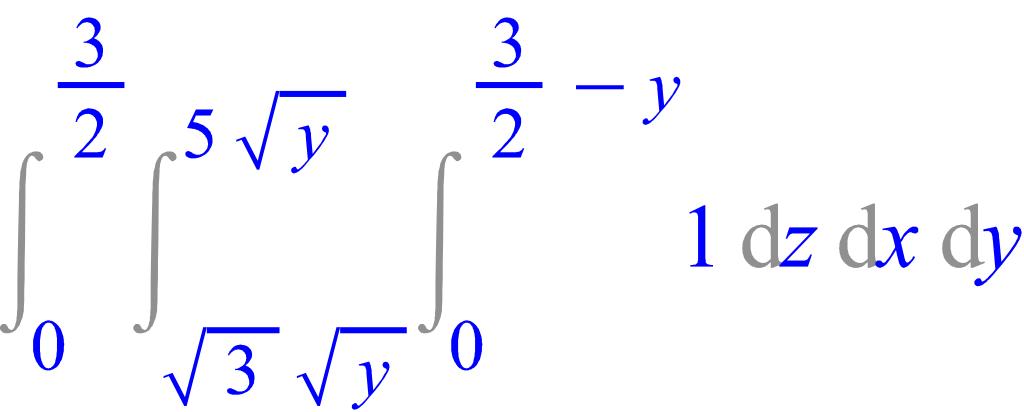
> value(%);
Пример 2. Найти объем тела, заданного ограничивающими его поверхностями: x2 + y2 – 2x = 0, z = 7 – 4y2, z = 1.
Решение
Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.
Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.12).
> with(plots):
> with(student):
> A1:=plot3d([(u),(v),(1)],u=0..2,v=-sqrt(2*u-u^2)..sqrt(2*u-u^2),axes=normal):
> A2:=plot3d([(u),(sqrt(2*u-u^2)),(v)],u=0..2,v=1..7-4*(2*u-u^2),axes=normal):
> A3:=plot3d([(u),(-sqrt(2*u-u^2)),(v)],u=0..2,v=1..7-4*(2*u-u^2),axes=normal):
> A4:=plot3d([(u),(v),(7-4*v^2)],u=0..2,v=-sqrt(2*u-u^2)..sqrt(2*u-u^2),axes=normal):
> A9:=plot3d([x,y,0],x=0..2,y=-(2*x-x^2)^0.5..(2*x-x^2)^0.5,color=red,style=patch):
> display({A1,A2,A3,A4},labels=[x,y,z],scaling=constrained);
Рисунок. 2.12
Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области V на выбранную плоскость изображена на рис. 2.13 и получена разворотом трехмерной фигуры соответствующим образом.
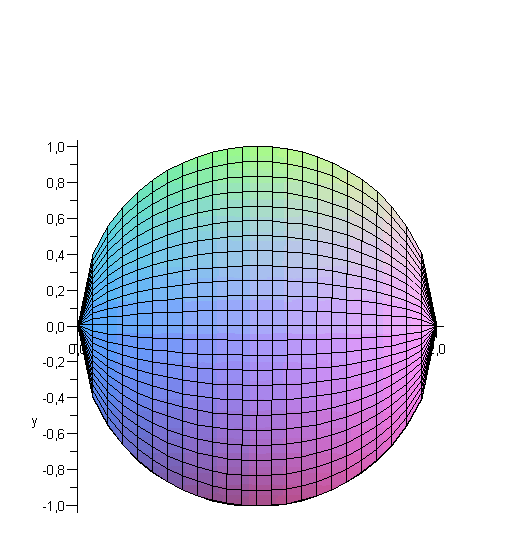
Рисунок. 2.13
Так как одна из образующих поверхности тела – цилиндр, то удобнее перейти в цилиндрическую систему координат. Уравнения поверхностей в цилиндрической системе координат имеют вид:
ρ2 – 2ρcosφ = 0, z = 7 – 4ρ2sin2φ, z = 1.
Тогда исходный
интеграл сводится к повторному, с
пределами интегрирования (рис. 2.12, 2.13)
по переменной z от 1
до 7 – 4ρ2sin2φ,
по переменной ρ от 0 до 2cosφ,
по φ от
до
(т.к. проекция на плоскость xOy
– окружность с единичным радиусом с
центром в точке (1,0) рис. 2.13). Тогда, с
учетом якобиана перехода, имеем:
=
=
=
=
=
=
=
=
=
=
= 5π.
Вычислим этот интеграл в Maple.
> with(student):
> Tripleint(rho, z=1..7-4*rho^2*(sin(phi))^2, rho=0..2*cos(phi), phi=-Pi/2..Pi/2);
> value(%);
Пример 3. Найти объем тела, заданного ограничивающими его поверхностями: y = –x2 + 3, y = 2, z = 1 – x2 + 2y2, z = 5 – x2 + 2y2.