Основная проблема моделирования

Понимание эксперимента зависит от того, какая информация может быть получена из эксперимента с системами.

При постановке и решении задач моделирования пользуются понятием “черного ящика”, введенным У.Р.Эшби. “Черным ящиком” называют систему, внутреннее содержание которой неизвестно наблюдателю, а наблюдению доступны только вход и выход системы.

Выбор этих входов и выходов и есть утверждающая часть модели, которая и будет определять организацию опыта. Конечной целью статистического исследования зависимостей является построение математической модели объекта.

Если осуществить достаточно длительный эксперимент, в котором на вход системы подаются различные входные воздействия и наблюдаются соответствующие им реакции системы, то после анализа результатов эксперимента можно, несмотря на незнание внутренней структуры системы, составить правильное представление о ее поведении. Это дает возможность сделать достаточно достоверное предсказание поведения системы в непроверенных условиях.

Такая процедура была указана еще Леонардо да Винчи (1452 - 1514):

“Нужно руководствоваться показаниями опыта и разнообразить условия до тех пор, пока мы не извлечем из опыта общих законов, ибо лишь опыт открывает нам общие законы”.

Компоненты вектора называют факторами или предикторами(т.е. предсказателями), реакцию системы - откликом. Ограничимся случаем, когда выходной параметр Y – скалярная величина. Неизвестную функцию , которая, как мы предполагаем, связывает и Y, назовем функцией отклика, а ее график – поверхностью отклика.

Итак, описание функционирования черного ящика сводится к установлению соответствия между входами и выходом или, что то же, между факторами и функцией отклика.

Построение модели системы по результатам описанного эксперимента называют идентификацией или структурным синтезом системы.

Пример: моделирование системы с одним входом и одним выходом. Это знакомая задача об интерполяции (или сглаживании) экспериментальной зависимости.

По данным рассмотренного эксперимента (не привлекая дополнительных данных) нельзя сделать общие выводы о внутренней структуре системы, так как одинаковым поведением могут обладать совершенно различные по своей структуре системы. Например, одно и то же соотношение между входами и выходами может согласовываться с несколькими математическими выражениями.

Пусть, например, мы последовательно подаем на вход системы целые числа 1,2,3,4,5,6 и получаем на выходе числа 2,4,6,8,10,12. Разумно предположить, что для любого входного значения n на выходе появляется число 2n и следующими на выходе будут числа 14, 16., 18,..., 2n. Однако результаты опыта столь же хорошо согласуются с формулой

2n+(n-1)(n-2)(n-3)(n-4)(n-5)(n-6).

Основываясь на ней, можно предсказать, что следующими числами в выходной последовательности будут 734, 5056 и т.д. - результат, резко отличающийся от предыдущего.

В любом случае трудность выбора математического выражения, определяющего структуру системы, существенно зависит от априорного знания системы. В зависимости от априорной (доопытной) информации об оригинале различают задачи идентификации в широком и узком смысле. Если природа исследуемого объекта нам неизвестна или известна весьма слабо, то мы имеем дело с идентификацией в широком смысле, т.е. с идентификацией “черного ящика”. Здесь главной является задача обоснования выбора структуры системы. Как отмечалось, сложность решения этой задачи связана с неопределенностью выбора. Если сведения о системе обширны настолько, что можно выбрать типичную математическую схему модели, т.е. задать структуру модели, то остается по результатам опыта оценить лишь неизвестные параметры модели. Здесь мы имеем дело с идентификацией в узком смысле или, иначе, - с идентификацией “серого” ящика. Пример – системы массового обслуживания.

Общая схема моделирования

Сложный объект исследования можно представить так:

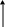
Факторами могут быть, например, характеристики материалов или параметры технологических процессов.

В качестве отклика могут быть, например, физические и химические свойства производимого продукта или технико-экономические показатели процесса. Часто отклик является критерием оптимизации, который требуется максимизировать или минимизировать.

Контролируемые, но не управляемые параметры . В эту группу входят параметры объекта, целенаправленное изменение которых невозможно, например, качество исходного сырья в производстве продукции, которое изменяется от партии к партии.

Неконтролируемые параметры . Это возмущающие воздействия, свойства которых, точки приложения, характер влияния и интенсивность воздействия носят случайный характер (не обязательно статистический) и не поддаются определению. Например, это может быть изменение характеристик оборудования вследствие износа, присутствие случайных примесей, а также случайные ошибки измерения , и .

Мы помним, что задачей эксперимента является поиск математического описания исследуемого объекта – отыскание зависимости между различными группами контролируемых параметров объекта. Наиболее полезно было бы отыскать зависимость такого вида:

.

В случае активного эксперимента (об этом чуть позже) модель объекта ищется в виде

.

Здесь все неуправляемые и неконтролируемые параметры представлены в виде эквивалентного аддитивного шума, отнесенного к выходу объекта:

При этом считается, что случайные компоненты вектора отражают влияние неучтенных на входе факторов.

Заметим, что отклик сложного объекта на одно и то же воздействие зависит от состояния объекта. Исследователь может изменять факторы по своему желанию или хотя бы наблюдать их, контролировать, измерять. Но переменные состояния сложного объекта - это неконтролируемые, ненаблюдаемые переменные, и исследователь может даже не знать об их существовании. Однако их наличие приводит к неоднозначности: на одни и те же внешние воздействия объект дает то одни, то другие реакции; так что одним и тем же значениям факторов могут соответствовать различные значения функции отклика. Примеры: влияние начальных условий в дифференциальных уравнениях и памяти в конечных автоматах.