- •Основная (фундаментальная) задача теории оптимизации и ее 4 части.
- •Основные понятия о системах оптимального управления.
- •Основные типы критериев оптимальности.
- •Классификация оптимальных систем. Определение характеристического критерия, как необходимое условие для применения оптимизационных методов.
- •Определение математической модели технической системы, как необходимое условие для применения оптимизационных методов.
- •Формулировка задачи условной оптимизации с ограничениями.
- •Формулировка задачи безусловной оптимизации.
- •Задачи оценки состояния системы, общие сведения об эстиматорах.
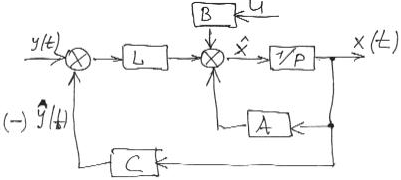
- •Система асимптотической оценки вектора состояния системы, структурная схема.
- •Оптимизация стабилизирующей ос. Интегральный критерий качества и его минимизация.
Оптимизация стабилизирующей ос. Интегральный критерий качества и его минимизация.
Качество стабил. размещ. собств. чисел.
В ранее рассм-ной задаче стабил., когда ОУ описыв. выраж.:
![]()
![]()
И требовалось выбр. ОС
т![]()
![]() ак,
чтобы обесп. уст. замкн. сист.
ак,
чтобы обесп. уст. замкн. сист.
путём размещ. собств. чисел матр. в левой полуплоск. Однако было установлено и большее: собств. числа можно размещ. где угодно и неогранич. увеличивать уст-ть сист.
Т.о. выбор ОС обеспеч. не только уст-ть, но и качество процесса стабилизации, а именно перехода сист. из нач. сост. в окрестность устойчивого полож. равновесия.
Т.е. размещая собств. числа вглубь левой полуплоск. можно обеспечить быстрое достиж. равновесия с люб. точностью. Это связано с ограничениями:
1) тенденция с смещению в левую полупл. собств. чисел замкн. сист. приводит к отклонен. значений некоторых переменных прежде, чем они входят в желаемый допуск => непреемлимое качество стабилизации.
2)обесп. произвол. располож. собств. чисел требует большого уровня упр-щих возд.
В силу 1-го огранич. нельзя считать время практич. затухания процесса приемлемой мерой стабил. сист., с.ч. важно, чтобы в теч. всего процесса отклон. от желаемого сост. были min.
В силу 2-го огранич. важно учесть огранич. на допустимый уровень упр-щих возд.
Оптимизация стабилизирующей ОС. Интегральный критерий качества и его минимизация. Уравнение Риккати.
Теоретически размещая собств. числа матрицы системы А дост. глубоко вглубь левой полуплоскости можно обеспечить сколь угодно быстрое достижение равновесия системы с любой треб. точностью. Однако сущ. 2 ограничения: 1) Тенденция к большому смещению в левую полуплоскость собств. чисел замкн. системы может приводить к большим отклонениям значений некот. переменных прежде, чем они входят в желаемый допуск. Поэтому качество такого процесса стаб-ции нельзя считать приемлимым. 2) Обеспечение произв. расположения собств. чисел м. потребовать очень большого уровня упр. воздействия.
При практической оптимизации оба ограничения формализуют вводя интегральный (энергетический) критерий качества (целевую функцию) процесса стабилизации.
![]()
где qi0 и rk>0 – коэффициенты
![]()
хар-ет «энергию» iй комп. вект.сост.сист.(норму ее отклон. от 0)
![]()
хар-ет энергию кй компоненты вектора управления
Коэф-ты qi задают относительную важность отклонений по каждой координате (некоторые из них м.б. несущественными, тогда qi=0) rk определяют важность «энергетических затрат» по различным управляющим воздействиям. Если оставить в стороне вопрос о том, как в конкретных задачах назначать коэфф-ты соизмерения qi и rk, то можно установить при какой стабилизирующей ОС достигается оптим. значение интегрального критерия кач-ва. Для этого предст. его в матричной форме.
![]()
(**)
Q=diag{q1, q2, … qn}, R=diag{r1, r2, … rk} причем Q – произвольная неотрицательная матр. R – произвольная положительно-определенная матрица. При такой постановке критерия оптимизации, сформулированную выше проблему принято называть задачей оптимальной стабилизации или линейно-квадратичной проблемой оптимального управления. Замечательной особенностью этой задачи явл. то что в ней удается указать вид ОС, дающ. наилучший рез-т при любых нач. услов: Если существует положительно определенная матр. Р, явл. решением матричного квадратичного уравнения след. вида:
ATP + PA - PBR-1BTP + Q=0 (*)
и матр. К связана с Р след. соотн: K=R-1BTP тогда при любых начальн. услов. х0 оптимальн. стабилизация обеспечивается управлением U=-KX причем опт. значение критерия кач-ва будет опред. след. обр.:
Jопт = (X0)T P XT
Ур-е (*) в отечественн. литер. назыв. ур-ем Лурье, а в заруб. – ур-ем Риккати. Для сущ-ния ед. полож. опред. решения Ур-я Рикатти дост-но чтобы пара матриц A и B была невырожденной, R была полож. опр-ной (коэф-ты >0) и было вып-но одно из двух след. условий: 1) Q>0 либо 2) Q0 и предст. в виде Q=CTC и при этом не вырождена пара матриц АТ и СТ
Это положение сводит задачу оптимизации к чисто алгебраической задаче поиска решения матричного уравнения Риккати. Причем если размерность вектора сост. Х равна n то размер искомой матр. Рикатти должен быть nxn поэтому число эл-тов, которые нужно определить при решении – (n(n+1))/2 для определения которых имеем систему ур-й такого же числа.=> решение сложно и без компутера практически неосуществимо.
В реал. сист. не всегда возм. получить инф. о вект. сост. сист., поэтому расм. вариант задачи оптимиз. при отсутств. полной инф. о всех переменных сост. заменив его предпол-м о возм. точн. изм. вых., т.е. вект. откл.Y в люб. момент вр. t≥0. При эт. счит. что вект. сост. X буд. предст. в виде (**)
Тогда мож. быть у-во асимтотич. оц. (эстим.)исп. в к-ве вх. возд. измер. вект. откл. объ. и его вх.U(t) и выраб. оц. вект. сост. как реш. ур. (*)
при
усл. невырожден. матр.![]() ,
матр. L мож. быть выбр. так,
что ошибка вект. сост. буд.→0 при t→∞
при люб. огран. оц. ош. при люб.огран. нач.
ош.
,
матр. L мож. быть выбр. так,
что ошибка вект. сост. буд.→0 при t→∞
при люб. огран. оц. ош. при люб.огран. нач.
ош.![]() ,
,
![]() ,t→∞
для док. дан. выр. необх. из(**) - (*), тогда
,t→∞
для док. дан. выр. необх. из(**) - (*), тогда
![]()
![]() При этом для того чтобы ош. оцен. →0,
след. выбрать матр. L так.,
чтобы матр. A-LC
имела “хорош.”собств.числа, однако они
совп. с собств. числ. AT,LT,CT
при усл. что матр. не вырожд. при эт. стан
очев. что ………………..
При этом для того чтобы ош. оцен. →0,
след. выбрать матр. L так.,
чтобы матр. A-LC
имела “хорош.”собств.числа, однако они
совп. с собств. числ. AT,LT,CT
при усл. что матр. не вырожд. при эт. стан
очев. что ………………..
отлич.
от расм. ранее зад. разм. собств. чис.
матр. A-BK
лишь обозн.![]() и
разреш. с пом. алг. опис. опис. ранее для
невыражд. матр.ATиCT
A→AT
,B→L T
,K→CT
в случ. если AT
и CT
выраждены, но ненаблюд. сист. устойч.
расм. выше выкл. о возм. постр. у-ва справ.
асимтот. оц. остаются в силе однако
говор. о том, что сист. обнаруж-ая или
детектир-ая .Для реальн. сист. при постр.
эстимат. исп. те же матр., что и в опис.
сист. A,B,C
и ввод. те же сам. возд.U(t)поэт.
если нач. усл. вект. сост.X0и
и
разреш. с пом. алг. опис. опис. ранее для
невыражд. матр.ATиCT
A→AT
,B→L T
,K→CT
в случ. если AT
и CT
выраждены, но ненаблюд. сист. устойч.
расм. выше выкл. о возм. постр. у-ва справ.
асимтот. оц. остаются в силе однако
говор. о том, что сист. обнаруж-ая или
детектир-ая .Для реальн. сист. при постр.
эстимат. исп. те же матр., что и в опис.
сист. A,B,C
и ввод. те же сам. возд.U(t)поэт.
если нач. усл. вект. сост.X0и![]() -оц.
совп.то, совп. и дальн. траектор.
-оц.
совп.то, совп. и дальн. траектор.![]() ,t>0.
В эт. случ. сист. асимтотич. оц. раб. также
как и модель сист. Главн. достоин. эстимат.
в том, что она позвол. оц. изм. сост. объ.
и тогда когда нач. знач. неизв. имен. для
эт. цели служ. посл. сост. ввод. в сист.
асимтотич. оц. сигн. обр. связ. пропорц.
разн. между вых.
,t>0.
В эт. случ. сист. асимтотич. оц. раб. также
как и модель сист. Главн. достоин. эстимат.
в том, что она позвол. оц. изм. сост. объ.
и тогда когда нач. знач. неизв. имен. для
эт. цели служ. посл. сост. ввод. в сист.
асимтотич. оц. сигн. обр. связ. пропорц.
разн. между вых.
![]() ,т
е
,т
е
![]() Причем
посл. соотн. будет определять структуру
реализуемую с пом. станд. динамич. звеньев
устр-ва, называемого эстиматором.
Причем
посл. соотн. будет определять структуру
реализуемую с пом. станд. динамич. звеньев
устр-ва, называемого эстиматором.