9. Система асимптотической оценки вектора состояния системы, структурная схема.

В реал. сист. не всегда возм. получить инф. о вект. сост. сист., поэтому расм. вариант задачи оптимиз. при отсутств. полной инф. о всех переменных сост. заменив его предпол-м о возм. точн. изм. вых., т.е. вект. откл.Y в люб. момент вр. t≥0. При эт. счит. что вект. сост. X буд. предст. в виде (**)

Тогда может быть построено устройство асимтотич. оц. (эстиматор), где вх. возд. – это измеряемый вект. отклика объекта и его вх.U(t) и выраб. оц. вект. сост. как реш. ур.

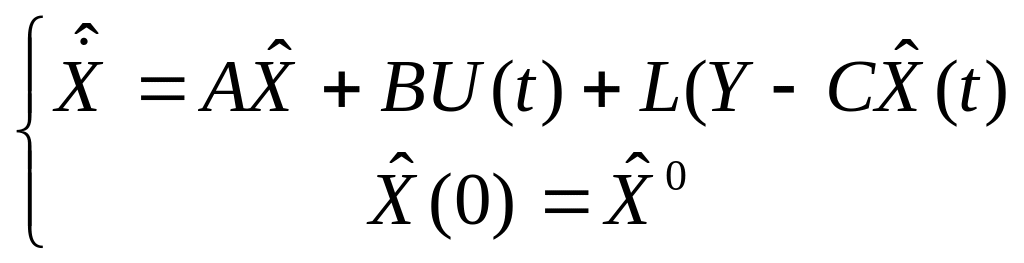
В реал. с-ах не всегда возможно получение новой инф-и о в-ре сост-я с-ы, рассмотрим более сложный вариант построения инженерной оптимизации с-ы при отсутствии полной инф-и о в-ре сост-я с-ы, заменив его предположением о возмож-ти относит-но точного измерения в-ра отклика с-ы Y(t) = CX(t) в любой момент времени t ≥ 0. Будем считать, что в-р сост-я с-ы X(t) опр-ся как пеш-е ур-ий (**)

Тогда м.б. построено устр-во, называемое с-ой асимптотической оценки или эстиматором, исп-щим в кач-ве вх. воздействий измеряемый в-р отклика объекта Y=CX(t) и его вход U(t), и вырабатывающее оценку в-ра сост-я с-ы как реш-е ур-я след. вида: (*)

, причемпри усл-и невырожденности матр-цы с-ы А^Т, С^Т

rank| С^Т | А^ТС^Т | (А^Т)², С^Т…| = n (условие наблюдаемости по Калману) в выраж-и (*) матр. L м.б. выбрана так, что ошибка оценивания в-ра сост-я

, ( - коорд. в-ра сост-я)

будет стремиться к нулю, если t → ∞ при любой ограниченной начальной ошибке в-ра сост-я. Д/док-ва этого высказывания необх. вычесть ур-е (*) из ур-я (**), тогда получим ур-е, определяющее изменение ошибки оценивания т.о.: из этого выраж-я следует, чтобы ошибка → 0, достаточно выбрать матр. L так, чтобы матр. (A – LC) имела «хорошие» (оптим.) собств. числа, однако они совпадают с собств. числами транспонированной матр. (А^T – L^T C^T), если вып-ся усл-е наблюдаемости, т.е матрицы А^Т, С^Т, А, С не особенные, то задача выбора матр. L или L^T отлич-ся от рассмотреннойзадачи размещения собств чисел матр. (А – В К) лишь обозначением, а именно, заменой матр. А на А^Т, К на L^T, В на C^T и разрешима с пом. алг-ов ужеописанных ранее д/невырожд. Пары матриц А^Т, C^T.

Если пара матриц А^Т и C^T вырождена, т.е.усл-е наблюдаемости не вып-ся, но ненаблюдаемая с-а устойчива, представленные выше ф-лы о возм-ти построения д/этой с-ы устр-ва асимптотической оценки остаются в силе, при этом говорят, что такая с-а будет явл-ся обнаруживаемой (детектируемой).

Д/реал. с-м при построении с-ы оценки исп-ют те же матр. А, В, С, что и в описании оптимизируемой с-ы и вводят то же самое внешнее воздействие U(t). Поэтому, если нач. условия в-ра сост-ий с-ы Х(0) = Х⁰ и нач. условия оценки в-ра сост-ий с-ы совпадают, то вовпадают и дальнейшие траектории в-ра сост. и оценки в-ра сост. при всех t > 0. Т.е. с-а оценки объекта работает как модель этого объекта, при этом главное достоинство с-ы оценки б. заключ-ся в том, что она позвол. оценивать изменение сост-я объекта и тогда, когда его начальное сост-е неизв. Именно д/этой цели служит последнее слагаемое в выражении (*), вводящее в с-у оценки сигнал ОС, пропорциональный разности м/д истинным непосредственно измеренным выходом с-ы Y(t) и его прогнозом т.е.:

(*)

опр-ет стр-ру строгореализуемого с пом. стандартных типовых блоков (интеграторы и усилители) устр-ва асимптотич. оценки (эстиматора). Схема эстиматора:

Проблемы размещения собственных чисел, алгоритм решения задачи оптимизация технических систем (при m = 1)

Если мат. м-ль ОУ задана в норм. форме в терминах пр-ва состояния,

где A(n×n), B(n×m)

то требуется найти матрицу K(1×n)

, где (n×n)

имеющую собств. набор чисел λ, удовлетворяющий треб-ям опт-ии. Для этого необх. и дост., чтобы: rank[B₁|AB|…|A^n-1B]=n.

Рассмотрим, когда m=1 (1 вход):

Тогда: 1) должны быть исх. данные: A(n×n), B(n×1), a_k (k=0,1,…,n-1),

(v=1,2,…,n), (n×n). Определить матрицу K(1×n).

Тогда алгоритм нахождения K следующий:

1) вычислить a_k , соответствующие м-це , расположив по степеням λ по формуле:

2) вычислить величины коэффициентов K по формуле:

и составить из них матрицу-строку:

3) построить матрицу преобразования S по формулам:

S_n=B

S_n-1=A·S _n+a_n-1·B=A·B+ a_n-1·B

…….

S₁=A·S₂+a₁·B=A^n-1·B+a_n· +…+a₁·B

где a_n-1 до а₁ – коэф-ты характеристич. полинома этой матрицы.

4) вычислить матрицу К, решив:

Тогда можно получить исх. м-цу, соответствующую оптим. треб-ям.