6. Формулировка задачи условной оптимизации с ограничениями.

Задача общего вида: Минимизировать f(x) при ограничениях h_k(x)=0, где k=1,2,…,k; g_j(x)>=0 j=1,2,…,j ;

функция f(x) называется целевой функцией, уравнение вида h_k(x)=0 называется ограничением в виде равенств, - ограничения сверху и снизу, а g(x)>=0 ограничением в виде неравенств.

Задача, в которой присутствуют ограничения j, k,

называется оптимизационной задачей с ограничениями или задачей условной оптимизации с ограничениями.

Классификация:

1)Если ограничения заданы линейными функциями, то независимо от вида целевой функции, задача называется оптимизационной задачей с линейными ограничениями.

2)Если задача содержит линейную целевую функцию, то она будет задачей линейного программирования.

3)Задачи, в котор. компоненты вектора X принимают только целые значения, называется задачей целочисленного программирования.

4)Задача с нелинейной целевой функцией f(x) и линейными ограничениями называется задачей нелин. программирования с линейными ограничениями.

5)f(x) – квадратичная -> задача квадратичного программирования.

6)f(x) задана отношением линейных функций -> задача дробно-линейного программирования.

Формулировка задачи условной оптимизации с ограничениями.

f(x) – цел.ф-ция (Крит. опт-ции)

h_k(x)=0 – ограничения в виде неравенств

g_j(x) – ограничения в виде неравенств.

Предполагается что все ф-ции вещественные, а число ограничений конечно.

Задача с ограничениями (усл. опт-ции):

Минимиз-ть ф-цию f(x) при ограничениях:

7. Формулировка задачи безусловной оптимизации.

Все задачи оптимизации м. классифицировать, как задачи min некой веществ-ой целевой ф-ии f(x) некоего N-мерного вектора-аргумента X=(x₁,x₂..x_n) компоненты которого удовлетворяют системе уравнений h_k(x)=0 и набору нерав-тв q_i(x)≤0 , а также ограниченное сверху и снизу X_j^в≥X_j≥X_j^н.

h_k(x)=0 – ограничение в виде равенств; q_i(x)≤0 – огр. в виде неравенств.

Задачи в которых ограничения отсутствуют j=k=0 и X_j^в= -X_j^н= ∞ при

j=1,2...N – называются оптимизац-ми задачами без ограничений или задачами безусловной оптимизации.

Формулировка задачи безусловной оптимизации.

f(x) – цел.ф-ция (Крит. опт-ции)

h_k(x)=0 – ограничения в виде неравенств

g_j(x) – ограничения в виде неравенств.

Задача без ограничений (безусл. опт-ции): минимиз-ть ф-цию f(x) при отсутсвии ограничений, если k=j=0 и , где i=1,2,…N.

8. Задачи оценки состояния системы, общие сведения об эстиматорах.

Известная с-а рассматр-ся с учетом случайных вх. воздействий (шумов) W(t) и шумов измерения V(t) так, что измеренный вых. cигнал Z(t) предст. собой искаженное сост-е с-ы, при этом задача предст-ся след. образом (рис.)

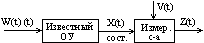
В этом сл. д.б. известны з-ны распредел-я шума с-ы или устр-ва W(t) и шума измерений V(t). При этом треб-ся найти «наилучшую» или оптимальную оценку в-ра сост-я с-ы истинного сост-я с-ы X(t) по известному знач-ю наблюдаемого сост-я с-ы Z(t).

В реал. с-ах не всегда возможно получение новой инф-и о в-ре сост-я с-ы, рассмотрим более сложный вариант построения инженерной оптимизации с-ы при отсутствии полной инф-и о в-ре сост-я с-ы, заменив его предположением о возмож-ти относит-но точного измерения в-ра отклика с-ы Y(t) = CX(t) в любой момент времени t ≥ 0. Будем считать, что в-р сост-я с-ы X(t) опр-ся как пеш-е ур-ий (**)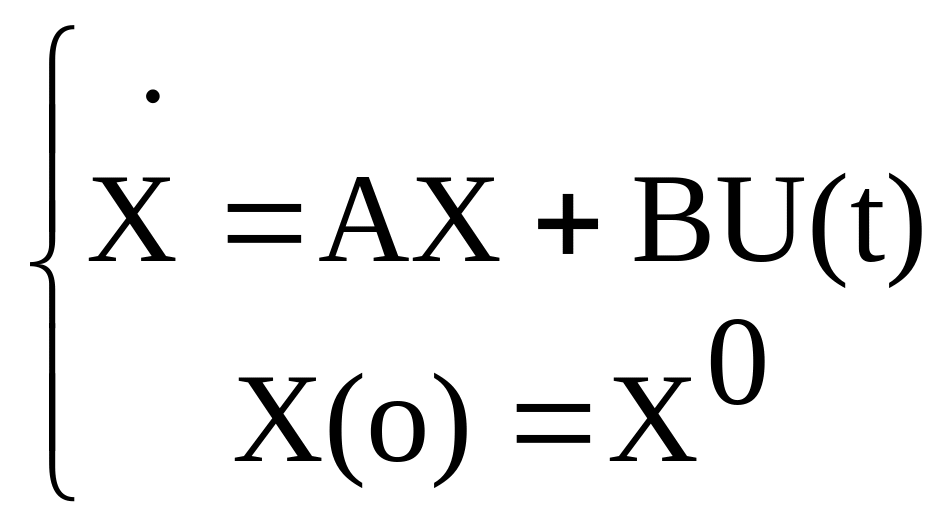

Тогда м.б. построено устр-во, называемое с-ой асимптотической оценки или эстиматором, исп-щим в кач-ве вх. воздействий измеряемый в-р отклика объекта Y=CX(t) и его вход U(t), и вырабатывающее оценку в-ра сост-я с-ы как реш-е ур-я след. вида: (*)

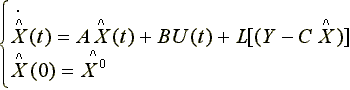, причемпри усл-и невырожденности матр-цы с-ы А^Т, С^Т

rank| С^Т | А^ТС^Т | (А^Т)², С^Т…| = n (условие наблюдаемости по Калману) в выраж-и (*) матр. L м.б. выбрана так, что ошибка оценивания в-ра сост-я

, ( - коорд. в-ра сост-я)

будет стремиться к нулю, если t → ∞ при любой ограниченной начальной ошибке в-ра сост-я. Д/док-ва этого высказывания необх. вычесть ур-е (*) из ур-я (**), тогда получим ур-е, определяющее изменение ошибки оценивания т.о.: из этого выраж-я следует, чтобы ошибка → 0, достаточно выбрать матр. L так, чтобы матр. (A – LC) имела «хорошие» (оптим.) собств. числа, однако они совпадают с собств. числами транспонированной матр. (А^T – L^T C^T), если вып-ся усл-е наблюдаемости, т.е матрицы А^Т, С^Т, А, С не особенные, то задача выбора матр. L или L^T отлич-ся от рассмотреннойзадачи размещения собств чисел матр. (А – В К) лишь обозначением, а именно, заменой матр. А на А^Т, К на L^T, В на C^T и разрешима с пом. алг-ов ужеописанных ранее д/невырожд. Пары матриц А^Т, C^T.

Если пара матриц А^Т и C^T вырождена, т.е.усл-е наблюдаемости не вып-ся, но ненаблюдаемая с-а устойчива, представленные выше ф-лы о возм-ти построения д/этой с-ы устр-ва асимптотической оценки остаются в силе, при этом говорят, что такая с-а будет явл-ся обнаруживаемой (детектируемой).

Д/реал. с-м при построении с-ы оценки исп-ют те же матр. А, В, С, что и в описании оптимизируемой с-ы и вводят то же самое внешнее воздействие U(t). Поэтому, если нач. условия в-ра сост-ий с-ы Х(0) = Х⁰ и нач. условия оценки в-ра сост-ий с-ы совпадают, то вовпадают и дальнейшие траектории в-ра сост. и оценки в-ра сост. при всех t > 0. Т.е. с-а оценки объекта работает как модель этого объекта, при этом главное достоинство с-ы оценки б. заключ-ся в том, что она позвол. оценивать изменение сост-я объекта и тогда, когда его начальное сост-е неизв. Именно д/этой цели служит последнее слагаемое в выражении (*), вводящее в с-у оценки сигнал ОС, пропорциональный разности м/д истинным непосредственно измеренным выходом с-ы Y(t) и его прогнозом т.е.:

(*)

опр-ет стр-ру строгореализуемого с пом. стандартных типовых блоков (интеграторы и усилители) устр-ва асимптотич. оценки (эстиматора). Схема эстиматора:

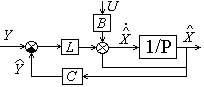
Если мат. м-ль ОУ задана в норм. форме в терминах пр-ва состояния:

где A(n×n), B(n×m)

то требуется найти матрицу K(1×n)

, где (n×n)

имеющую собств. набор чисел λ, удовлетворяющий треб-ям опт-ии. Для этого необх. и дост., чтобы: rank[B₁|AB|…|A^n-1B]=n.

Проблема стабилизации: если пара матриц А и В невырождены и при t=>0 доступен для измер. вектор x(t), тогда с целью оптимальной стабилизации м.б. постр. ОС: U= - KX. Такая сист. устойчива. К м.б. выбрана так, чтобы все числа оказ. в лев. полуплоскости и обладали заданными св-ми:

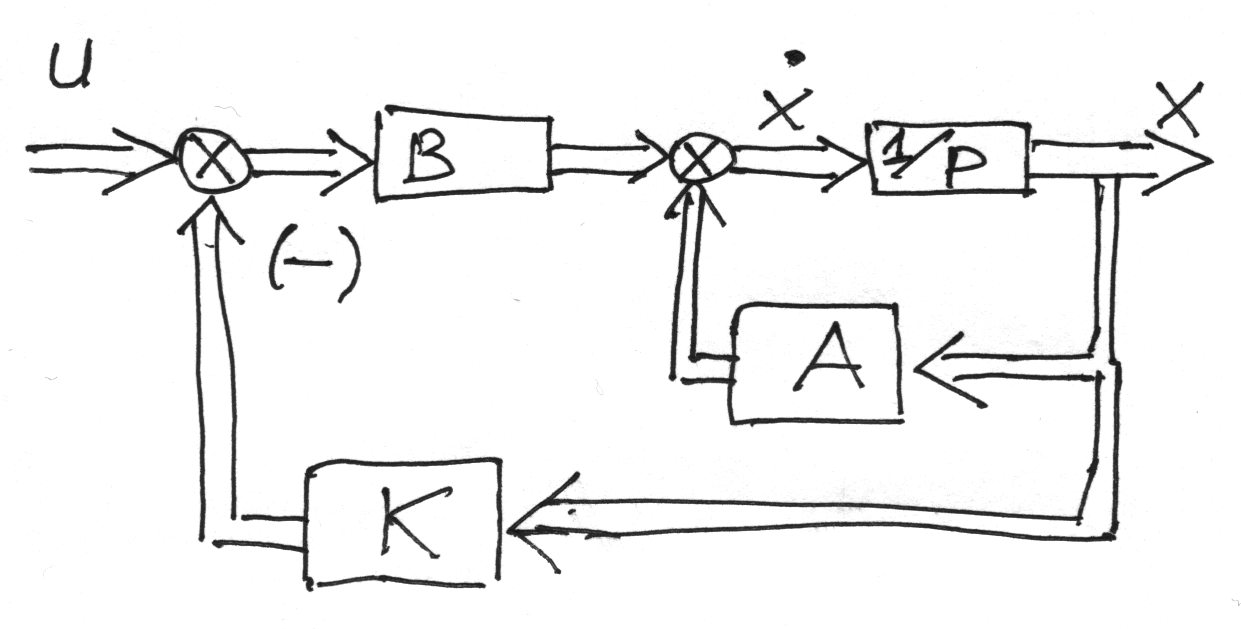
При оптимизации САУ рассматривают 2 варианта (по возможности получения информации о векторе её состояния (полной или неполной).

1-ый вариант проще чем 2-ой, но встречается реже, т.к. применим в основном для простых систем. Если есть математическое описание системы и известно характеристическое уравнение системы (матрица), его корни (собств. числа матрицы системы), то по виду корней можно судить о свойствах системы и, в частности, о её устойчивости.

При оптимизации системы (оптимальная стабилизация), имея возможность влияния на размещение корней в нужной нам области, можно получить такую систему, которая обладала бы желаемыми свойствами.

Методы этой задачи различны, но суть оптимизации системы в изменении свойств системы.