мой курсач

МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ

РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И АВТОМАТИКИ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Факультет: ВАВТ

Кафедра МОВС

Курсовая работа

По дисциплине « ИНФОРМАТИКА»

НА ТЕМУ: « ФОРМИРОВАНИЕ ИНФОРМАЦИИ В ТЕХНИЧЕСКИХ КИБЕРНЕТИЧЕСКИХ СИСТЕМАХ (АЛГОРИТМЫ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ)»

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

ЗАДАНИЕ: ВАРИАНТ №36; N=64; λ=4; j={1,3,4,6}

Начало работы:

Окончание работы:

Руководитель Ильюшенков Э.Ф.

Исполнитель

МОСКВА 2006 г.

1) Задание диапазона измерения реального параметра ОУ - [0, X_max].Пусть X_max = 64 секунды время за которое пловец переплывает через реку. Тогда [0, 64] - диапазон изменения реального параметра (в данном случае времени) ОУ - пловец.

2) Задание аналога (подобия) диапазона [0, X_max] в виде отрезка прямой длины L_max в мм, т.е. [0,L_max]. X_max=L_max =64мм. Отрезок прямой: [0,64] мм

3) Для заданных L_max и количества уровней квантования N определяем разрядность n двоичного кодового эквивалента значения измеряемого параметра L_ и точность дискретного представления ∆x исходя из того, что:

n=log₂64=6 ∆x =64/64=1

4) Для данных n и L_max определяем множество разновесов эталонов , той же природы, что и L_ (в мм), пропорционально соответствующим весам разрядов при двоичном представлении чисел, такое что:  - множество разновесов эталонов (т.е. набора констант для измерения):

e₁=64/2¹=32 при j=1

e₂=64/2²=16 при j=2

e₃=64/2³=8 при j=3

e₄=64/2⁴=4 при j=4

e₅=64/2⁵=2 при j=5

e₆=64/2⁶=1 при j=6

₌ {e₁,e₂, e₃,e₄,e₅,e₆}

5) Множество  представим графически на рис.№1

6) Каждому весу e_j множества  поставим в соответствие класс эталонов Е_j ^{некоторого семейства классов Е такого что , так как n=6 то}

При этом всякий E_j содержит такое количество Q_j эталонов, сумма весов которых равна X_max - e_j т.е.

7) Графическое представление классов эталонов E см. рис №2

8) В соответствии c индивидуальным вариантом задания в системе классов E выделяем  классов эталонов вида Е_j (отмечаем символом * при заданном индексе j) и тем самым задаем конкретный алгоритм из класса алгоритмов: 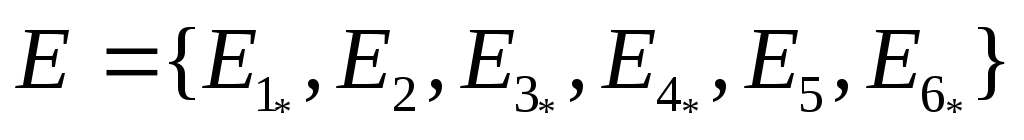. ^{Последовательность из  цифр из} индивидуального варианта задания совпадает c номерами j выделенных для использования в последующем измерении  классов эталонов Е_j  E

 = 4 ( - количество классов эталонов вида Е_j (Е_j  E)).

Выделение осуществляем в составе графического представления системы классов E см. рисунок №2.

9) С целью упорядочивания и облегчения дальнейших построений алгоритма ^{измерения введем сквозную нумерацию заданных классов, заменив} звездочки * на индексы f (1 ≤ f ≤ при индексе j в порядке возрастания j), и ^{заменив на} . ^{В результате получим}

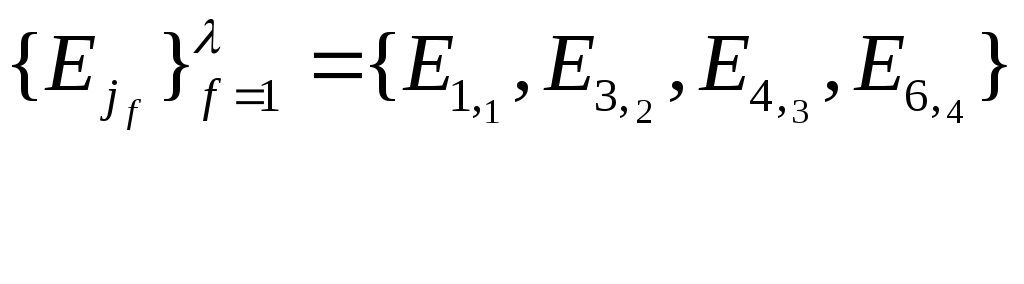
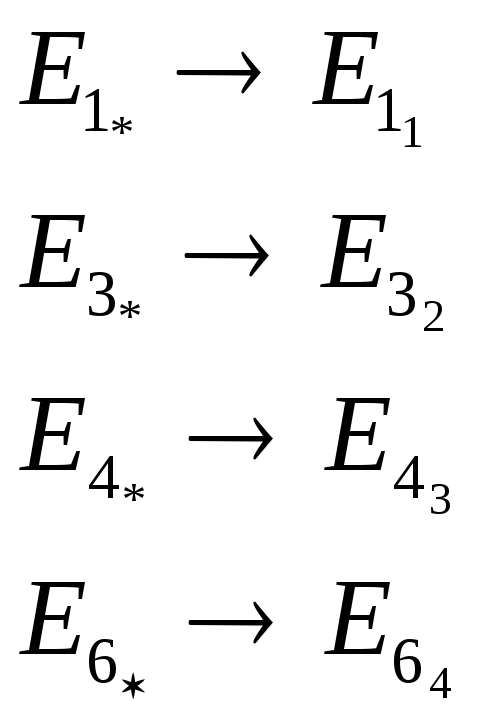^{(при  =4, j={1,3,4,6})}

^{10) Определяем для всех множества (выделенных для} проведения измерения по данному алгоритму, из класса алгоритмов) их частей ^{, так что}  ^{, которые будут непосредственно участвовать в} уравновешивании L_. При этом

q_f - количество частей класса алгоритмов, выделенных для проведения измерения по данному алгоритму, то есть необходимое количество эталонов

разность равная числу двоичных разрядов кода.

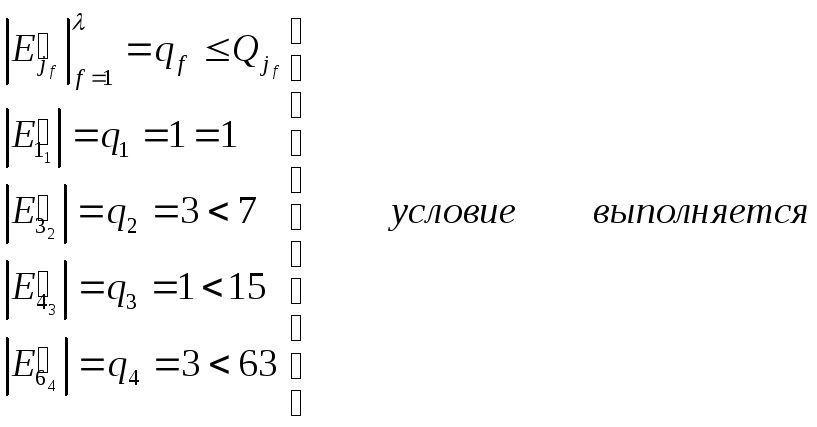
при f =1 m₁=j₁ - j_1-1 = 1-0 = 1 q₁ = 2¹ – 1 = 1

при f =2 m₂=j₂ - j_2-1 = 3-1 = 2 q₂ = 2² – 1 = 3

при f =3 m₃=j₃ - j_3-1 = 4-3 = 1 q₃ = 2¹ – 1 = 1

при f =4 m₄=j₄ - j_4-1 = 6-4 = 2 q₄ = 2² – 1 = 3

где f ={1,2,3,4}

n = 1 + 2 + 1 + 2= 6, где n - разрядность двоичного кодового эквивалента значения, измеряемого параметра L_.

Проверяем выполнение условия:

11) Задание L_ в диапазоне [ 0, L_max], L_ = 34мм 34мм  [0,64]

12) Осуществляем графически последовательную процедуру измерения (ступенчатого уравновешивания) заданного L_ в соответствии c индивидуальным алгоритмом класса алгоритмов ПУ с указанием промежуточных S_f и окончательного S_ результатов первичного измерения. См. рис.№3

13) Графическое уравновешивание заданного L_ сопровождаем последовательной алгоритмической процедурой, состоящей из =4 циклов измерения, последовательной подстановкой в каждый пункт алгоритма для каждого цикла измерения f (от 1 до =4) всех номеров тактов i (от 1 до i_f) формированием для данных f и i.и указанием:

^{I) Всех значений суммы эталонов, используемых для уравновешивания} L_ с выделением S_f

II) Всех значений от результатов проверки логических условий

где P_2,f,i :

P_2,f,i ≡ i < q_f 2 номер условия

P_3,f ≡ f <  f номер цикла

i номер такта

Обозначение оператором каждого из пунктов предписания даётся в конце пункта в круглых скобках.

Начало. Переходим к п. 1 (А)

1. Положить f :=1. Перейти к п.2 (O(f))

2. Положить i_f :=1. Перейти к п.3 (O(i))

3. Из заданного подмножества E′ семейства E выделяем для

^{измерения в текущем цикле f =1 класс эталонов . Перейти к п.4 (E)}

^{4. Из выделенного класса в текущем такте i}_f ^{=1 извлекаем эталон}= e_1,1 для образования составного эталона и последующего уравновешивания выборки L_. Перейти к п.5 (Э)

^{5. Образуем составной эталон цикла f =1 такта i}_f ⁼¹

^S_f,i^=0+1*32=32

где - S_f-1 - сумма весов эталонов или вес составного эталонов или вес составного эталона используемых в уравновешивании L_ цикла f-1 c ^{точностью до S}₀ ^{= 0. Перейти к п.6 (S)}

^{6. Проверяем условие если условие выполняется} переходим к п.7, если нет – к.п.9

P_1,1,1 ≡ 34 > 32 так как условие выполняется переходим к п.7 (P₁)

7. Проверяем условие P_2,f,i ≡ i_f < q_f если условие выполняется переходим к п.8, если нет – к.п.11.

P_2,1,1 ≡ 1 < 1 так как условие не выполняется переходим к п.11 (P₂)

^{11. Произвести отсчет числа i}_f ^{эталонов класса в цикле f =1 уравновесивших L}_ ^{с точностью до} . ^{При этом i(f)= i}_f ^{= q}_f^{, если перед п.11} выполнялся п.7, и i(f)= i_f - 1 если перед пунктом 11 выполнялся n.10. Так как выполнялся п.7 i(f)= q_f =1 . Переходим к n.12 (I)

12. Проверяем условие P_3,f ≡ f <  Если условие выполняется перейти к п.13. Если нет - к п.14

P_3,1 ≡ 1 < 4 Условие выполняется перейти к п.13. (P₃)

13. Увеличить f на единицу перейти к п.2 (F(f))

2. Положить i_f :=1. Перейти к п.3 (O(i))

3. Из заданного подмножества E′ семейства E выделяем для

^{измерения в текущем цикле f =2 класс эталонов . Перейти к п.4 (E)}

^{4. Из выделенного класса в текущем такте i}_f ^{=1 извлекаем эталон}= e_3,1 для образования составного эталона и последующего уравновешивания выборки L_. Перейти к п.5 (Э)

^{5. Образуем составной эталон цикла f =2 такта i}_f ⁼¹

^S_f,i^=32+1*8=40

где - S_f-1 - сумма весов эталонов или вес составного эталонов или вес составного эталона используемых в уравновешивании L_ цикла f-1 c ^{точностью до S}_f-1 ^{= S}₂ ^{= 32. Перейти к п.6 (S)}

^{6. Проверяем условие если условие выполняется} переходим к п.7, если нет – к.п.9

P_1,2,1 ≡ 34 > 40 так как условие не выполняется переходим к п.9 (P₁)

9. Уменьшить i_f на единицу перейти к п.10

^{10. Возвратить эталон e}_1,1 ^{из составного веса в класс} , ^{вернувшись к предыдущему составному весу на e}_3,1 ^{меньшим. Вес эталонов использованных в цикле f =1 равен} . ^{Перейти к п. 11 (Э)}

^{11. Произвести отсчет числа i}_f ^{эталонов класса в цикле f =1 уравновесивших L}_ ^{с точностью до} . ^{При этом i(f)= i}_f ^{= q}_f^{, если перед п.11} выполнялся п.7, и i(f)= i_f - 1 если перед пунктом 11 выполнялся n.10. Так как выполнялся п.10 i(f)= 1 – 1=0 . Переходим к n.12 (I)

12. Проверяем условие P_3,f ≡ f <  Если условие выполняется перейти к п.13. Если нет - к п.14

P_3,2 ≡ 2 < 4 Условие выполняется перейти к п.13. (P₃)

13. Увеличить f на единицу перейти к п.2 (F(f))

2. Положить i_f :=1. Перейти к п.3 (O(i))

3. Из заданного подмножества E′ семейства E выделяем для

^{измерения в текущем цикле f =3 класс эталонов . Перейти к п.4 (E)}

^{4. Из выделенного класса в текущем такте i}_f ^{=1 извлекаем эталон}= e_4,1 для образования составного эталона и последующего уравновешивания выборки L_. Перейти к п.5 (Э)

^{5. Образуем составной эталон цикла f =3 такта i}_f ⁼¹

^S_f,i^=32+1*4=36

где - S_f-1 - сумма весов эталонов или вес составного эталонов или вес составного эталона используемых в уравновешивании L_ цикла f-1 c ^{точностью до S}_f-1 ^{= S}₂ ^{= 40. Перейти к п.6 (S)}

^{6. Проверяем условие если условие выполняется} переходим к п.7, если нет – к.п.9

P_1,3,1 ≡ 34 > 36 так как условие не выполняется переходим к п.9 (P₁)

9. Уменьшить i_f на единицу перейти к п.10

^{10. Возвратить эталон e}_4,1 ^{из составного веса в класс} , ^{вернувшись к предыдущему составному весу на e}_4,1 ^{меньшим. Вес эталонов использованных в цикле f =1 равен} . ^{Перейти к п. 11 (Э)}

^{11. Произвести отсчет числа i}_f ^{эталонов класса в цикле f =2 уравновесивших L}_ ^{с точностью до} . ^{При этом i(f)= i}_f ^{= q}_f^{, если перед п.11} выполнялся п.7, и i(f)= i_f - 1 если перед пунктом 11 выполнялся n.10. Так как выполнялся п.10 i(f)= 1 – 1=0 . Переходим к n.12 (I)

12. Проверяем условие P_3,f ≡ f <  Если условие выполняется перейти к п.13. Если нет - к п.14

P_3,3 ≡ 3 < 4 Условие выполняется перейти к п.13. (P₃)

13. Увеличить f на единицу перейти к п.2 (F(f))

2. Положить i_f :=1. Перейти к п.3 (O(i))

3. Из заданного подмножества E′ семейства E выделяем для

^{измерения в текущем цикле f =4 класс эталонов . Перейти к п.4 (E)}

^{4. Из выделенного класса в текущем такте i}_f ^{=1 извлекаем эталон}= e_6,1 для образования составного эталона и последующего уравновешивания выборки L_. Перейти к п.5 (Э)

^{5. Образуем составной эталон цикла f =4 такта i}_f ⁼¹

^S_f,i^=32+1*1=33

где - S_f-1 - сумма весов эталонов или вес составного эталонов или вес составного эталона используемых в уравновешивании L_ цикла f-1 c ^{точностью до S}_f-1 ^{= S}₃ ^{= 36. Перейти к п.6 (S)}

^{6. Проверяем условие если условие выполняется} переходим к п.7, если нет – к.п.9

P_1,4,1 ≡ 34 > 33 так как условие выполняется переходим к п.7 (P₁)

7. Проверяем условие P_2,f,i ≡ i_f < q_f если условие выполняется переходим к п.8, если нет – к.п.11.

P_2,4,1 ≡ 1 < 3 так как условие выполняется переходим к п.8 (P₂)

8. Увеличить i_f на единицу перейти к п.3 (F(i))

3. Из заданного подмножества E′ семейства E выделяем для

^{измерения в текущем цикле f =4 класс эталонов . Перейти к п.4 (E)}

^{4. Из выделенного класса в текущем такте i}_f ^{=2 извлекаем эталон}= e_6,2 для образования составного эталона и последующего уравновешивания выборки L_. Перейти к п.5 (Э)

^{5. Образуем составной эталон цикла f =4 такта i}_f ⁼²

^S_f,i^=32+2*1=34

где - S_f-1 - сумма весов эталонов или вес составного эталонов или вес составного эталона используемых в уравновешивании L_ цикла f-1 c ^{точностью до S}_f-1 ^{= S}₁ ^{= 34. Перейти к п.6 (S)}

^{6. Проверяем условие если условие выполняется} переходим к п.7, если нет – к.п.9

P_1,4,2 ≡ 34 > 34 так как условие не выполняется переходим к п.9 (P₁)

9. Уменьшить i_f на единицу перейти к п.10

^{10. Возвратить эталон e}_6,2 ^{из составного веса в класс} , ^{вернувшись к предыдущему составному весу на e}_6,2 ^{меньшим. Вес эталонов использованных в цикле f =4 равен} . ^{Перейти к п. 11 (Э)}

^{11. Произвести отсчет числа i}_f ^{эталонов класса в цикле f =4 уравновесивших L}_ ^{с точностью до} . ^{При этом i(f)= i}_f ^{= q}_f^{, если перед п.11} выполнялся п.7, и i(f)= i_f - 1 если перед пунктом 11 выполнялся n.10. Так как выполнялся п.10 i(f)= 2 – 1=1 . Переходим к n.12 (I)

12. Проверяем условие P_3,f ≡ f <  Если условие выполняется перейти к п.13. Если нет - к п.14

P_3,4 ≡ 4 < 4 Условие не выполняется перейти к п.14. (P₃)

14. Закончить процесс измерения. (Я)

^{I) Все значения суммы эталонов, использованных для уравновешивания} L_ с выделением S_f

,

,

,

,,

II) Результат проверки логических условий

^P_2,f,i ^{≡ i < q}_f ^P_3,f ^{≡ f < }

^P_2,1,1 ^{≡ Л(1 < 1) P}_3,1 ^{≡ И(1 < 4) P}_3,2 ^{≡ И(2 < 4)}

^P_3,3 ^{≡ И(3 < 4)}

^P_2,4,1 ^{≡ И(1 < 3)}

^P_3,4 ^{≡ Л(4 < 4)}

14) Итоги суммирования и проверки логических условий отражаем на графической процедуре измерения L_. См. рис №4

15) Представим результат измерения в виде n=6 разрядного кода в двоичной системе счисления К_ = К_2, К_2, ... К_а,. .. К_, где К_f имеет разрядность m_f и К_f - двоичный код

промежуточных разрядов К_, равный двоичному числу i_f эталонов класса в цикле f ypaвновecивших L_T.

Так как в нашем задании n=6, то К - 6-разрядный код в двоичной системе счисления. В процессе последовательного уравновешивания (процедура измерения) у нас получилось всего 4 внешних цикла, f=4, поэтому К_= К_1, К_2, К_3, К_4 .

разность равная числу двоичных разрядов кода.

при f =1 m₁=j₁ - j_1-1 = 1-0 = 1 q₁ = 2¹ – 1 = 1

при f =2 m₂=j₂ - j_2-1 = 3-1 = 2 q₂ = 2² – 1 = 3

при f =3 m₃=j₃ - j_3-1 = 4-3 = 1 q₃ = 2¹ – 1 = 1

при f =4 m₄=j₄ - j_4-1 = 6-4 = 2 q₄ = 2² – 1 = 3

где f ={1,2,3,4}

n = 1 + 2 + 1 + 2= 6, где n - разрядность двоичного кодового эквивалента значения, измеряемого параметра L_.

Количество эталонов, пошедших на уравновешивание в каждом из 4-х циклов

f₁=1

f₂=0

f₃=0

f₄=1

Теперь сводим всё выше приведенное вместе:

m₁=1 f₁=1 K_1=1

m₂=2 f₂=0 K_2=00

m₃=1 f₃=0 K_3=0

m₄=2 f₄=1 K_4=01

Записываем конечный код в двоичной системе счисления

Итак, конечный код в двоичной системе имеет вид: 100001₂. Переводим 100001₂ в десятичную систему счисления и получаем 33 (33₁₀), что соответствует заданной величине L_=34 мм с точностью х = l мм.

16) ЛСА - логическую схему алгоритма представляем в виде блок-схемы.

Общий вид алгоритма использованного в п. 13

Обозначение оператором каждого из пунктов предписания даётся в конце пункта в круглых скобках.

Начало. Переходим к п. 1 (А)

1. Положить f :=1. Перейти к п.2 (O(f))

2. Положить i_f :=1. Перейти к п.3 (O(i))

3. Из заданного подмножества E′ семейства E выделяем для

^{измерения в текущем цикле f =1 класс эталонов . Перейти к п.4 (E)}

^{4. Из выделенного класса в текущем такте i}_f ^{=1 извлекаем эталон} для образования составного эталона и последующего уравновешивания выборки L_. Перейти к п.5 (Э)

^{5. Образуем составной эталон цикла f =1 такта i}_f ⁼¹

^S_f,i^=0+1*8=8

где - S_f-1 - сумма весов эталонов или вес составного эталонов или вес составного эталона используемых в уравновешивании L_ цикла f-1 c ^{точностью до S}₀ ^{= 0. Перейти к п.6 (S)}

^{6. Проверяем условие если условие выполняется} переходим к п.7, если нет – к.п.9 (P₁)

7. Проверяем условие P_2,f,i ≡ i_f < q_f если условие выполняется переходим к п.8, если нет – к.п.11. (P₂)

8. Увеличить i_f на единицу перейти к п.3 (F(i))

9. Уменьшить i_f на единицу перейти к п.10