1.5. Мех. И эл.Мех. Характеристики асинхронного двигателя.
Статические св-ва АД изучаются на основе эквивалентной схемы рис.3.53. Эта эквивалентная схема справедлива для любой фазы симметричного многофазного АД.
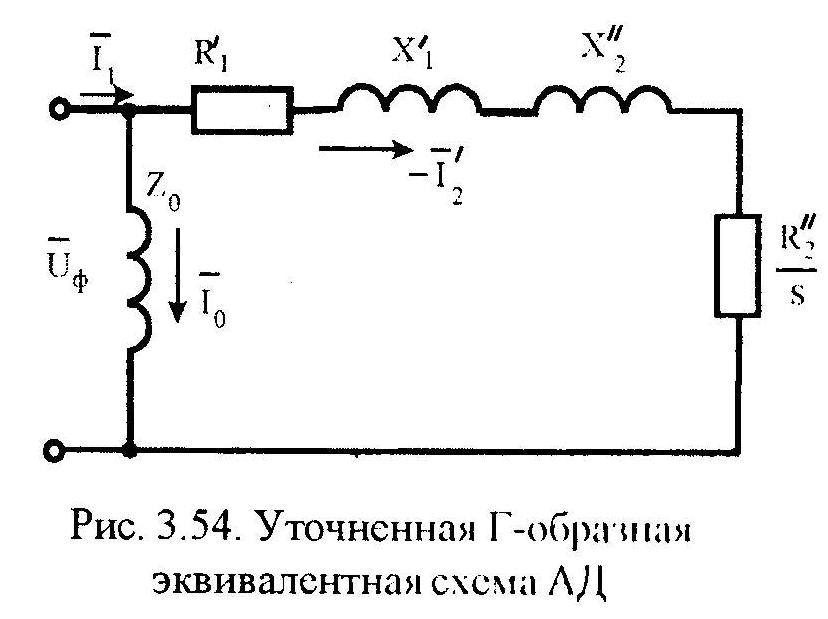
Для удобства экв. Т- схему рис.3.53 преобр. в экв. Г-образную схему с вынесенным на зажимы источника питания намагн. контуром (без учета потерь в стали) – рис.3.54.
П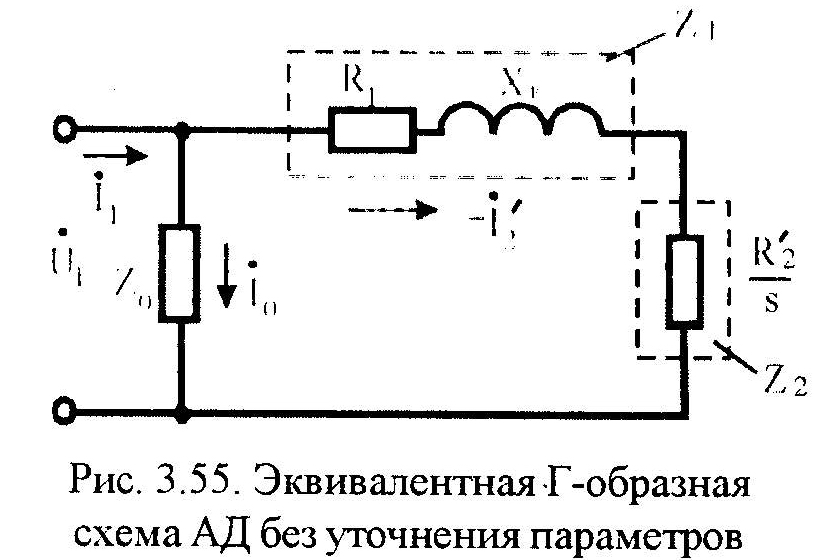
ри
этом параметры Г-образной схемы изменяются
согласно соотношениям:
(3.224)
где
(3.225)
В ТЭП при питании АД от сети с неизменной частотой в используют упр. Г- схему, принимая 1 = 1, т. е. корректировку параметров не производят. с целью выяснения основных свойств и характеристик АД мы принимаем это допущение. В результате получаем эквивалентную схему, приведенную на рис.3.55.
В соответствии с рис.3.55 определяем приведенный ток фазы ротора
(3.226)
где
(3.227)
Хк
– инд. сопр. КЗ АД.
(3.228)
В то же время эл.магн. мощ., прох. через воздушный зазор АД, может быть выражена через произведение эл.магн. момента М и синхронной угловой скорости о :
(3.229)
следовательно,
эл.магн. момент АД
(3.230)
Мах эл.магн. М, передаваемой в АД, будет тогда, когда “внутреннее сопротивление источника” Z1 будет равно сопротивлению “нагрузки” Z2 (см. рис.3.55), т. е. Z1 = Z2 или
(3.231)
откуда
(3.232)
где sк – критическое скольжение АД.
Можно
приведенный ток ротора
,
соответствующий sк
:
(3.233)
Эл.магн.
мощ. Рэм, к
, соотв. sк
:
(3.234)
Соотв.
критический эле.магн. М АД:
(3.235)
В (3.232) (3.235) знак плюс относится к дв. режиму, а знак минус – к ген. при о .
Взяв отношение (3.230) к (3.235), можно получить формулу Клосса:
(3.236) где
(3.237)
Обычно
критический М выражают в долях от ном.
для дв. реж.
(2.238)
Введя
безразмерную величину эле.магн. момента
(3.239)
и
отн. скорость
(3.240)
получим
выражение мех. хар-ки АД в безразмерных
величинах
(3.241)
для дв. реж. 01, для ген. рекуп. реж. 1<<, для реж. противовк. -0
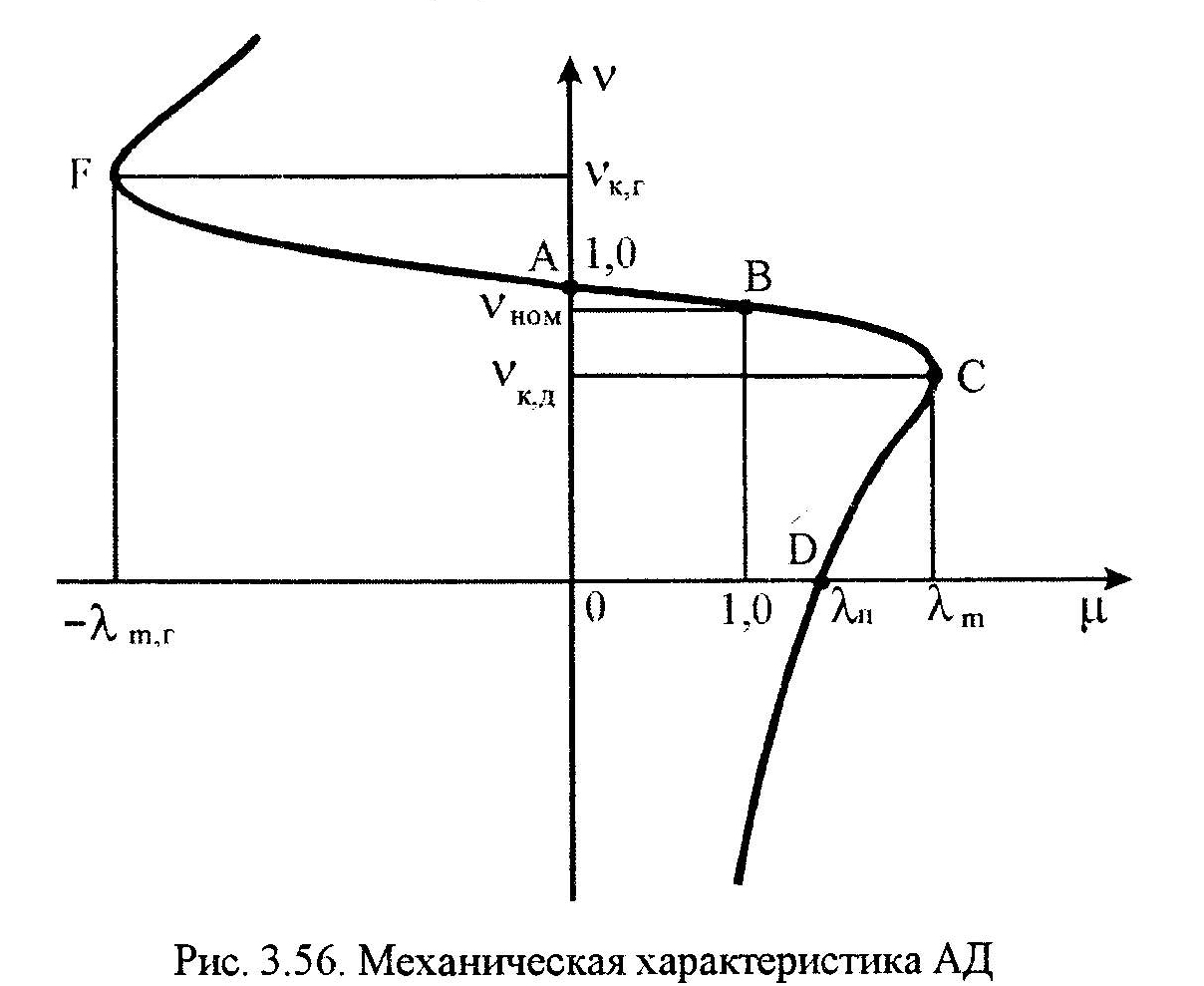
На мех. хар-ке рис.3.56 можно отметить характерные точки:
точка А(=1,=0) – режим идеального холостого хода, или синхронной скорости,
точка В(=ном,=1) – номинальный режим,
точка С(=к,д,=м) – режим критической скорости в двигательном режиме,
точка D(=0,=п) – режим пуска АД,
точка F(=к,г,=т,г) – режим критического генераторного момента.
Для
ЭД большой мощ. можно принять R1=0,
тогда a=0 и из (3.241) получаем
упрощенную формулу механической
характеристики АД в безразмерных
величинах:
(3.242) где sк=
(3.243)
(3.244)
Асинхронный двигатель характеризуется также полной механической мощностью
,
Кот.
достигает мах
при
скольжении
,
которое меньше критического скольжения sк. Величина Pмх,max уменьшается с увеличением критического скольжения. Можно видеть, что в точках идеального хх (0,w0) и пускового момента (Mп,0) полная механическая мощность равна нулю.
Влияние параметров на механическую характеристику АД
Влияние параметров на мех. хар-ку АД будем оценивать через критический момент (3.235), критическое скольжение (3.232) и скорость ротора
(3.235)
(3.232)
:
1)
Очевидно,
что критическое скольж. не меняется,
следовательно, крит. скор.
,
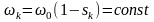а крит. М пропорц. квадрату напр. Хар-ки
показаны на рис.3.59.
2)
С увеличением R1 (или X1) критическое скольжение уменьшается, критическая скорость wk увеличивается, а критический момент уменьшается (рис.3.60).
3)
Крит.
М не изм., а крит. скольжение изменяется
пропорционально
(рис.3.61).
4
)
Д
ля
оценки влияние изм. частоты, примем во
внимание, что
,
.
При
R1=0 имеем
,
т.е. синхронная скор. АД увеличивается
пропорц. увел. частоты, критическое
скольж. уменьшается обратно пропорц.
частоте, а крит. момент уменьшается
обратно пропорционально квадрату
частоты (рис.3.62).
Уменьшать
частоту при
нельзя, так как это приведет к увеличению
магн. потока Фm и
чрезмерному насыщению магн. системы
дв. С уменьш. f1
необходимо одновременно уменьшать и
напряжение U1 , чтобы
насыщение машины находилось в допустимых
пределах.
ЭЛ.МЕХ. ХАР-КИ АД.
В
связи с тем, что при скольж., большем
крит., ток АД продолжает возрастать, а
М начинает уменьшаться, для АД важна
эл.мех. хар-ка, выражаемая через ток
ротора и статора
Для
тока ротора I
эта хар-ка имеет параметрическое в-ние:
Для
(3.249) имеем характерные точки (рис. 3.57,
сплошная кривая):
s=0;
;
w=w0;
s=-
;
;
w=w0(1+
);s=1;
;
w=0; s;
;
w.
Получить зависимость w=f(I1) можно, преобразуя Т-образную эквивалентную схему рис. 3.53 в схему с последовательным соединением комплексных сопротивлений (рис.3.58).
Обозначим:
(3.250)
тогда “внутреннее” комплексное сопротивление АД
(3.251)
При подстановке (3.250) в (3.251) и последующих преобразованиях находим:
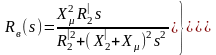(3.252)
Эквивалентное сопротивление цепи АД при данном скольжении s:
, (3.253)
где
(3.254)
Ток статора I1 при данном скольжении s определяется как
,(3.255)
а скорость ротора w=w0(1-s).
Рассмотрим характерные точки для (3.255):
s=0; Rв(s)=0; RАД=R1;Xв(s)=X; XАД=X1+X.
.s; Rв(s)0; Xв(s)
;.
RАД=R1;
.
.
s=1;
;
;
RАД=R1+Rв;
XАД=X1+Xв;
Приближенно действующее значение тока статора АД можно определить по формуле профессора В.А.Шубенко:
(3.256)
где
. (3.257)
– скольжение на
расчетной (искусственной) характеристике
при M=Mном,
M,s – текущие значения электромагнитного момента и скольжения.
Критическое скольжение можно найти, решая уравнение (3.241) при =ном и =1:
,(3.258)
где
При R1=0 (a=0) уравнение (3.258) принимает вид:
(3.259)Ток холостого
хода АД можно определить и по другой,
более простой эмпирической формуле
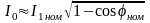(3.260)