1.1 Приведение моментов сопротивления и сил, моментов инерции и масс к валу электродвигателя. Учёт потерь в передачах.

Многомассовая система (рис. 1.14 а) приводится к одномассовой системе (рис. 1.14 б), имеющей суммарный J, Мс, угловую скорость ω и угол поворота вала φ.

На основании закона сохранения энергии имеем равенство: Мс ω = М_М ω_Н, (1.78)

т огда статического Мс (приведенного ) момента

При поступательном движении исполнительного механизма (рис. 1.15 а):

Мс ω = Fс (1.80) где – линейная скорость механизма; Fc – сила сопротивления в установившемся движении; Мс – эквивалентный статический момент на валу двигателя одномассовой системы (рис. 1.15 б).

Из (1.80) получаем

, (1.81) где ρ – радиус приведения поступательного движения к вращательному.

Для линейных передаточных механизмов (j=const, ρ=const) рассмотрим приведения моментов инерции и масс к валу электродвигателя. При вращательном движении исполнительного механизма (см. рис. 1.14 а) и идеальном ПМ кинетическая энергия неприведенной системы должна равняться кинетической энергии приведенной системы (см. рис. 1.14 б), т.е.

, (1.80) Откуда находим суммарный момент инерции приведенной системы:

(1.81) где (1.82)

– приведенный к валу электродвигателя момент инерции механизма.

Для поступательного движения исполнительного механизма (см. рис. 1.15а) записываем равенство кинетических энергий приведенной и неприведенной систем: (1.83), из которого получаем (1.84), где (1.85)

– приведенный к валу электродвигателя момент инерции поступательно движущейся массы m; – момент инерции ротора электродвигателя; – момент инерции барабана, соединенного с ротором ЭД.

Приведение сил, моментов сопротивления, моментов инерции и масс к валу ЭД для нелинейных ПМ

Н а примере кривошипно-шатунного механизма (рис. 1.16).

Пренебрегаем потерями в кривошипно-шатунном механизме и массой его элементов.По закону сохранения энергии

F_В = F_A , (1.86)

откуда

F_A= F_В , (1.87)

Где =ω_К·r, (1.88)

(1.89)

– линейная скорость точки А; ω_К – угловая скорость кривошипа АО; r – радиус кривошипа; ω – угловая скорость ротора электродвигателя; j – передаточное число ПМ.

Поскольку при ω_К=const скорость ползуна В изменяется как по величине, так и по направлению при изменении угла поворота φ кривошипа ОА, то и сила в точке А будет функцией угла, т.е. F_A=F(φ). Момент силы F_A относительно точки О

M_O(F_A)= F_A·r= F_В·r· =М_М (1.90) Статический момент на валу электродвигателя в соответствии с (1.79): (1.91)

Обозначим m_B как массу ползуна и перемещаемого им изделия. Тогда кинетическая энергия движущейся массы m_B будет равна W_B=m_B (1.92)

Приведем эту кинетическую энергию в точку А с фиктивной массой m_A, имеющей линейную скорость : m_B = m_A (1.93); m_A=m_B (1.94)

Момент инерции точечной массы m_A относительно оси О по определению равен J₀(m_A)=J_M= m_Ar²=m_Br² (1.95)

Приведение этого момента инерции к валу электродвигателя выполняется в соответствии с правилом (1.82): (1.96)

Для аналитического определения Мс и необходимо найти отношение . С этой целью воспользуемся следствием одной из теорем теоретической механики: при плоском движении проекции скоростей двух точек на прямую, проходящую через эти точки, равны, т.е. _(АВ) = _(АВ) (1.97)

Как следует из рис. 1.16: cosβ= sin(φ+β),(1.98) тогда (1.99)

Или (1.200)

Для треугольника ОАВ (рис. 1.16) по теореме синусов имеем

Откуда (1.201)

Подставим (1.201) в (1.200), получим (1.202)

Теперь можно записать аналитическое выражение для приведенного к валу электродвигателя момента сопротивления

(1.203)и момента инерции

(1.204)

которые являются функцией угла поворота φ кривошипа ОА.

Момент инерции передаточного механизма в большинстве своем неизвестен, поэтому его принимают равным (10-30)% от момента инерции ротора электродвигателя, т.е.

J_ПМ=(0,1÷0,3)J_Д (1.205)

В общем случае суммарный момент инерции электропривода, приведенный к валу электродвигателя, вычисляются по формуле: J=(1,1÷1,3)J_Д+ (1.206)

УЧЕТ ПОТЕРЬ В ПЕРЕДАЧЕ.

Потери энергии (мощности) в передаче учитывают двумя способами:

1) приближенным, т.е. с помощью КПД и 2) уточненным, т.е. непосредственным вычислением составляющих потерь. Рассмотрим эти способы.

А. Учет потерь в передачах с помощью КПД.

Механическая часть электропривода (рис.1.17) включает ротор электродвигателя ЭД с угловой скоростью w и моментом М, передаточный механизм ПМ, имеющий КПД h_п и передаточное число j, и исполнительный механизм ИМ, на валу которого приложен момент М_м и скорость вала w_м. Для наглядности обозначим статический момент в двигательном режиме , а в тормозном - . Для двигательного режима работы, исходя из закона сохранения энергии, можно записать равенство

, , где ,

- момент механизма, приведенный к валу электродвигателя.

Для тормозного режима будем иметь такое равенство

, ,

Но КПД является переменной величиной, зависящей от постоянных и переменных потерь в передаче. Определим потерю момента в передаче для двигательного режима

,

Примем допущение, что в тормозном режиме будет такая же потеря момента. Тогда статический момент в тормозном режиме можно записать в таком виде:

1) , тогда , что соответствует тормозному режиму, когда двигатель развивает тормозной момент. Применительно к грузоподъемному механизму это будет опускание тяжелого груза, когда момент от действия груза на валу двигателя М_г превышает момент потерь М в передаче. Получаем так называемый тормозной спуск;

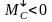2) , тогда , что соответствует не тормозному, значит, двигательному режиму. Для грузоподъемного механизма это эквивалентно опусканию крюка, когда момент от его веса на валу двигателя М_К меньше момента потерь М в передаче. Имеем так называемый силовой спуск.

Потери момента в передаче приближенно выражаются через две составляющие, одна из которой для данной передачи является постоянной величиной, а вторая – пропорциональна передаваемому моменту: ,

где – коэффициент постоянных потерь;

b – коэффициент переменных потерь;

М_с.ном – номинальный статический момент передачи;

М_перед – передаваемый момент, который равен моменту на выходном (по направлению передачи энергии) валу передачи.

Для установившегося двигательного режима . КПД передачи можно представить отношением мощностей в установившемся режиме:

,

где , ,

P₂ – мощность на выходном валу ПМ в установившемся двигательном режиме;

P – потери мощности в передаче.

, Обозначим , ,

При номинальной нагрузке К_З=1 и

, ,

Таким образом, КПД передачи является функцией коэффициента загрузки и номинального КПД, так как коэффициент постоянных потерь зависит от номинального КПД и для ряда передач приводится в справочниках.

1.2. ВРЕМЯ РАЗГОНА И ТОРМОЖЕНИЯ ЭЛЕКТРОПРИВОДА. ОПТИМАЛЬНОЕ ПЕРЕДАТОЧНОЕ ЧИСЛО РЕДУКТОРА.

Пологая в общем случае, что динамический момент является функцией

скорости, т. е. М_дин(), время переходного процесса t_п.п. при изменении скорости от ₁ до ₂ находим из основного уравнения движения электропривода (1.72) (1.72): . (1.325)

Интеграл в (1.325) можно взять только для частных случаев функции М_дин():

а) М_дин() = М_дин = const, в этом случае

, (1.326) где .

б) М_дин = , тогда

. (1.327)

Поскольку эл.мех. постоянная времени T_M оперделяется как , то время переходного процесса лучше предствить в виде двух формул в зависимости от знака жёсткости динамического момента.

, при  > 0 (1.328) , при b < 0 (1.329)

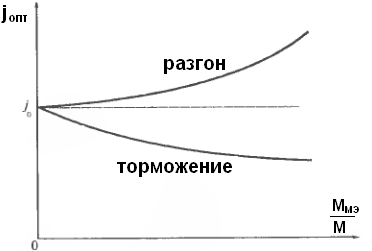
ОПТИМАЛЬНОЕ ПЕРЕДАТОЧНОЕ ЧИСЛО РЕДУКТОРА

1. По минимуму времени переходного процесса:

1. первый способ: (ЭД М=const, Jд=const) (Исполн-й мех-м Mн,wн,Jн)

+ торможение , - разгон

При оптимальном j и отсуствия момента нагрузки на валу, кинетическая энергия механизма = кинетической энергии ЭД вместе с редуктором

2. второй способ (ЭД P =const) (Исполн-й мех-м Mн,wн,Jн)

М=const; М=Мном ;

ОПТИМАЛЬНОЕ ПЕРЕДАТОЧНОЕ ЧИСЛОПО КРИТЕРИЮ минимум габарита ЭД

угловое ускорение:

при отсуствии нагрузки на выходном валу _,

фиктивный момент инерции ,

тогда следовательно