3.4. Рабочая диаграмма термодинамического процесса

Диаграмма, указанная в названии темы, строится в системе координат <v, р>. Для ее изображения используется выражение, описывающее работу расширения газа. Выше был получен результат –

dl = p·dv.

Отсюда следует, что

l = f (p, v).

Из диаграммы, приведенной на рис. 10, ясно, что общая удельная работа определяется интегрированием выражения для dl в пределах v_н, v_к –

l v_к v_к

∫dl = ∫p·dv = ∫p(v)·dv.

0 v_н v_н

Рабочая диаграмма применяется для наглядного представления количества работы в изучаемом термодинамическом процессе. Любой политропный процесс можно графически интерпретировать в координатах <v, р>.

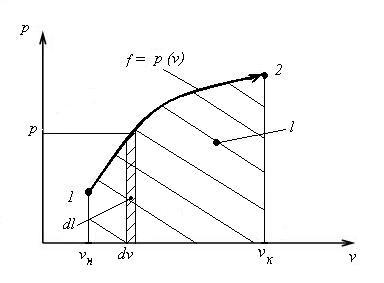
Рис. 10. Пример рабочей диаграммы термодинамического процесса

3.5. Выражение первого закона термодинамики для работы расширения газа

Учитывая равенство для элементарной работы расширения газа

dl = p·dv,

первый закон термодинамики легко можно записать в виде –

dq = du + p·dv.

Необходимо отметить, что последнее уравнение в соответствующих эквивалентных формах применимо для количественных оценок любых энергетических процессов.

3.6. Работа изменения давления (располагаемая работа рабочего тела)

Работа изменения давления РТ непосредственно связанна с энергией проталкивания. Элементарное выражение указанной работы записывается в виде –

dl_p = – v·dp. [Дж/кг]

Нужно подчеркнуть, что здесь знак “минус” соответствует положительному значению работы. Действительно, этот знак говорит об уменьшении давления РТ, что эквивалентно увеличению его объема; таким образом, расширяясь, РТ совершает работу над ОС. Очевидно (см. рис. 11), что –

р_к

l_p = ∫v∙dp. [Дж/кг]

р_н

3.7. Модифицированный вид первого закона термодинамики

При исследовании проталкиваемого РТ удобнее использовать не основной вид первого закона термодинамики –

dq = du + p·dv,

а модифицированный. Чтобы его получить, нужно найти дифференциал энергии проталкивания –

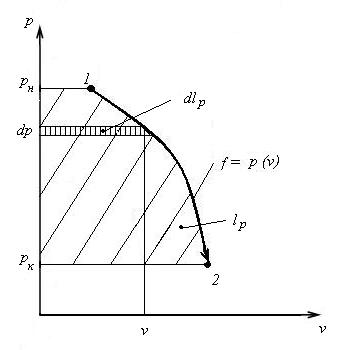
Рис. 11. Иллюстрация к выводу формулы для располагаемой работы РТ

e_пр = p·v.

Этот дифференциал равен –

d(p·v) = p·dv + v·dp.

Последнее уравнение можно разрешить относительно работы расширения газа –

p·dv = d(p·v) – v·dp.

Подставив найденный ответ в уравнение для первого закона термодинамики, получим

dq = du + d(p·v) – v·dp.

Известно, что энтальпия рабочего тела равна

i = u + p·v.

Тогда

dq = d(u + p·v) – v·dp

и окончательно –

dq = di – v·dp. [Дж/кг]

Естественно, что оба уравнения, основное и модифицированное, описывающие первый закон термодинамики, равноценны. Но требуется отметить, что с методической точки зрения первое удобнее применять к неподвижному газу (РТ), а второе – к подвижному.

Вспомним, что элементарное выражение положительной располагаемой работы имеет вид –

dl_p = – v·dp.

Таким образом, модифицированное уравнение первого закона термодинамики можно преобразовать в форму

dq = di + dl_p.