4.5. Понятие об изохорной и изобарной удельных теплоемкостях

На практике значительную роль играют удельные теплоемкости при постоянных объеме с_v и давлении с_р. Эти характеристики для большинства рабочих тел исследованы, т.е. получены зависимости c = f (T) и с^-= f (∆T), которые приведены в справочной литературе. По известным значениям изохорной и изобарной удельных теплоемкостей можно определить удельную теплоемкость с для любого вида политропного процесса.

Изохорную удельную теплоемкость РТ определяют из эксперимента, при проведении которого не меняется удельный объем РТ v, а изобарную – из опыта, когда давление РТ p остается постоянным.

4.6. Связь между изохорной и изобарной удельными теплоемкостями

Рассмотрим изохорный и изобарный процессы нагрева РТ в ТДС “цилиндр-поршень-рабочее тело” (рис. 13).

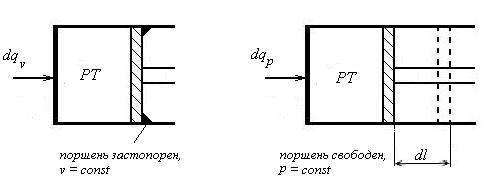
Рис. 13. Изохорный и изобарный процессы нагрева РТ

В том случае, когда v = const, при нагревании растут давление и температура РТ –

c_v = dq_v/dT. [Дж/(кг·К)]

Если р = const, при нагревании возрастают температура и удельный объем РТ, а поршень движется, т.е. совершается еще и работа dl. Здесь –

с_р = dq_p/dT. [Дж/(кг·К)]

Из условия проведения опытов следует, что удельная теплота dq_v расходуется только на нагрев РТ на величину dT, а dq_p – на нагрев на ту же величину dT (изменение внутренней энергии РТ) и совершение работы dl. Таким образом, в первом и втором случаях нагрев неэквивалентен, причем всегда dq_p > dq_v. Иными словами, c_p > c_v, как уже отмечалось выше.

Связь между c_p и с_v выражается не только упоминавшимся и приводившимся уравнением Майера

с_р – с_v = R,

но и через коэффициент Пуассона γ = c_p/с_v.

Выразим с_р через с_v и γ –

с_р = γ·с_v,

а результат подставим в уравнение Майера.

Получим –

γ·с_v – с_v = R.

Отсюда можно вывести два равенства, которые широко используются в термодинамических расчетах –

с_v = R/(γ – 1) и с_р = γ·R/(γ – 1).

4.7. Общее расчетное выражение удельной теплоемкости

Для каждого политропного процесса его удельная теплоемкость является функцией показателя политропы n, коэффициента Пуассона γ и удельной изохорной теплоемкости, т.е. с = f (n, γ, с_v). Можно показать, что –

c = c_v·(n – γ)/(n – 1). [Дж/(к∙К)]

4.8. Теплоемкость сложного рабочего тела (смеси)

Удельная теплоемкость является аддитивной величиной, т.е. обладает свойством независимости. Соответственно суммарную теплоемкость смеси газов (например, воздуха и продуктов сгорания авиационного топлива) можно определить как алгебраическую сумму, учитывающую долю каждого компонента изучаемой смеси.

Массовую долю суммы принято обозначать g –

n

g = ∑ g_i = 1,

i = 1

где n – количество компонентов смеси, g_i – массовая доля каждого компонента.

Расчетное выражение для суммарной теплоемкости сложного РТ имеет вид –

n

c_∑ = ∑ c_i·g_i,

i = 1

где c_i – удельная теплоемкость i-того компонента смеси. Размерностью c_∑ служит [Дж/(кг∙К)].

Иногда в справочной литературе наряду со значениями с удельных теплоемкостей рабочих тел, приведенных к единице массы, указываются величины, отнесенные к единице количества вещества ([моль], [кмоль]). В этих случаях теплоемкость обозначают большой латинской буквой С, а единицами ее измерения являются [Дж/(моль·К)] и [Дж/(кмоль·К)]. Учитывая размерности, от С легко перейти к с –

с = С/µ,

где µ – молярная масса РТ.

В практических расчетах необходимо принимать во внимание, относятся справочные данные к изобарной или изохорной теплоемкости РТ, истинной или средней теплоемкости. При решении задач необходимо переходить к средней удельной теплоемкости, отнесенной к единице массы.