4. Классификация запасов находящихся на складе с использованием метода аbc

Задача 4. Рассчитать необходимое количество запасов, классифицировать их с использованием метода АВС по стоимостному показателю и построить графическую зависимость в % соотношении (стоимость – количество). Исходные данные приведены в Приложении 3.

Методика и решение. В любой момент времени в системе материально-технического снабжения обычно имеются определенные запасы, движущиеся из одной части этой системы в другую.

Запасы - материальные ценности, ожидающие производственного или личного потребления, форма существования материального потока, имеющая место в определенное время в определенном месте.

Для определения среднего количества товарно-материальных запасов в системе материально-технического обеспечения используется следующая формула:

Q_з= ∑Q_зi= ∑S_i*T_i, (4.1)

где, Q_з — общий объем товарно-материальных запасов;

S — средняя норма потребления этих запасов на заданный период времени;

Т — среднее время транспортировки.

Рост ассортимента запасов стал отправной точкой для создания методов их систематизации и группировки. Для распределения запасов в зависимости от количества и стоимости воспользуемся методом АВС.

Метод АBC - способ формирования и контроль над состоянием запасов, заключающийся в разделении, группировке объектов N реализуемых ценностей по степени влияния на общий результат на три неравных подмножества A, B, C.

Как правило, решение такой задачи включает четыре этапа:

• первый: определить объекты анализа (номенклатурная единица (запасы), клиент, поставщик, товарная группа/подгруппа и т.п.);

• второй: определить параметр, по которому будет проводиться анализ объекта (средний запас, руб.; объем потребления, руб.; доход, руб.; количество единиц, шт.; количество заказов, шт. и т.п.);

• третий: сортировка объектов анализа в порядке убывания значения параметра.

• четвертый: определение групп А, В и С.

Для определения принадлежности выбранного объекта к группе необходимо:

1. Рассчитать долю параметра от общей суммы параметров выбранных объектов.

2. Рассчитать эту долю с накопительным итогом.

3. Присвоить значения групп выбранным объектам.

К группе А относят немногочисленные виды запасов, но на них приходится преобладающая часть денежных средств, - это особая группа с точки зрения определения величины заказа, контроля текущего запаса, затрат на доставку и хранение.

К группе В относят запасы, занимающие среднее положение в формировании запасов склада, они требуют меньшего внимания, за ними производится обычный контроль.

Группа С включает запасы, составляющие большую часть, на них приходится незначительная часть финансовых средств, как правило, за позициями группы С не ведется постоянный учет – проверка осуществляется периодически.

В табл. 4.1 приведены материалы, отражающие процентное соотношение групп А, В, С.

Таблица 4.1

Процентное соотношение групп А, В, С

Источник	Группа А		Группа В		Группа С
	УА	ХА	УВ	ХВ	УС	ХС
А.М. Гаджинский	75	10	20	20	5	70

Для решения поставленной задачи необходимо составить таблицу, в которой все номенклатурные позиции расставляются по стоимостному показателю:

C_i = n_i*Ц_{i ,} (4.2)

где n_i – количество единиц i-той продукции, ед.;

Ц_i - стоимость единицы i-той продукции, руб./ед.

Данные о 20 позициях продукции представлены в табл. 4.2.

Таблица 4.2

Исходные данные
№	ni, ед.	цi, руб./ед.	ci, руб.	Si, ед. /мес.	Ti, час
1 плинтус	5	20	100	5	2
2 гофрированный лист	35	50	1750	7	2
3 кисть	20	2	40	10	5
4 замок	1	30	30	1	15
5 ламинат	12	500	6000	10	24
6 краска	40	5	200	25	17
7 блоки	4	200	800	3	12
8 шпатель	2	3	6	2	15
9 арматура	4	100	400	4	11
10 линолеум	12	700	8400	8	10
11 клей для ламината	10	4	40	7	7
12 цемент	18	150	2700	10	5
13 щиты	12	350	4200	5	3
14 крепеж	43	45	1935	40	9
15 стеклопакеты	37	1000	37000	35	4
16 подложка для ламината	13	40	520	5	6
17 крепежный набор для пласт. плинтусов	1	130	130	1	8
18 дверь	7	255	1785	7	7
19 сварочный шнур	24	200	4800	20	5
20 клей для линолеума и ковролина	3	4	12	2	3
Сумма	303		70848

После расчета полученные значения показателей стоимости располагаются в порядке убывания.

С₁≥С₂≥……….С_i≥…….С_N , (4.3)

где N – общее количество наименований (объем выборки).

Произведем распределение на группы дифференциальным способом, опирающимся на среднее значение показателя.

(4.4)

Граничные значения С_А и С_В рассчитываются с помощью коэффициентов К_i, величины которых принимаются равными К₁=6, К₂=0,5 по данным Маликова О.Б., 2003.

К группе А относятся запасы, показатели которых

С_i≥К₁*

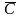(4.5)

К группе В относятся запасы, показатели которых

К₁*

>С_j≥ К₂*

(4.6)

К группе С относятся

К₂*

> С_l (4.7)

Для удобства расчетов производим нормирование стоимостных q_i и количественных n_i показателей (в процентах %). Количественные показатели нормируются аналогично стоимостным.

q_i=100*С_i/Q, (4.8)

где Q=

(4.9)

Величина q_j и n_j суммируется нарастающим итогом:

q_j=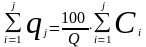 (4.10)

Среднее значение показателя С=70848/20=3542,4 руб. В группу А войдут позиции, для которых величина С больше или равна 21254,4 руб. К группе B относятся позиции меньше 21254,4 и больше 1771,2 руб. И все остальные запасы к группе C. Результаты расчетов сведены в табл. 4.3.

Таблица 4.3

Исходные данные				Результаты обработки																	Группа
№	ni, ед.	цi, руб. /ед.	Ci, руб.	Si, ед. /мес.	Ti, час		№		№,		ni,%		∑nj %		Ci		qi,%		∑qj, %
1	5	20	100	5	2		1		15		12,21		12,21		37000		52,22		52,22		А
2	35	50	1750	7	2		2		10		3,96		16,17		8400		11,86		64,08		В
3	20	2	40	10	5		3		5		3,96		20,13		6000		8,47		79,32
4	1	30	30	1	15		4		19		7,92		28,05		4800		6,78		79,32
5	12	500	6000	10	24		5		13		3,96		32,01		4200		5,93		85,25
6	40	5	200	25	17		6		12		5,94		37,95		2700		3,81		89,06
7	4	200	800	3	12		7		14		14,19		52,15		1935		2,73		91,80
8	2	3	6	2	15		8		18		2,31		54,46		1785		2,52		94,31
9	4	100	400	4	11		9		2		11,55		66,01		1750		2,47		96,78		С
10	12	700	8400	8	10		10		7		1,32		67,33		800		1,13		97,91
11	10	4	40	7	7		11		16		4,29		71,62		520		0,73		98,65
12	18	150	2700	10	5		12		9		1,32		72,94		400		0,56		99,21
13	12	350	4200	5	3		13		6		13,20		86,14		200		0,28		99,49
14	43	45	1935	40	9		14		17		0,33		86,47		130		0,18		99,68
15	37	1000	37000	35	4		15		1		1,65		88,12		100		0,14		99,82
16	13	40	520	5	6		16		11		3,30		91,42		40		0,06		99,88
17	1	130	130	1	8		17		3		6,60		98,02		40		0,06		99,93
18	7	255	1785	7	7		18		4		0,33		98,35		30		0,04		99,97
19	24	200	4800	20	5		19		20		0,99		99,34		12		0,02		99,99
20	3	4	12	2	3		20		15		0,66		100,00		6		0,01		100,00
Сумма	303		70848	20	170												100		100
				Qз =1751

Построим кривую Лоренца, которая характеризует кумулятивное возрастание величин двух взаимосвязанных признаков (в % к итогу), и показывает степень концентрации отдельных элементов по группам.

На оси ординат наносятся значения q_j, на оси абсцисс – значения n_j, соответствующие присвоенным номерам позиций запасов. Точки с координатами (n_j; q_j)

Для исследуемых обычно соотношений количества и стоимости этот анализ приводит к следующим результатам: небольшое количество наименований (деталей, материалов и др.) составляет большую часть стоимости, для большого количества наименований эта доля стоимости относительно мала (рис. 4.1).

Рис. 4.1 Взаимосвязь между количеством и стоимостью

Таким образом, 12 % запасов составляют 52 % стоимости (группа А), 42 % – 42 % (группа В), 46 % - 6 % (группа С).

Поэтому для запасов группы А необходимо особенно точно рассчитывать потребность; оптимальную величину заказа; а состояние запасов следует тщательно контролировать.