9.5.2. Бинарные деревья
Бинарные деревья – это деревья, состоящие из узлов, каждый из которых имеет 0, 1 или 2 потомков. Таким образом, каждый из узлов бинарного дерева состоит из 3 полей: поля данных и 2 указателей на левое и правое поддеревья. Указатели листовых элементов имеют значение NULL.
На рис. 9.10 представлено бинарное дерево, каждый узел которого включает поле данных типа int, указатель на левое поддерево leftPtr и указатель на правое поддерево rightPtr. Указатель на корень дерева – rootPtr.
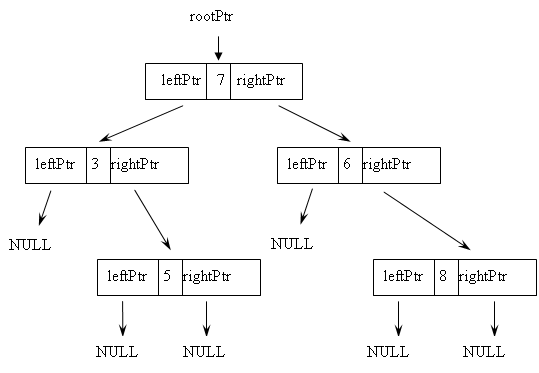
Рис. 9.10. Бинарное дерево
В программировании большое значение имеют деревья бинарного поиска. Они имеют свою характерную особенность, заключающуюся в том, что, если указатель на левое поддерево отличен от NULL, то значение в корне левого поддерева меньше значения в данном корневом узле, и, если указатель на правое поддерево отличен от NULL, значение в корне правого поддерева больше данного значения (рис. 9.11).
Рис. 9.11. Бинарное дерево двоичного поиска
Бинарные деревья поиска очень важны в качестве структур данных, так как они позволяют хранить большие объемы данных и в то же время обеспечивают быстрый и эффективный доступ к ним. Время поиска в бинарном дереве по сравнению с линейным поиском уменьшается с n до log2n.
Структура, описывающая бинарное дерево.
struct Tree
{
int root;
struct Tree *leftPtr;
struct Tree *rightPtr;
};
К бинарным деревьям применим ряд примитивных операций:
// Возвращает значение информационного поля узла inp
int info(struct Tree *inp)
{
return inp->root;
}
// Возвращает указатель на правое поддерево узла inp
struct Tree *rightS(struct Tree *inp)
{
return inp->rightPtr;
}
// Возвращает указатель на левое поддерево узла inp
struct Tree *leftS(struct Tree *inp)
{
return inp->leftPtr;
}
// Возвращает указатель на корневой узел
// (узел-отца) для узла inp
struct Tree *father(struct Tree *inp)
{
if (inp == head)
return head;
struct Tree *p = head, *q;
do
{
q = p;
if ((p) && (info(p) <= info(inp)))
p = rightS(p);
else
p = leftS(p);
}
while (info(p) != info(inp));
return q;
}
// Возвращает указатель на узел-брата для узла inp,
// т.е. указатель на отличный от inp корень поддерева
// с тем же узлом-отцом
struct Tree *brother(struct Tree *inp)
{
struct Tree *fath = father(inp);
if (rightS(fath) == inp)
return rightS(fath);
else
return leftS(fath);
}
// Возвращает 1, если inp указывает на корень
// левого поддерева, иначе 0
int isLeft(struct Tree *inp)
{
struct Tree *fath = father(inp);
if (leftS(fath) == inp)
return 1;
else
return 0;
}
// Возвращает 1, если inp указывает на корень
// правого поддерева, иначе 0
int isRight(struct Tree *inp)
{
struct Tree *fath = father(inp);
if (rightS(fath) == inp)
return 1;
else
return 0;
}
Основными функциями при работе с деревьями являются функции вставки узлов, трех обходов и удаления узлов дерева.
С помощью описанной ниже функции можно создать бинарное дерево двоичного поиска, представленное на рис. 9.11. Функция получает в качестве одного из параметров указатель на начало дерева.
// Функция добавления узла в бинарное дерево двоичного поиска
typedef Tree *TreePtr;
void insertTree(TreePtr *RootPtr, int value)
{
TreePtr newPtr;
if (*RootPtr == NULL) //если указатель на корень пуст
{
//выделение памяти под новый элемент
newPtr = (Tree *) malloc(sizeof(Tree));
if (newPtr != NULL)
{
newPtr->root = value;
newPtr->leftPtr = NULL;
newPtr->rightPtr = NULL;
}
*RootPtr = newPtr; // присваивание указателю на пустое
// поддерево значения указателя
// на новый элемент
}
else
if (value < info(*RootPtr))
// иначе, если вставляемый элемент меньше корня
// поддерева, рекурсивно перемещаемся в левое поддерево
insertTree(&((*RootPtr)->leftPtr), value);
еlse
if (value > info(*RootPtr))
// если больше – то в правое
insertTree(&((*RootPtr)->rightPtr), value);
else
// при вводе повторяющегося элемента
// выводится сообщение
printf("%d дубль", value);
}
Существует три вида обхода дерева:
Симметричный обход.
Прямой обход (сверху вниз).
Обратный обход (снизу вверх).
Отличаются они лишь порядком прохождения дерева.
Симметричный обход осуществляется согласно следующим шагам:
обход левого поддерева;
обработка значения в корне поддерева;
обход правого поддерева.
// Функция, осуществляющая симметричный обход дерева
void inOrder(TreePtr RootPtr)
{
if (RootPtr != NULL) // если дерево существует
{
inOrder(leftS(RootPtr)); // обход левого поддерева
printf(“%d ”, info(RootPtr)); //печать корня
inOrder(rightS(RootPtr)); // обход правого поддерева
}
}
Таким образом, можно увидеть, что значения в корне не будут обрабатываться до тех пор, пока не будут обработаны его значения в левом поддереве. То есть сначала выводится значение левого потомка, потом значение корневого элемента данного поддерева, а потом значение правого потомка.
На рис. 9.12 приведен результат симметричного обхода дерева, изображенного на рис. 9.11, кружочками обведены значения, которые выводятся на печать
Рис. 9.12. Симметричный обход дерева
Прямой обход осуществляется согласно следующим шагам:
обработка значения в корне поддерева;
обход левого поддерева;
обход правого поддерева.
// Функция, осуществляющая прямой обход дерева
void preOrder(TreePtr RootPtr)
{
if (RootPtr != NULL) // если дерево существует
{
printf(“%d ”, info(RootPtr)); // печать корня
preOrder(leftS(RootPtr)); // рекурсивный вызов для
// обхода левого поддерева
preOrder(rightS(RootPtr)); // обход правого поддерева
}
}
Значение в каждом корне обрабатывается, когда обход дерева проходит через этот узел, после чего обрабатывается значения в левом, а потом в правом поддеревьях. То есть печатается значение корня, затем значение корня левого поддерева, а потом правого.
На рис. 9.13 приведен результат прямого обхода дерева, приведенного на рис. 9.11.
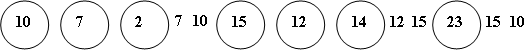
Рис. 9.13. Прямой обход дерева
Обратный обход осуществляется по правилу:
обход левого поддерева;
обход правого поддерева;
обработка значения в корне поддерева.
// Функция, осуществляющая обратный обход дерева
void postOrder(TreePtr RootPtr)
{
if (RootPtr != NULL) // если дерево существует
{
postOrder(leftS(RootPtr)); // с помощью рекурсивного
// вызова функции обходится
// левое поддерево
postOrder(rightS(RootPtr)); // -- правое поддерево
printf(“%d”, info(RootPtr)); // вывод на печать значения
} // корня поддерева
}
Значение в корне поддерева не обрабатывается до тех пор, пока не обработаны узлы-потомки в его поддеревьях. То есть, сначала выводится значения корня левого поддерева, затем значение корня правого поддерева, а потом значение самого корня. На рис. 9.14 приведен результат обратного обхода дерева, изображенного на рис. 9.11.
Рис. 9.14. Обратный обход дерева
Удаление элементов из дерева осуществляется по особому правилу.
Для того чтобы удалить узел, сначала его необходимо найти. Так как бинарные деревья двоичного поиска имеют свое правило построения, для поиска используется это же правило. Удаляемый элемент сравнивается с корнем, если они равны, то удаляемый узел найден, если же удаляемый элемент меньше корня, то далее поиск происходит в левом поддереве корня, если больше – то в правом.
Когда удаляемый узел найден, надо рассмотреть три случая:
Удаляемый узел является листом.
Удаляемый узел имеет одного потомка или левого или правого.
Удаляемый узел имеет двух потомков.
В первом случае значение указателя на данный узел присваивается некоторому рабочему указателю, а самому указателю на узел присваивается значение NULL. После чего память, на которую указывает рабочий указатель, освобождается.
Во втором случае, если удаляемый узел имеет одного из потомков: правого или левого, при удалении узла, потомок занимает его место в дереве, т.е. указатель в его родительском узле устанавливается на этот узел-потомок.
В третьем случае, когда удаляется узел с двумя потомками, его необходимо заменить одним из узлов его поддеревьев. Замещающий узел – это узел с наибольшим значением в поддереве, но меньше значения в удаляемом узле (т.е. наибольший узел в левом поддереве удаляемого узла) или это узел с наименьшим значением в поддереве, больше значения удаляемого узла (т.е. наименьший узел в правом поддереве удаляемого узла).
В представленной ниже функции удаления замещающим узлом является наибольший узел левого поддерева удаляемого корня.
Этот узел находится путем обхода левого поддерева удаляемого узла справа до тех пор, пока указатель на правый узел-потомок не окажется нулевым. Тут тоже следует рассматривать два случая: замещающий узел окажется либо листом, либо будет иметь левого потомка. Если замещающий узел является листом, то он занимает место удаляемого узла, а соответствующему на него указателю родительского узла устанавливается в значение NULL. Если у замещающего узла есть левый узел-потомок, то после того, как он займет место удаляемого узла, его узел-потомок занимает его место, путем установления указателя в родительском узле замещающего узла на левый узел-потомок замещающего узла.
Ниже приведены две функции, предназначенные для удаления узла из дерева. Функция del является вспомогательной, она используется в случае, когда удаляемый узел имеет потомков.
// Функция удаления
void delNode(int x, TreePtr *rootPtr)
{
TreePtr workPtr;
TreePtr previousPtr = NULL;
if ((*rootPtr) == NULL)
printf("Удаляемого элемента в дереве нет\n");
else
if (x < info(*rootPtr))
// если элемент меньше корня - поиск в левом поддереве
delNode(x, &((*rootPtr)->leftPtr));
else
if (x > info(*rootPtr))
// если больше корня - поиск в правом поддереве
delNode(x, &((*rootPtr)->rightPtr));
else
{
// рабочему указателю присваивается значение
// указателя на найденный узел
workPtr = *rootPtr;
if ((rightS(workPtr) == NULL)
&& (leftS(workPtr) == NULL))
// если найденный узел – лист, указатель обнуляется
*rootPtr = NULL;
else
if (rightS(workPtr) == NULL)
// если есть левый потомок, указателю
// родительского узла присваивается значение
// указателя на левый потомок
(*rootPtr) = leftS(workPtr);
else
if (leftS(workPtr) == NULL)
// если есть правый потомок, указателю
// родительского узла присваивается значение
// указателя на правый потомок
(*rootPtr) = rightS(workPtr);
else
del(leftS(workPtr), previousPtr, &(*rootPtr));
delete(workPtr); //удаляется узел
}
}
// вспомогательная функция для удаления узла
// с двумя потомками
void del(TreePtr workPtr,
TreePtr previousPtr,
TreePtr *rootPtr)
{
TreePtr ptr = workPtr;
// поиск наибольшего узла в левом поддереве удаляемого узла
if (rightS(workPtr) != NULL)
{
previousPtr = workPtr; // сохраняется значение
// предыдущего указателя
del(rightS(workPtr), previousPtr, &(*rootPtr));
}
else // если замещающий узел найден
{
// указателю родительского узла замещающего корня
// присваивается значение указателя на левое поддерево
previousPtr->rightPtr = leftS(Ptr);
//замещающий узел перемещается на место удаляемого
ptr->rightPtr = rightS(*rootPtr);
ptr->leftPtr = leftS(*rootPtr);
workPtr = *rootPtr;
*rootPtr = ptr;
}
}
Прошивка.
Поскольку бинарное дерево с n узлами имеет n+1 нулевых указателей, половина выделенной для указателей памяти тратится впустую. Эту память можно использовать для повышения эффективности прохождения бинарного дерева, т.е. хранить в пустых указателях адреса узлов-приемников, которые надо посетить при заданном порядке обхода. Такие указатели называются нитями, а процесс проведения таких нитей называется прошивкой.
Бинарное дерево называется симметрично прошитым, если при симметричном обходе каждый левый пустой указатель указывает на своего предшественника, а каждый правый – на преемника.
Структура, описывающая прошиваемое дерево, видоизменится:
struct Tree
{
int root;
unsigned char rSign, lSign;
struct Tree *leftPtr;
struct Tree *rightPtr;
};
rSign и lSign – поля признаков, они равны 0, когда соответственно правый и левый указатели пустые; 1 – когда указатели ссылаются соответственно на правое и левое поддеревья; 2 – когда указатели являются нитями.
// Функция симметричной прошивки бинарного дерева
void symmetricThreading(struct Tree **h)
{
if (*h)
{
// Если левый указатель не является нитью
if ((*h)->lSign != 2)
symmetricThreading(&(*h)->leftPtr);
// Если правый указатель не является нитью
if ((*h)->rSign != 2)
symmetricThreading(&(*h)->rightPtr);
// Если левый указатель является пустым
if (!((*h)->leftPtr))
{
(*h)->lSign = 2;
leftThreading(h); // делаем его нитью
}
// Если правый указатель является пустым
if (!((*h)->rightPtr))
{
(*h)->rSign = 2;
rightThreading(h); // делаем его нитью
}
}
}
// Функция установки указателя-нити на предшественника
void leftThreading(struct Tree **h)
{
struct Tree *p = NULL;
for (p = *h; (p != head) && isLeft(p); p = father(p));
(*h)->leftPtr = father(p);
}
// Функция установки указателя-нити на преемника
void rightThreading(struct Tree **h)
{
struct Tree *p = NULL;
for (p = *h; (p != head) && isRight(p); p = father(p));
(*h)->rightPtr = father(p);
}