Заключение

Итак, книга подходит к концу. Я надеюсь, что читая ее вы не слишком скучали. Приношу свои извинения тем, кто счел мои объяснения излишне скучными и сложными. Горные лыжи - непростой вид спорта и не все здесь можно объяснить на пальцах. Очень хочется верить, что эта книга поможет Вам прогрессировать быстрее. Если Вы в чем-то со мной не согласны, надеюсь, что, по крайней мере, я дал вам пищу для размышлений и экспериментов со своей техникой.

В заключение хотелось бы поблагодарить всех, кто последние 25 лет катался рядом со мной, тех, кто учил меня, тех, кого учил я, и тех, кто учился вместе со мной.

И еще один совет под занавес:

Каждый раз возвращаясь со склона, обязательно задайте себе вопрос: Чему я научился сегодня? И вы непременно будете прогрессировать.

Наступает время прощаться. До встречи на склонах.

Приложения

Радиус окружности, наилучшим образом описывающей форму бокового выреза, лыжи используется производителями лыж для описания геометрии той или иной модели. Однако, на практике при резаном скольжении лыжи могут поворачивать с радиусом значительно меньшим, чем собственный радиус бокового выреза. Связано это с тем, что закантованная и загруженная лыжа прогибается таким образом, что опорный кант оказывается прижатым к склону по кривой, радиус кривизны которой всегда меньше, чем собственный радиус бокового выреза лыжи. Для того, чтобы оценить, как угол закантовки влияет на радиус поворота, рассмотрим, как прогибается по дуге закантованная лыжа.

Для того, чтобы определить радиус кривизны прогиба закантованной лыжи достаточно рассмотреть условия касания склона для трех точек на боковом вырезе лыжи: А - носок, В - пятка, С - середина лыжи. На рисунке утрированно изображена лыжа - вид спереди и сверху.

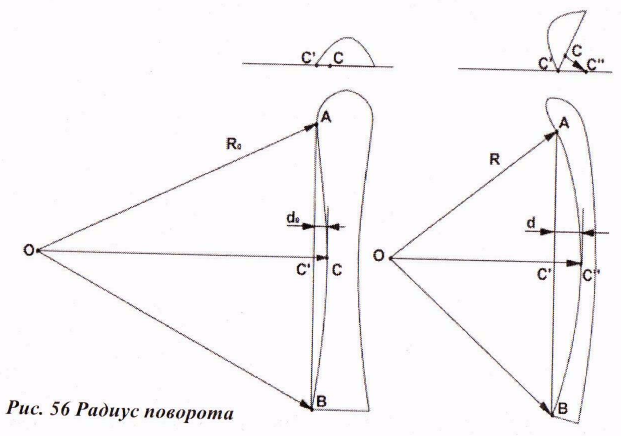
сть Ь - длина канта между точками А и В, а (1₀- глубина бокового

выреза.

Тогда К_₀ - радиус бокового выреза лыжи может быть найден из

соотношения:

а_о(1-Со₈(Ь/2К₀)) = (1₀ (1)

Поскольку для любой нормальной лыжи Ь » (1 .

Соз (Ь/2К₀) ~ 1 - Ь²/8К_Ц² (2) Соответственно, первая формула может быть переписана в виде:

Ь²/⁸**оЧ или

К₀=Ь²Ш₀ (3) Теперь посмотрим, что произойдет, если лыжа будет закантована под углом

а.

В верхней части рисунка изображена лыжа, закантованная под углом ОС, но не прогнутая по дуге. В этом случае лыжа касается склона в точках А и В, а точка С висит в воздухе. Теперь прикладываем к лыже усилие, необходимое для того, чтобы прогнуть ее по дуге, сохраняя заданный угол закантовки. Лыжа будет прогибаться, пока не коснется склона в точке С". Рассмотрим образовавшийся прямоугольный треугольник С"СС'. Собственно, нас интересует его гипотенуза С"С'

С"С' =ё₀ / Соз(ОС) (4)

Рассмотрим, как выглядит ситуация с закантованной лыжей Рис.56 (правая часть).

Как видно из рисунка, картина полностью эквивалентна рассматривавшейся выше, с той только разницей, что в формуле (3) вместо глубины бокового выреза д₀ должна стоять глубина прогиба закантованной лыжи д = ё₀/

Соз(а).

Соответственно, радиус дуги прорезаемой кантом прогнувшейся лыжи

будет равен:

К =Ь² Со8(ОС) / 8с!₀ (5) Или принимая во внимание (3):

К=Я₀Со8(а) (6) ' '