1.4Исследование устойчивости и качества линейной системы автоматического управления

Для нормального функционирования САУ необходимо прежде всего обеспечить устойчивость ее движения. Однако устойчивость есть необходимое, но не достаточное условие, которое отвечало бы требованиям, предъявляемым к качеству систем автоматического управления. Задача исследования качества САУ заключается в определении косвенных или прямых показателей качества, таких, например, как время переходного процесса t_n, максимальное перерегулирование σ %, оценка точности работы система и др.

Систему управления можно представить состоящей из объекта управления и управляющего устройства (Рис.  1 .24).

Рис. 1.24. Структурная схема САУ, где y(t) – управляемая величина, g(t) – задающее воздействие, О – объект управления, УУ – управляющее устройство, e(t) = g(t)–y(t) – ошибка системы управления.

На Рис.  1 .25 представлена типичная переходная характеристика h(t), по которой можно определить основные показатели качества:

1. установившуюся ошибку

2. перерегулирование

3. время переходного процесса t_п - время, в течение которого отклонение регулируемой координаты достигает величины, не превосходящей заданного допустимого значения е_доп.

Качество автоматической системы управления можно оценить ошибкой, возникающей при действии типового сигнала. Наиболее часто пользуются сигналом 1(t) – единичным скачком (Рис.  1 .26).

Рис. 1.25. Общий вид переходной характеристики линейной системы.

Рис. 1.26. Единичный ступенчатый сигнал.

Исследование качества заключается в изучении влияния параметра в САУ на саму ошибку (прямой метод) или на некоторую функцию от ошибки (косвенные методы). Обычно при исследовании считают параметры объекта известными и неизменяемыми, а необходимое качество управления достигается за счет изменения параметров управляющего устройства.

Предметом исследования является линейная система. Объект управления и управляющее устройство заданы передаточными функциями. Передаточная функция объекта:

(1.19)

где k₀ – коэффициент передачи объекта; T₁, T₂ – постоянные времени объекта.

В качестве управляющего устройства поочередно используются три типа регуляторов:

• пропорционально–интегральный (ПИ) регулятор, имеющий соответственно передаточную функцию и уравнение

  	,
  	;

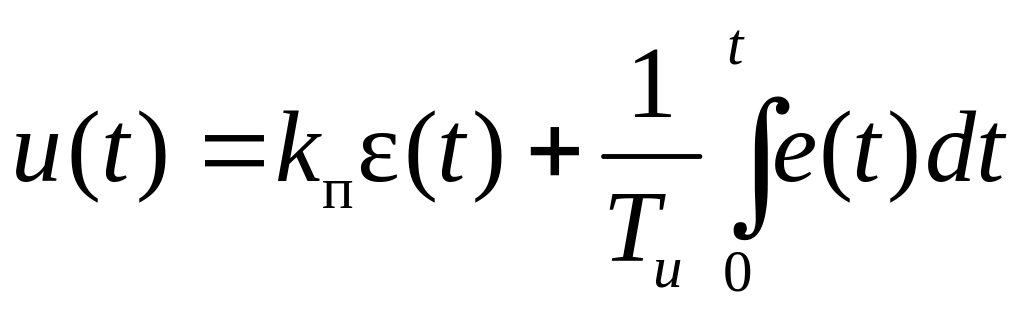• интегральный (И) регулятор

  	,
  	;

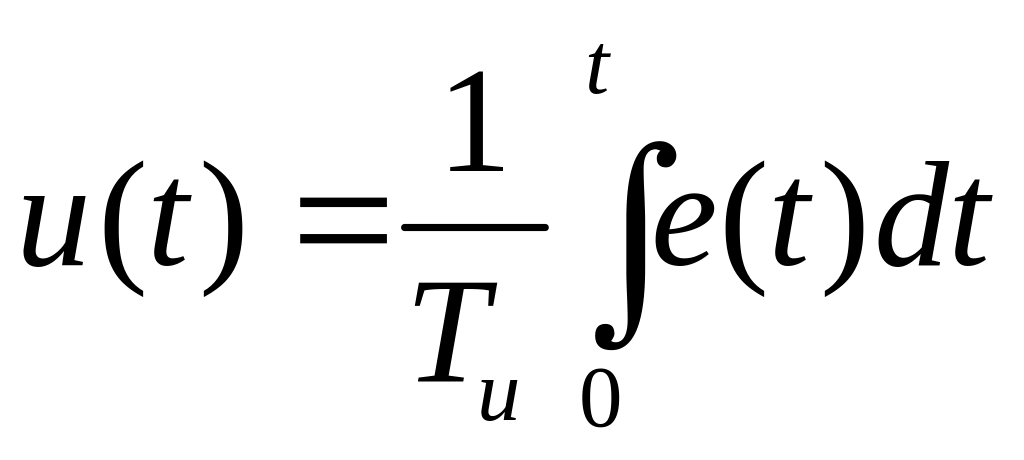• пропорциональный (П) регулятор

	,
	.

Рассмотренные параметры 3-х регуляторов сведены в Таблица 1 .2.

Таблица 1.2

Параметры регуляторов

Наименование регулятора	Обозначение	Алгоритм функционирования	Передаточная функция
Пропорциональный	П
Интегральный	И
Пропорционально– интегральный	ПИ

коэффициент пропорциональности;

постоянная времени интегрирования.