1.2.1.2Дифференцирующее звено первого порядка
Идеальным дифференцирующим звеном первого порядка называется звено, имеющее передаточную функцию вида:
|
|
(1.9) |
,которой соответствует дифференциальное уравнение
|
|
|
.Звено с передаточной функцией ( 1 .9) является физически нереализуемым (m>n). На практике дифференцирующие звенья имеют передаточную функцию:
|
|
|
,которой соответствует дифференциальное уравнение:
|
|
|
Переходная функция реального дифференцирующего звена имеет вид:
|
|
|
График переходной характеристики приведен на Рис. 1 .6. Способ определения параметра T тот же, что и для апериодического звена.
Рис. 1.6. Переходная характеристика дифференцирующего звена первого порядка
На Рис. 1 .6. видно: касательная к h(t) при t = 0 пересекает ось абсцисс при t = T. Тогда h(t) = e-1 = 0,37.
Постоянная времени дифференцирующего звена первого порядка определяется из эксперимента по осциллограмме. На лабораторном стенде дифференцирующее звено первого порядка реализовано на R, C элементах (Рис. 1 .7.).
Рис. 1.7. Дифференцирующее звено первого порядка на RC-элементах.
Передаточная функция этого звена:
|
|
|
,где T = RC.
Аналогично передаточная функция дифференцирующего звена 1-го порядка, реализованная на RL–элементах (Рис. 1 .8), определяется следующим образом:
|
|
|
,где
.
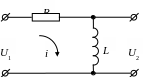
Рис. 1.8. Дифференцирующее звено первого порядка на RL-элементах.
Переходная характеристика, реализованных для звеньев RC и RL (Рис. 1 .7 и Рис. 1 .8), определяется из выражения:
|
|
|
1.2.1.3Колебательное звено
Колебательным звеном называется звено второго порядка, имеющее передаточную функцию
|
|
(1.10) |
Дифференциальное уравнение колебательного звена
|
|
(1.11) |
,где 0≤ξ<1.
Характеристическое уравнение, соответствующее дифференциальному уравнению ( 1 .11) имеет следующий вид:
|
|
|
корни этого уравнения определяются зависимостью
|
|
(1.12) |
.Из выражения ( 1 .12) следует, что при 0 ≤ ξ < 1 корни λ1 и λ2 получаются комплексными, следовательно, для решения уравнения ( 1 .11) будет характерна колебательная составляющая, а при ξ ≥ 1 корни λ1 и λ2 – действительные отрицательные и собственное решение уравнения ( 1 .11) будет иметь затухающий апериодический характер.
Определим переходную функцию колебательного звена. Согласно ( 1 .6) имеем:
|
|
|
,
где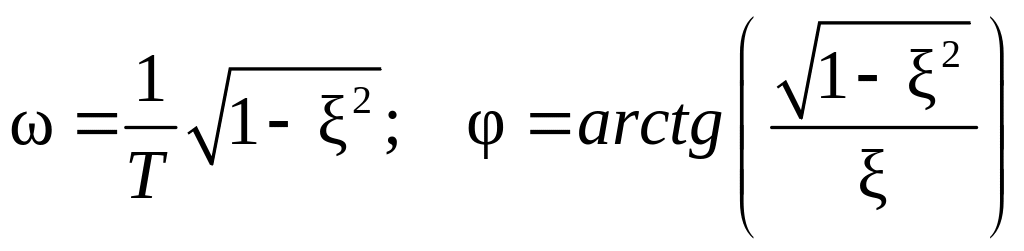 
Переходная характеристика колебательного звена показана на Рис. 1 .9.
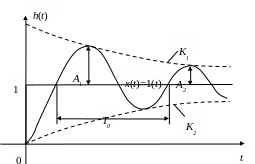
Рис. 1.9.
Переходная характеристика колебательного
звена:
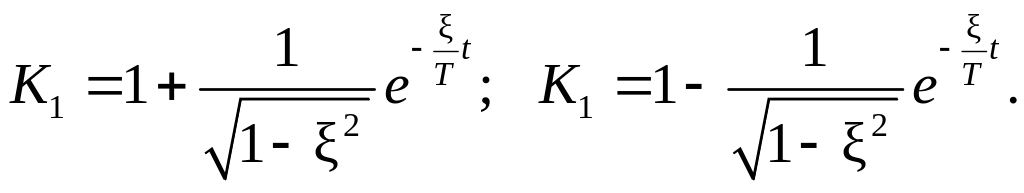
Для переходной характеристики колебательного звена параметры Т и вычисляют по формулам (Рис. 1 .9.):
|
|
|
;
|
|
|
Рассмотрим случай ξ ≥ 1. Передаточная функция Error: Reference source not found может быть представлена как
|
|
(1.13) |
,
где 
;
В частном случае при ξ = 1, T1 = T2.
Звено с передаточной функцией ( 1 .13) (ξ ≥ 1) называется апериодическим звеном второго порядка. Переходная характеристика такого звена имеет вид:
|
|
(1.14) |
График переходной характеристики ( 1 .14) показан на Рис. 1 .10.
Рис. 1.10. Переходная характеристика апериодического звена второго порядка.
Рассмотрим частный случай колебательного звена при ξ = 0.
В этом случае колебательное звено называется консервативным. Его передаточная функция
|
|
|
Переходная характеристика
|
|
|
,представляет незатухающие гармонические колебания с частотой ω0 (Рис. 1 .11).
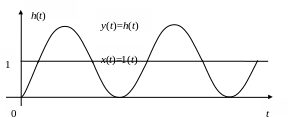
Рис. 1.11. Переходная характеристика консервативного звена.
На лабораторном стенде колебательное звено реализовано на R, L, C‑элементах (Рис. 1 .12).
Рис. 1.12. Колебательное звено на R,L,C–элементах.
Передаточную функцию колебательного звена получим из уравнений:
|
|
|
|
|
|
,
где
;
.
Переходный процесс в цепочке R, L, C (Рис. 1 .12) будет колебательным при выполнении условия
|
|
|
,или
|
|
|
.
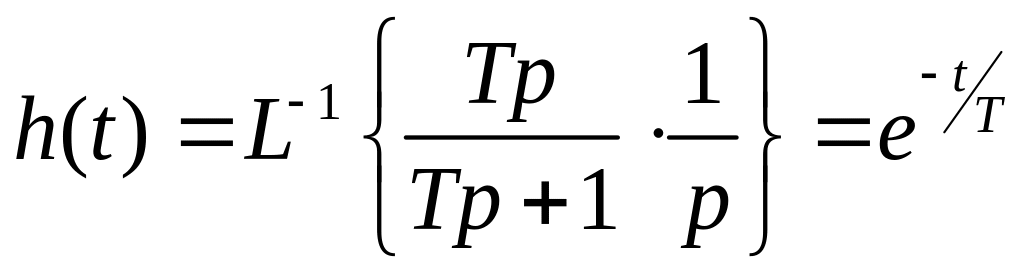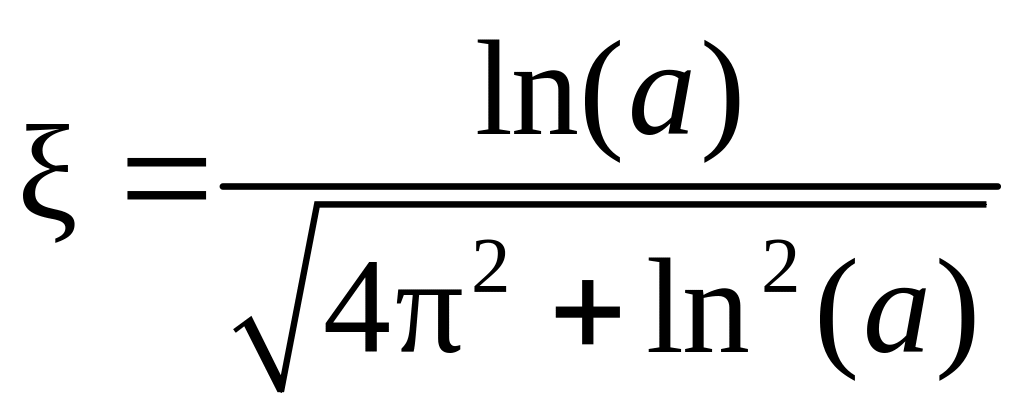
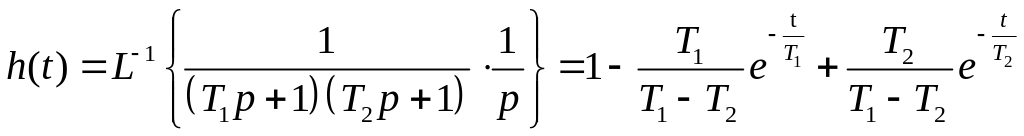
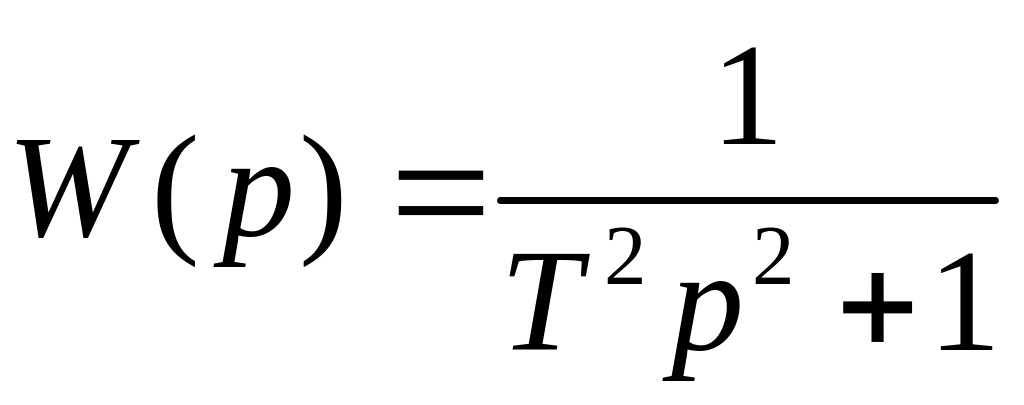
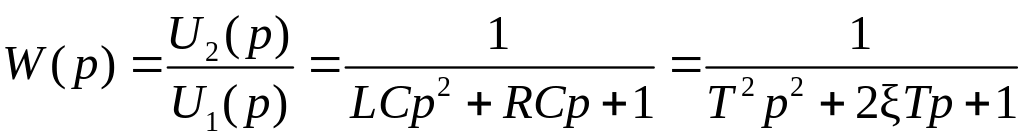