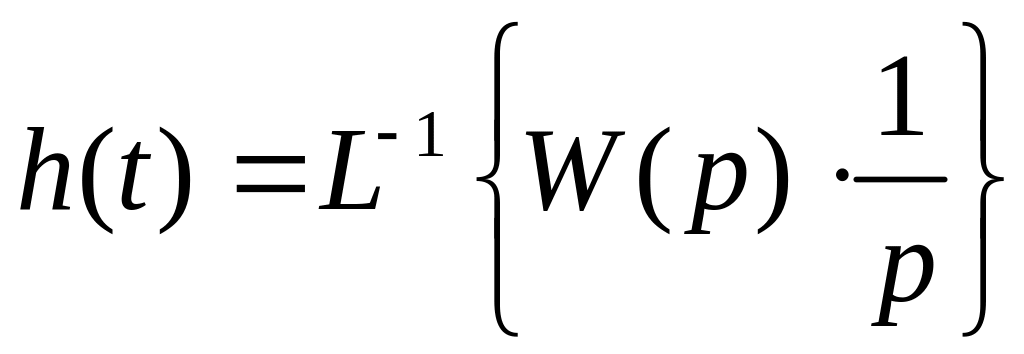Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный исследовательский университет «МИЭТ»

ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО КУРСУ

«ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»

Москва – 2012

СОДЕРЖАНИЕ

1 ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 6

1.1 Общие сведения 6

1.2 Определение параметров типовых динамических звеньев по их временным характеристикам 6

1.2.1 Типовые динамические звенья 8

1.3 Определение параметров типовых динамических звеньев по их частотным характеристикам 18

1.3.1 Апериодическое (инерционное) звено 20

1.3.2 Дифференцирующее звено первого порядка 25

1.3.3 Колебательное звено 27

1.4 Исследование устойчивости и качества линейной системы автоматического управления 31

1.4.1 Определение условий устойчивости системы автоматического управления 34

1.4.2 Анализ точности системы автоматического управления 35

1.4.3 Интегральная оценка качества 38

1.4.4 Выбор оптимальных параметров управляющего устройства по минимуму интегральной оценки 39

2 РАБОТА В СИСТЕМЕ MAtLAB 42

2.1 Рабочее окно программы 42

2.2 Окно текущего каталога 42

2.3 Окно рабочей области 42

2.4 Окно предыстории 43

2.5 Командное окно 43

2.6 Программирование в системе MatLab 43

2.6.1 Создание M-файлов 44

2.6.2 Вывод графиков 46

2.7 Моделирование в среде Simulink 49

2.7.1 Запуск среды 49

2.7.2 Создание моделей 50

2.7.3 Построение основных частотных и временных характеристик линейной системы управления 55

2.8 Создание исполняемого файла 58

2.8.1 Назначение компилятора MatLab 58

2.8.2 Конфигурирование компилятора 59

2.8.3 Среда разработки Deployment Tool 61

2.8.4 Создание приложения 62

2.8.5 Использование команды mcc 67

3 ЗАДАНИЕ 68

3.1 Определение параметров типовых динамических звеньев по их временным характеристикам 68

3.1.1 Порядок выполнения работы в системе MatLab 68

3.1.2 Моделирование с использованием GUI-приложения 73

3.1.3 Лабораторное задание 74

3.1.4 Содержание отчета 75

3.1.5 Контрольные вопросы 76

3.2 Определение параметров типовых динамических звеньев по их частотным характеристикам 77

3.2.1 Порядок выполнения работы в системе MatLab 77

3.2.2 Моделирование с использованием GUI-приложения 83

3.2.3 Лабораторное задание 84

3.2.4 Содержание отчета 86

3.2.5 Контрольные вопросы 86

3.3 Исследование устойчивости и качества линейной системы автоматического управления 87

3.3.1 Порядок выполнения работы в системе MatLab 88

3.3.2 Моделирование с использованием GUI-приложения 96

3.3.3 Лабораторное задание 97

3.3.4 Содержание отчета 98

3.3.5 Контрольные вопросы 98

СПИСОК ЛИТЕРАТУРЫ 100

ПРИЛОЖЕНИЕ 1 101

ПРИЛОЖЕНИЕ 2 104

ПРИЛОЖЕНИЕ 3 108

1Теория автоматического управления

1.1Общие сведения

1.2Определение параметров типовых динамических звеньев по их временным характеристикам

При математическом анализе систем автоматического управления, в первую очередь представляет интерес тип дифференциального уравнения и его коэффициенты, а не принцип действия или конструкция данного элемента.

Любая сложная система автоматического управления (САУ) состоит из простых устройств звеньев (Рис.  1 .1), элементов, которые, как и всю САУ, можно представить в виде математических моделей, то есть дифференциальными уравнениями, связывающими выходные сигналы с входными.

Рис. 1.1. Отображение толщины штриха линейных кодов с разной плотностью на рабочей поверхности матрицы фоточувствительных элементов

,

(1.1)

где y(t) ‑ сигнал на выходе звена;

x(t) ‑ сигнал на входе звена.

Для физически реализуемых систем всегда m ≤ n.

В дальнейшем будем считать, что x(t) ≡ 0 при t< 0, а начальные условия в системе нулевые, т.е.

В операторной форме уравнение ( 1 .1) можно привести к виду:

,

(1.2)

где ‑ оператор дифференцирования.

Если полиномы в скобках обозначить через , то дифференциальное уравнение ( 1 .2) можно записать более компактно:

(1.3)

Если преобразовать временные переменные по Лапласу, то уравнение ( 1 .3) можно записать в преобразованном виде:

(1.4)

где X(p) и Y(p) ‑ изображения Лапласа от x(t) и y(t);

p ‑ комплексная переменная.

Из уравнения ( 1 .4) имеем:

(1.5)

Выражение ( 1 .5) позволяет определить изображение Y(р) сигнала на выходе системы по изображению X(p) входного сигнала, умноженному на некоторый оператор W(p), называемый передаточной функцией. Таким образом, передаточная функция представляет собой отношение изображения Лапласа выходного сигнала к изображению Лапласа входного сигнала при нулевых начальных условиях:

Передаточная функция и дифференциальное уравнение являются равнозначными характеристиками динамического звена. Сигнал y(t) определяется либо из решения дифференциального уравнения ( 1 .1), либо из выражения ( 1 .5):

На практике наибольший интерес представляет реакция звена на один из типовых сигналов.

Для расчетов САУ широкое применение получила так называемая переходная характеристика, представляющая собой реакцию системы на единичный ступенчатый сигнал 1(t) (Рис.  1 .2) и обозначаемая h(t):

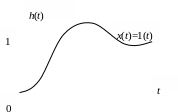
Рис. 1.2. Общий вид переходной характеристики звена

Изображение Лапласа единичного ступенчатого сигнала:

Тогда

(1.6)