Закони розподілу дискретної випадкової величини X

1. Біноміальний розподіл ДВВ X – числа появи події в n незалежних випробуваннях, в кожному з яких імовірність появи події дорівнює p, а ймовірність можливого значення X = k (числа k появи події в n незалежних випробуваннях) обчислюють за формулою Бернуллі. За умови, коли число випробувань n велике (n  100), а ймовірність появи події p в кожному випробуванні дуже мала (p0; 0  np  10) то користуються наближеною формулою P_n(k) = ( ) / k! , де  – середнє число появи події в n випробуваннях (= np = const).

2. Розподіл Пуассона визначає імовірність появи k подій за проміжок часу t, тобто є математичною моделлю найпростішого потоку подій. Потік подій – послідовність подій, які наступають у випадкові моменти часу. Пуассонівський потік має такі три властивості: 1) стаціонарність – імовірність появи k подій за проміжок часу t є функція, яка залежить тільки від k і t, але не залежить від початку відліку часу; 2) відсутність післядії – імовірність появи k-ої події за будь-який проміжок часу t не залежить від того, з’являлися або не з’являлися події в моменти часу, які передували початку даного проміжку (передісторія потоку не впливає на ймовірність появи подій в найближчим майбутнім); 3) ординарність – поява двох або більш подій за малий проміжок часу практично неможливий. Імовірність появи k подій простішого потоку за проміжок часу t визначається формулою Пуассона:

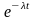P_t(k) = (t)^k  / k! ,

де  – інтенсивність потоку (середнє число подій, які з’являються в одиницю часу).

Закони розподілу неперервної випадкової величини X

1. Рівномірний розподіл – розподіл імовірностей НВВ X, якщо на інтервалі (а, в), якому належать всі можливі значення X, диференціальна функція зберігає постійне значення, а саме

f (x) = = const,

а зовні цього інтервалу, тобто для x  а і для x  в, маємо f (x) = 0.

Інтегральна функція рівномірного розподілу має вигляд:

F(x) = 0, при x  а ; F(x) = (x – a) / (b – a) при а < x  b; F(x) = 1 при x > b.

2. Показниковий (експоненціальний) розподіл – розподіл імовірностей НВВ X, яке описується диференціальною функцією

f (x) =

де  – постійна додатна величина.

Інтегральна функція показникового розподілу має вигляд:

F(x) =

Імовірність попадання в в інтервал (а, в) неперервної випадкової величини X, розподіленої за показниковим законом

P (а  X  в) = .

3. Нормальний розподіл – розподіл імовірностей НВВ X, якщо диференціальна функція має вигляд

f (x) = ,

де а – математичне сподівання; – середнє квадратичне відхилення випадкової величини X. Якщо нормальний розподіл має параметри а = 0 та =1, то маємо нормалізований нормальний розподіл:

f (x) = 1/  exp (– x²/2) .

Імовірність того, що X прийме значення, що належить інтервалу ( ) визначається співвідношенням

P ,

де  (x) = – функція Лапласа.

Імовірність того, що абсолютна величина відхилення менше додатнього числа 0 така

P .

Покладемо / = t, тоді будемо мати

P .

Це означає, що значення подвоєної функції Лапласа при заданому t визначає ймовірність того, що відхилення (X – a) нормально розподіленої випадкової величини X за абсолютною величиною буде менше t . Зокрема, при а = 0 слушна рівність

P .

Наведемо графік нормальної (гауссової) кривої, отриманої автором у праці [10].

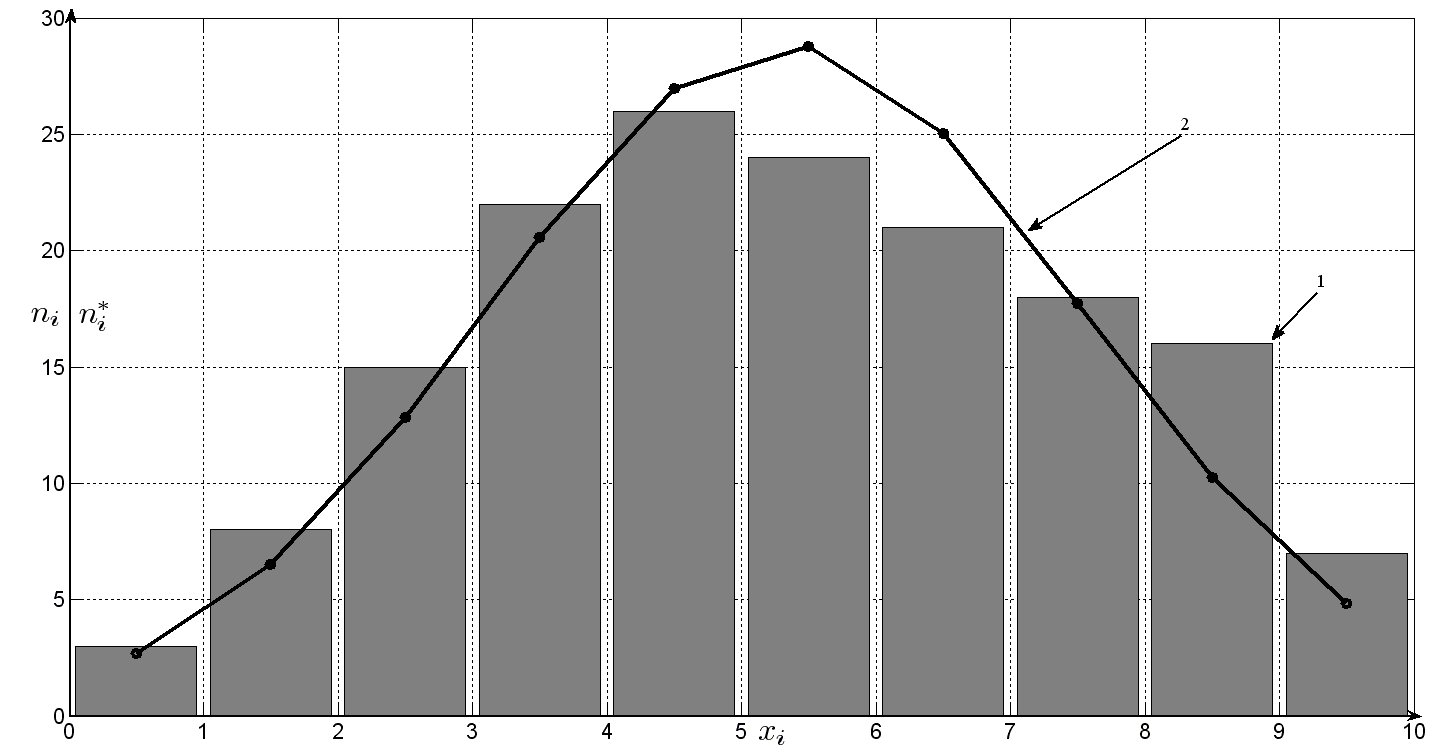
Рис.1. Гістограма (1) і нормальна крива (2), що побудована за (завдання №16)

Числові характеристики випадкових величин (основні параметри теоретичного розподілу).

Нехай x_i ,i – можливі значення ДВВ, p_i – відповідні їм імовірності, тоді характеристикою середнього значення випадкової величини X служить математичне сподівання (генеральна середня):

m  M (X) = .