10.5 Определение оптимальных размеров поперечного сечения пролетной балки

10 5.1. Расчет размеров в средней части пролета из условия обеспечения прочности

Схема расчетного поперечного сечения двоякосимметричной балки с рельсом по оси пояса приведена на рис. 10.3.

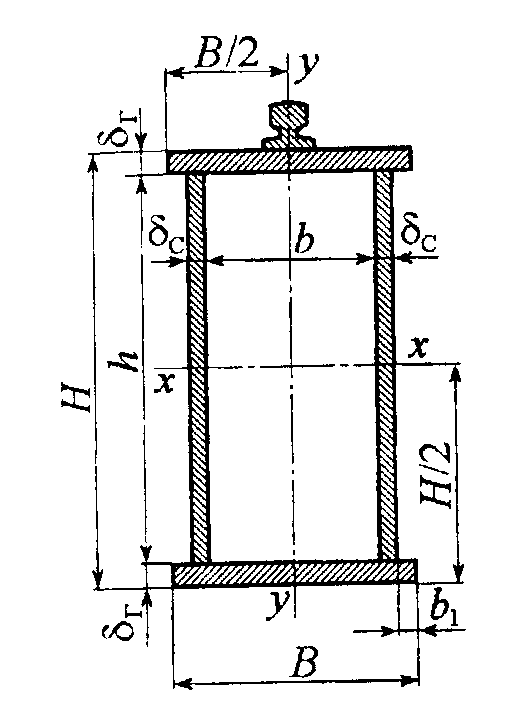Рис. 10.3. Поперечное сечение балки

Расчет проводим по первому предельному состоянию (потеря несущей способности) при дейст­вии нагрузок комбинации II А (см. табл. 3.1).

Необходимая величина мо­мента сопротивления балки при изгибе в вертикальной плоскости

где — коэффициент не­полноты расчета. γ₁=0,90; γ₂=0,95; γ₃=0,90 (см. табл. 5.1, 5.2 и 5.3).

Подставляя в формулу численные значения параметров и коэффициентов, имеем

м³.

Оптимальная по условию минимума веса толщина стенки балки (если принять ) при обеспечении ее прочности

где Н— высота стенки.

Это равенство не позволяет однозначно определить тол­щину стенки, так как в нем неизвестны Н и δ_С. Реальная высота балки у существующих мостовых кранов колеблется в делах 1,0... 1,8м. Определим толщину стенки при различной ее высоте по формуле (10.1) для Н_С1=1,0м, Н_С2=1,2м, Н_С3=1,4 м, Н_С4=1,6м, Н_С5=1,8 м. Результаты расчета введем в табл.10.1.

10.5.2. Расчет размеров в средней части пролета из условия обеспечения статической жесткости

Минимальный момент инерции балки при обеспечении нормальной величины статического прогиба моста (см. табл. 5.6 и формулу (5.8)) при нормативных подвижных нагрузках

м⁴.

Здесь - относительный статический прогиб моста; м; кН 1 нормативная подвижная нагрузка; МПа — модуль упругости материала.

Толщина стенки

где — высота балки.

Придавая высоте балки различные значения, получим соответствующие величины толщины стенки. Результаты, как и в предыдущем случае, введем в табл. 10.1.

10.5.3. Определение размеров поперечного сечения пролетной балки

Для наглядности и удобства пользования данными табл. 10.1 построим графики зависимости высоты стенки балки от ее толщины - рис. 10.4, из которых видно, что определяющим является условие обеспечения жесткости конструкции, а не ее прочности. Так, например, при высоте стенки 1,4м ее оптимальная толщина по условию прочности составляет лишь 7 мм, а по условию жесткости 13 мм.

Таблица 10.1

Толщина стенки при различной ее высоте

Толщина стенки	Высота стенки, м
	1,0	1,2	1,4	1,6	1,8
По условию прочности ,м	0,011	0,0076	0,0056	0,0043	0,0034
По условию жесткости , м	0,0355	0,0205	0,0129	0,0087	0,0061

Высота балки мостовых кранов обычно составляет 1/16... 1/18 пролета, значит, для проектируемого крана с про­летом L=22,5м H=(1,4...1,25)м.

Примем высоту стенки H =1,4 м и по графику (рис. 10.4) получим оптимальную толщину стенки =0,013 м. Ширину пояса для обеспечения жесткости балки в горизонтальной плоскости рекомендуется принимать и

Тогда м и м. Принимаем В=0,47 м. Толщину пояса определяем по формуле (5.10):

м.

Данное сечение пролетной балки имеет момент инерции

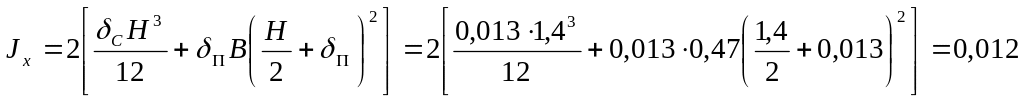м⁴.

Превышение =0,012 м⁴ по отношению к требуемому моменту инерции =0,0059 м⁴ говорит о том, что балка с выбранными параметрами в 2 раза жестче требуемой. Поэтому изменим (уменьшим) толщину стенки до =0,008 м при высоте H =1,3 м. При этом вес балки несколько увеличится. Однако это увеличение несущественно. Так, по данным профессора М. М. Гохберга [13], при отклонении параметров на 20% от оптимального значения вес балки увеличится не более чем на 2,5%. Ширину пояса принимаем В=0,512 м. Тогда его толщина м.

Обычно толщину пояса принимают , в связи с чем м.

Расстояние между стенками м. Полученные расчетные размеры поперечного сечения балки указаны на рис. 10.5.

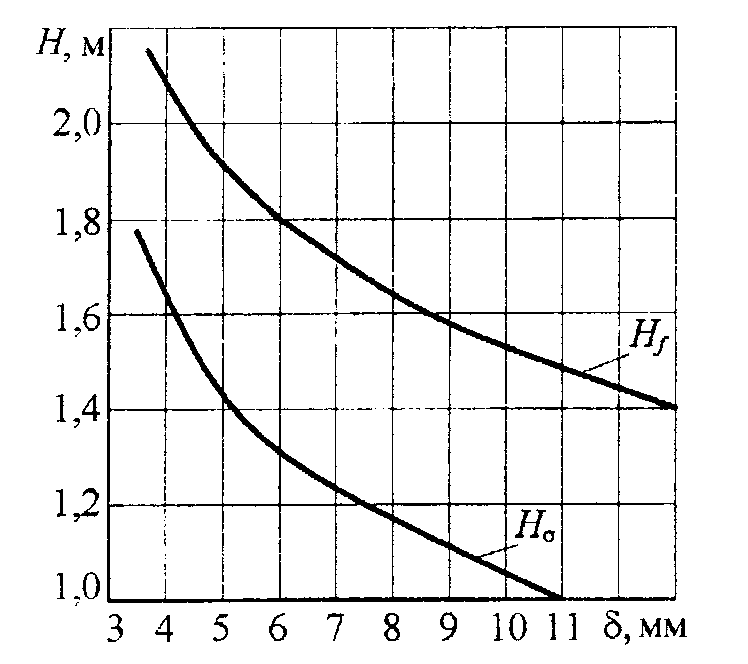
Рис. 10.4 Кривые зависимости высоты балки Н от толщины стенки δ

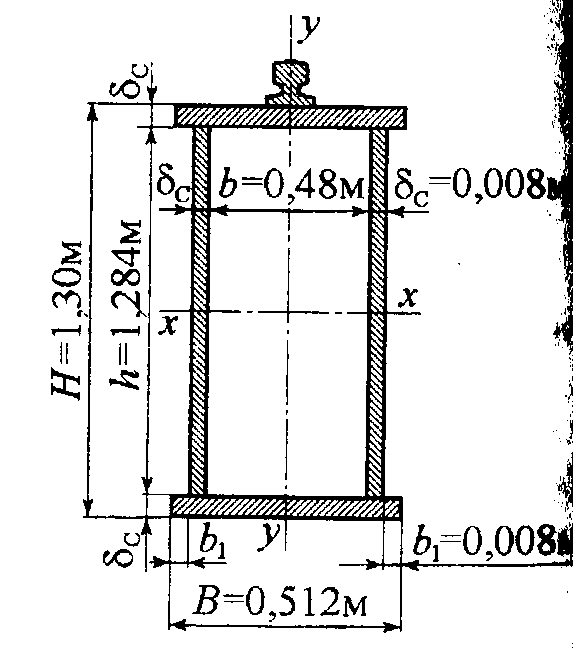
Рис. 10.5. Расчетное сечение балки в середине пролета

Рассчитаем геометрические характеристики данного сечения:

момент инерции в вертикальной плоскости

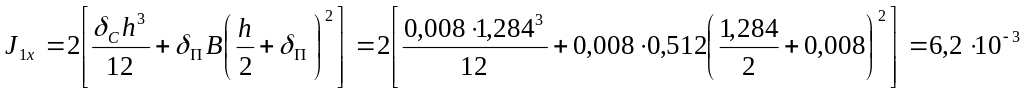м⁴;

момент инерции в горизонтальной плоскости

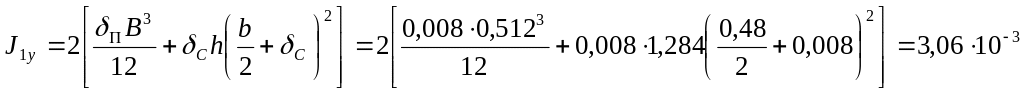м⁴;

момент сопротивления в вертикальной плоскости

м³;

момент сопротивления в горизонтальной плоскости

м³.