
- •Часть 1
- •1. With elem 50
- •2.1. Если поступившая запись предшествует корневой, идти в левое 98
- •2.2. Иначе – в правое поддерево. 98
- •Введение Основные этапы решения задач на эвм
- •Языки программирования
- •Трансляторы
- •1. Общие сведения о языке паскаль
- •1.1. Алфавит языка. Идентификаторы и зарезервированные слова
- •2. Данные в паскале. Простые типы данных
- •2.1. Целочисленный тип
- •2.2. Вещественный тип
- •2.3. Логический тип
- •2.4. Символьный тип
- •2.5. Перечисляемый тип
- •Var m1, m2: metall;
- •2.6. Ограниченный (диапазонный) тип данных
- •Над значениями ограниченного типа допустимы те же операции, что и над значениями базового типа, используемыми при задании в разделе определения типов. Если, к примеру, задано определение:
- •Var y:bukva;
- •3. Операции и выражения
- •2.1. Целочисленный тип
- •3.2. Арифметические выражения и операции
- •3.3. Логические операции и выражения
- •3.4. Операции отношения
- •3.5. Стандартные функции
- •3.6. Приоритеты операций
- •4. Структура программы
- •4.1. Раздел определения констант
- •4.2. Раздел определения типов
- •4.3. Раздел описания переменных
- •V: boolen;
- •4.4. Раздел описания процедур и функций
- •4.5. Раздел операторов
- •4.6. Директивы компилятора и управляющие символы
- •5. Операторы языка паскаль
- •5.1. Оператор присваивания
- •5.2. Оператор вывода информации
- •5.3. Оператор ввода информации
- •5.4. Составной оператор
- •5.5. Условный оператор
- •5.6. Оператор варианта case
- •5.7. Операторы цикла
- •5.7.1. Оператор цикла по счетчику (цикл с параметром )
- •Иденти-фикатор перемен-ной
- •I,n:integer; {I -пар-р цикла, n - его кон.Занч.}
- •X,s,p;integer;
- •5.7.2. Оператор цикла с предусловием
- •Пример составления таблицы переменных
- •Var a,Summa:real;
- •Inc (Summa, a);
- •5.7.3. Оператор цикла с постусловием
- •X,Summa:real;
- •6. Структурированные типы данных
- •6.1. Массивы
- •I,ne:integer;
- •6.1.1. Сортировка массивов
- •Vr:char;
- •Vr : char;
- •6.2. Строки
- •6.3. Множества
- •I : byte;
- •6.4. Записи
- •With elem
- •7. Типизированные константы
- •7.1. Типизированные константы скалярных типов
- •7.2. Типизированные константы - массивы и строки
- •7.3. Типизированные константы – множества
- •Var a: hvor;
- •I, j, k, simp: byte;
- •7.4. Типизированные константы – записи
- •8. Файлы
- •8.1. Типизированные файлы
- •8.2. Текстовые файлы
- •Var f : text;
- •9. Подпрограммы
- •9.1. Процедуры и функции
- •9.2. Процедуры и функции пользователя
- •Var p: real;
- •Var p: real;
- •9.3. Параметры подпрограмм
- •Var X: real; m: integer;
- •Var I : integer;
- •10. Рекурсии
- •10.1. Рекурсивные алгоритмы и определения
- •10.2. Рекурсивные процедуры и функции
- •Var f : longint ;
- •Var a, y, z : real;
- •10.3. Виды рекурсивных процедур
- •If условие
- •If условие
- •If условие then Recur ; then begin
- •Var k : integer;
- •Var c : char;
- •Var c : char;
- •11. Графика в паскале
- •11.1. Основы работы в графическом режиме
- •11.1.1. Аппаратная и программная поддержка графики
- •11.1.2. Запуск графической системы
- •Var Driver, Mode: integer;
- •Init Graph (Driver, Mode, Path);
- •11.1.3. Обработка ошибок
- •11.1.4. Закрытие видеорежима
- •11.2. Система координат дисплея
- •11.3. Экран и окно
- •11.4. Установка цвета, заполнения и палитры
- •11.5. Построение простейших геометрических образов
- •11.6. Работа с текстом OutText (X,y:integer; txt:string) – вывести строку txt с текущего положения указателя.
- •11.7. Вывод числовых значений
- •12. Программные модули
- •12.1. Структура программного модуля
- •Interface –интерфейсные раздел («видимая» часть модуля)
- •Implementation – раздел реализации («черный ящик»)
- •Interface
- •Var X:integer;
- •Implementation
- •Interface
- •X: integer;
- •Implementation
- •12.3. Ссылки на модули
- •Unit hlp _ sr;
- •Xa, ya, xb, yb, xc, yc: integer;
- •13. Динамическая память
- •Var a1: array[1..300,1..300] of integer.
- •13.1. Адресация памяти
- •13.2. Указатели
- •13.2.1. Операции с указателями
- •13.2.2. Нетипизированные указатели
- •X: integer;
- •13.2.3. Типизированные указатели
- •13.3. Создание и уничтожение динамических переменных
- •X: real;
- •13.4. Администратор кучи
- •Heapend содержит адрес конца кучи
- •13.5. Примеры использования указателей
- •Объявление
- •Var Pr:preco;
- •14. Использование указателей для организации связанных динамических структур
- •14.1. Списки
- •14.1.1. Алгоритмы работы со списками
- •14.2. Организация стека в динамической памяти
- •Var p, st :pstack; {st - указатель на вершину стека}
- •I: integer;
- •14.3. Очереди
- •14.4. Деревья
- •14.4.1. Организация деревьев в динамической памяти
- •14.4.2. Построение полного двоичного дерева
- •I,j :I nteger; I - значение инф. Поля очередной
- •Var p,h:pstack;
- •Inc(I); {создаем новый узел – вершину}
- •Inc(j); {переместим указатель t и переход
- •14.4.3. Алгоритмы работы с двоичными упорядоченными деревьями (деревьями поиска)
- •14.4.4. Рекурсивные алгоритмы работы с двоичными деревьями
- •I, X : integer;
- •Литература
- •Часть 1. Язык программирования Паскаль
I,j :I nteger; I - значение инф. Поля очередной
вершины, j - № уровня}
type
pstack=^element; {Опишем запись для стека. Информац.
element=record поля имеют тип ptree - дерева}
m:ptree;
next:pstack
end;
Var p,h:pstack;
procedure putstack(n:ptree);
begin
new(p);
p^.m:=n;
p^.next:=h;
h:=p
end;
procedure getstack(var n:ptree);
begin
p:=h;
n:=p^.m;
h:=p^. next;
dispose (p)
end;
begin
h:=nil; {стек в начале пуст}
j:=0;
i:=0;
new(kor); {0- уровень, -зн.верш. входим в корень!}
t:=kor;
t^.dat:=i;
t^.r:=nil;
t^.l:=nil;
inc(i);
repeat
while j<n
do begin {спуск}
new(v);
v^.dat:=i;
v^.l:=nil;
v^.l:=nil;
v^.r:=nil;
Inc(I); {создаем новый узел – вершину}
if t^.l=nil
then t^.l:=v
else t^.r:=v; {связывает его с левой или
правой ветвью узла предыдущего уровня}
putstack(t); {запомним: пока в стеке!}
t:=v;
{write (t^.dat);}
Inc(j); {переместим указатель t и переход
end; на следующий уровень}
repeat {подъем}
getstack(t);
dec(j) {взять из стека}
until (j=0) or (t^.r=nil); {либо дошли до корня,
либо не заполнена правая ветвь}
until (t=kor) and (t^.r<>nil); {дошли до корня, и правая
end. ветвь не пуста}
14.4.3. Алгоритмы работы с двоичными упорядоченными деревьями (деревьями поиска)
Двоичное дерево упорядочено (является деревом поиска), если в нём все ключи левого поддерева каждого узла меньше, чем ключ узла, а ключи правого поддерева – больше. Ключ – признак, по которому ведётся поиск – значение одного из информационных полей дерева.
П р и м е р. Необходимо создать базу данных «Рейтинг» для хранения сведений о студентах и их успеваемости. При этом программа должна обеспечивать: 1) добавление новых записей, 2) вывод отсортированной по какому-либо признаку информации (например, по алфавиту, по среднему баллу успеваемости), 3) быстрый поиск нужной записи (например, по фамилиям студентов, по номеру группы), 4) удаление записи.
type preit = ^ treit;
treit = record
fam: string [20]; {фамилия};
Ngr: integer; {№ группы};
srb: real {ср. балл}
…
l, r: preit;
end;
Для выполнения указанных задач удобно хранить информацию в виде упорядоченного двоичного дерева. При этом выбор ключа зависит от поставленной задачи. Если необходимо хранить и выводить информацию по алфавиту, а также вставлять элементы, не нарушая алфавитного порядка, то ключом будет поле fam типа string. Если информация дерева была отсортирована по среднему баллу – соответственно ключом будет поле srb типа real и т. д.
Почему в виде двоичного дерева удобнее хранить подобную информацию, чем в виде, например, связанных списков? Рассмотрим п р и м е р. Пусть необходимо построить связанный список, в котром фамилии распределены по алфавиту, при этом на вход данные поступают случайным образом. В этом случае иногда запись будет вставлена в начало списка, иногда – в конец, иногда – в середину. В среднем, до определения положения вставки новой записи придётся просматривать половину списка. Процесс поиска можно было бы ускорить, если бы вместо такого последовательного просмотра можно было сравнить новую запись с записью из середины списка. В результате такого сравнения можно решить, помещать новую запись после средней или до неё. И далее половину списка игнорировать. Этот процесс следует повторять до тех пор, пока не найдём искомую запись (при поиске) или подходящее место (при вставке).
Например, если в списке 64 записи, то такой метод потребует максимум 7 сравнений, а обычный поиск, в среднем, 32 сравнения. В идеальном случае описанную структуру можно представить в виде двоичного дерева.
Таким образом, в упорядоченных массивах можно быстро найти нужную информацию. Динамические списки можно быстро пополнять новыми элементами, используя память из кучи. Двоичные упорядоченные деревья соединяют оба этих качества и позволяют быстро осуществлять двоичный поиск информации.
Пусть записи поступали в следующем порядке: L, E, R, A, W, H, P, а необходимо запомнить их в алфавитном порядке. Для простоты положим, что каждая запись содержит поле-букву, которое и является ключом. Тогда отсортированный список и упорядоченное двоичное дерево будут выглядеть, показано на рис. 14.6 и 14.7.

Рис. 14.6. Отсортированный список
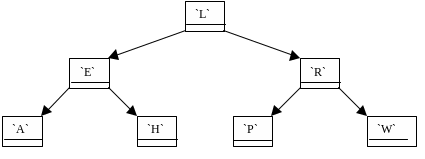
Рис. 14.7. Упорядоченное двоичное дерево
Алгоритм построения двоичного дерева, а также включение новых элементов (процедура bild) будет выглядеть следующим образом:
1. Первая поступившая запись выбирается «корнем» дерева.
2. При поступлении каждая следующая запись сравнивается с корневой.
2.1. Если поступившая запись предшествует корневой, идти в левое
поддерево.
2.2. Иначе – в правое поддерево.
3. Если того поддерева, в которое можно вставить новую запись не существует (на что указывает значение nil левой или правой связи), то новую запись надо вставить в этом месте (тем самым формируя новое поддерево, состоящее из единственной записи).
При этом для вставки новой записи нет необходимости изменять связи, указывающие на другие записи, как для связывания списка.
Алгоритм просмотра входящих в упорядоченное дерево записей и изображения записей, отсортированных по выбранному ключу (prozm (kor)):
Изобразить записи левого поддерева и т. д., пока не будет встречено пустое поддерево, тогда никаких действий не предпринимать.
Изобразить корневую запись.
Напечатать записи правого поддерева, пока не будет встречено пустое поддерево.
Алгоритм двоичного поиска в упорядоченном дереве:
Если дерево не пусто, сравнить искомый ключ с тем, что в корне дерева.
Если ключи совпадают, поиск завершён.
Если ключ в корне больше искомого, выполнить поиск в левом поддереве.
Если ключ в корне меньше искомого, выполнить поиск в правом поддереве.
Если дерево пусто (пройдены все элементы), поиск неудачен.
