14.4. Деревья

Деревья – динамические данные иерархической структуры произвольной конфигурации, состоящие из графов. Граф – это структура, состоящая из узлов (или вершин) и соединяющих их дуг. Графы бывают двух видов: ориентированные и неориентированные (если дуги не имеют стрелок).

Специального вида граф, в котором в каждую вершину может входить только одна стрелка, а выходить несколько, называется деревом (рисю 14.2).

Уровни:

0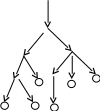

1

2

3

4

а б

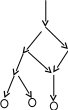
Рис. 14.2. Изображение дерева (а); структура, не являющаяся деревом (б)

Начальная вершина (в которую не входит стрелка) называется корнем. Вершины, из которых не выходят стрелки, – терминальные (листья) (помечены кружками). Структура, выходящая из одного узла – поддерево. Дерево, у которого из каждой вершины выходит не более двух стрелок, называется бинарным или двоичным деревом. Уровень – количество стрелок, которые нужно пройти, чтобы добраться от нулевого уровня к данной вершине.

В дереве может быть только один путь от корня к узлу; дерево не содержит петель и циклов, что следует из определения.

В виде деревьев можно изобразить отношения между субъектами из различных предметных областей.

П р и м е р ы деревьев

Факультет: 5 курсов, на каждом курсе – определенное число групп; в каждой группе – n человек.

Программа на ПК. Ее блоки составляют дерево, дуги которого означают вложенность структур.

Арифметическое выражение можно представить в виде деревьев, в узлах которых находятся операции, за исключением терминальных вершин. В них находятся переменные или числа (рис. 14.3).

Рис. 14.3. Формула в виде двоичного дерева

Для хранения и поиска информации наиболее часто применяют двоичные деревья.

14.4.1. Организация деревьев в динамической памяти

Определить (построить) дерево – значит определить узлы и связи между ними. Применительно к динамической памяти – это элементы комбинированного типа, в которых динамическая переменная может иметь одно и более информационных полей для хранения данных и столько указательных полей, сколько стрелок (максимально) может выходить из вершины.

Для двоичного дерева достаточно двух указательных полей – на левую и правую «ветви»:

Type

ptree = ^ttree ;

tree = record … {информационные поля}

l,r : ptree {указатели на левую

end ; и правую ветвь}

14.4.2. Построение полного двоичного дерева

Дерево называется полным, если все вершины, уровень которых меньше некоторого заданного n, не являются терминальными, а все вершины, кроме терминальных, имеют одинаковое количество выходящих стрелок (рис. 14.4).

Построение полного двоичного дерева состоит из нескольких этапов. Проходя к какой-либо вершине, мы должны запоминать указатель пути. Для этой цели удобно использовать стек. Остановка алгоритма – создание самого правого пути.

П р и м е р. Написать программу построения полного двоичного дерева в динамической памяти из 4-х уровней (рис. 14.4 и 14.5).

1 а б

2

3

4

Р ис. 14.4. Полное бинарное дерево (а) и неполное бинарное дерево из 4-х уровней (б)

Рис. 14.5. Дерево из четырех уровней

{Построение полного двоичного дерева}

const n=4; {сколько уровней}

type ptree=^ttree;

ttree=record {опишем запись для создания дерева}

dat : integer;

l, r : ptree

end;

var

kor,v,t:ptree; {kor -корень, v,t - вспомогательные,