Фаркова Н.А.

ТРЕНИНГ К ИНТЕРНЕТ-ТЕСТИРОВАНИЮ ПО МАТЕМАТИКЕ. МОСКВА . 2009

Теория вероятностей.

1. Основные понятия.

Случайным будем считать всякое событие, которое может либо произойти, либо не произойти в результате некоторого испытания.

Каждому случайному событию ставится в соответствие число , , которое называется вероятностью этого события.

Определения вероятности
Классическое вероятность события равна отношению числа исходов, благоприятствующих наступлению события , к числу всех равновозможных исходов.	Геометрическое вероятности некоторых событий можно вычислить геометрически как отношение длин отрезков, площадей фигур, объемов соответствующих областей.

Аксиоматический подход.

Числовая функция р(А) называется вероятностью события А, если она удовлетворяет следующим аксиомам:

1. Вероятность р(А) есть неотрицательное число, заключенное между нулем и единицей: 0 < р(А) < 1;

2. Вероятность достоверного события равна единице;

3. Вероятность невозможного события равна нулю;

4.Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий р(А + В) = р(А) + р(В).

Тройка ( , F, Р), где — множество элементарных событий, F — допустимое множество составных событий (множество подмножеств ), Р — множество вероятностей случайных событий, называется вероятностным пространством, понятие которое введено А. Н. Колмогоровым. Построение вероят­ностного пространства является основным этапом в создании математической модели того или иного эксперимента.

Алгебра событий. Правила действий над событиями.

Объединением (суммой) событий называется событие , состоящее в наступлении хотя бы одного из этих событий. Обозначается одним из следующих способов:

Пример. В урне 6 шаров, которые отличаются лишь номером. Событие — наугад выбрать шар под номером i. Событие : состоит в том, что будет выбран шар с номером 1 или 3, или 5, т. е. с нечетным номером.

Пересечением (произведением) событий называется событие B, состоящее в обязательном наступлении всех этих событий. Обозначается пересечение событий так:

Пример. В урне 12 шаров, среди которых одна половина белых с номерами от 1 до 6, а другая черных — с такими же номерами.

Пусть — «вынуть белый шар», — «вынуть шар с нечетным номером». Тогда событие означает «выбрать белый шар с нечетным номером».

Как следует из определения, пересечение событий не изменится, если поменять местами сомножители:

Разностью событий и (обозначается - или ) называется событие, заключающееся в наступлении события при одно­временном ненаступлении события .Для предыдущего примера событие означает «выбрать белый шар с четным номером».

Дополнение (противоположное к ) — это событие , состоящее в ненаступлении события . Так, если — «вынуть белый шар», то - вынуть небелый шар».

Пример. При бросании кости вероятность выпадения «6» равна 1/6, а вероятность

противоположного события – невыпадения «6» равна 5/6 .

Достоверным можно считать событие , состоящее из всех элементарных событий, т. е.:

Невозможным же событием можно считать пустое событие , т. е. событие противоположное по отношению к достоверному:

.

События называются несовместными, если в результате одного опыта никакие два из них не могут произойти одновременно. Содержательно это означает, что среди событий нельзя найти такую пару событий и , в которой обнаружилось бы хотя бы по одному общему элементарному событию. Формально несовместность событий и ,, опре­деляется следующим образом:

,.

Например, при однократном бросании игральной кости выпа­дение четного и нечетного числа — несовместные события. Не­совместными являются также промах и попадание при стрельбе по мишени.

Если события и несовместимы, то вероятность суммы этих событий + = равна

Пример. Если событие состоит в выпадении герба, а событие в выпадении решки на одной и той же монете, что эти события несовместимы: в результате испытания может произойти лишь одно из них. Если же событие состоит в выпадении герба на одной монете, а событие в выпадении решки на другой, то эти события совместимы: в результате испытания они могут произойти одновременно.

Говорят, что событие зависит от события , если веро­ятность события В принимает разные значения в зависимости от того, произошло событие или не произошло.

Пример. Предположим, что при подготовке к экзамену две студентки успели выучить только первые пять билетов из два­дцати. Пусть событие - "первая студентка вытянула один из этих (счастливых для неё билетов)", а событие - "вторая студентка вытянула счастливый билет". Если событие произошло, то среди оставшихся 19 билетов окажется только 4 счастливых, и значит, вероятность события В будет равна

Если же событие не произошло, то число счастливых биле­тов среди оставшихся 19 не изменится, и значит, вероятность события будет другой:

Тем самым событие зависит от события .

Произведением событий и В назовем событие, состоящее в совместном наступлении этих событий ( обозначение А • В = А В )

Если события А и В независимы (наступление одного из них никак не влияет на шансы наступления другого), то вероят­ность произведения этих событий равна произведению их вероятностей:

Формула применима для трёх и большего числа испыта­ний. В частности, пользуясь этой формулой, легко вычислить вероятность выпадения герба

при каждом из трёх бросаний мо­неты -

и при каждом из четырех –

Пример. В урне 10 шаров, 3 из которых чёрные, а осталь­ные белые. Из урны последовательно (один за другим) наугад вынимаются два шара. Какова вероятность того, что это будут шары белого цвета?

Искомая вероятность равна

Одновременно мы можем ответить на другие вопросы. На­пример, вероятность того, что шары будут разных цветов, равна

Пример. Имеется 20 экзаменационных билетов, пять из которых - счастливые. У кого больше шансов вытащить счаст­ливый билет - у студента, который берёт билет первым, или у студента, который берёт билет вторым?

Решение. Вероятность того, что первый студент вытащит счастливый билет вычисляется просто - . Вероятность того, что второй студент вытащит счастливый билет равна

,

т.е. шансы равны.

Пример. Студент пришёл на экзамен, зная 25 из 30 билетов. Какова вероятность того, что он сдаст экзамен, если после отказа отвечать на билет ему предоставляется возможность вытянуть ещё один?

Вероятность благоприятного исхода складывается из вероятностей двух несовместимых событий - "студент вытащил счастливый билет с 1-й попытки" и "студент вытащил счастливый билет со 2-й попытки"

Совокупность событий называется полной группой несовместных событий, если: .

События и называются независимыми, если появление одного из них не изменяет шансы появления другого. Например, одновременно бросаются две игральные кости. Появление на одной из них трех очков ни коим образом не зависит от того, какое количество очков появилось на верхней грани другой кости.

Если появление одного события влияет на появление другого, то такие события называются зависимыми.

Пример. В урне 4 пронумерованных подряд и одинаковых на ощупь шара. Вынимается один шар, а затем второй. Событие — первый вынутый шар имеет четный номер. Событие — вынутый второй шар имеет четный номер. Очевидно, что эти события зависимы, т. к. от того, какой шар был вынут в первом опыте, зависят шансы наступления второго события. Действительно, если первым вынули четный шар, то шансы вынуть четный шар и во втором опыте (событие А В) будут вдвое меньше, чем если бы первым был вынут нечетный шар (событие ).

Схема применения классической формулы следующая:

1. Удостоверяются в том, что рассматриваемые условия опыта можно интерпретировать как схему урн (возможные исходы образуют полную группу несовместных равновозможных событий);

2. Выбирается интересующее нас возможное событие (благоприятное событие);

3.Вычисляется число возможных исходов и число благоприятных исходов ;

4. Вычисляется искомая вероятность

Задача. Имеется колода из 36 карт. Наугад вынимаются три карты. Найти вероятность того, что среди них окажется ровно один валет.

Решение. Колода карт относится к одному из наиболее известных примеров схемы урн. В выбранных трех картах может быть три валета, два, один или ни одного валета. Всего в колоде четыре валета. Поэтому реализовать благоприятный случай — выбрать один из них (любой!) можно различными способами, две другие карты (не валеты) можно выбрать различными способами. Следовательно, Общее же число исходов есть число сочетаний из 36 по 4, т. е. . Искомая вероятность вычисляется по формуле:

Пример. Замок имеет четырехзначный цифровой шифр. Наугад выбираются четыре цифры. Какова вероятность открыть при этом замок, если известно, что в коде все цифры различны?

Решение. Поскольку в шифре замка важен не только набор цифр, но и их порядок, то число благоприятных событий равно 1. Общее же число возможных упорядоченных комбинаций из четырех различных цифр определяется по формуле . Таким образом, искомая вероятность:

Геометрические вероятности. Пусть пространство эле­ментарных событий является несчетным, но выполняются следующие условия:

1. Любые два элементарных события несовместны;

2. Все события являются равновозможными.

В таких опытах вероятности некоторых событий можно вычислить геометрически как отношение длин отрезков, площадей фигур, объемов соответствующих областей.

Задача 1. Поезда в метро идут с интервалом в три минуты. Чему равна вероятность того, что пассажир будет ждать поезда более двух минут?

Решение. Считаем, что моменты появления пассажира в интервале между поездами равновероятны. Если все время ожидания принять за интервал длиной три единицы , то событию А — «время ожидания более двух минут», со­ответствует одна единица длины . Следовательно, искомая вероятность равна отношению длин временных интервалов: .

Задача 2. Рассмотрим на плоскости две фигуры, одна из которых це­ликом помещается в другой F Испытание состоит в том, что в фигуру F бросается точка, а событие А - что бро­шенная точка попала в фигуру . Тогда вероятность события А (геометрическая вероятность] определяется как отношение площадей соответствующих фигур

Пример. В результате урагана был оборван телефонный кабель между 20-м и 60-м километрами линии. Вероятность того, что обрыв произошел между 30-м и 50-м километрами определяется равенством .

Основные теоремы.

Изложенные выше прямые методы вычисления вероятностей не всегда эффективны, а иногда и просто невозможны. На практике искомую вероятность часто находят косвенными методами, позволяющими по известным вероятностям одних событий находить вероятности других событий, с ними связанных.

В основе этих косвенных методов лежат основные теоремы теории вероятностей.

Условная вероятность.

Простой пример связи между двумя событиями - причинно-следственная связь, когда наступление одного события ведет к обязательному осуществлению другого, или же наоборот, когда наступление одного события исключает наступление второго.

Пусть и – два события, порожденных одним опытом , причем .

Число, обозначаемое символом , называется вероятностью события при условии, что событие произошло или просто условной вероятностью события .

Теорема умножения вероятностей.

Теорема умножения вероятностей
Для независимых событий = .	Для зависимых событий = =

Пусть рас­сматриваются два события и , для которых известны ве­роятности их появления и . Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого события ,т. е. вычисленную при условии, что первое событие имело место: =

В случае произведения п событий имеем:

Из теоремы умножения следует, что .

Для независимых событий (когда = ) формула имеет упрощенный вид:

= .

т. е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Для вероятности произведения п независимых событий формула приобретает вид:

.

Это равенство можно взять в качестве определения независимых событий, т.е. если

вероятность произведения случайных событий равна произведению их вероятностей , то эти случайные события независимы.

Пример. Механизм собирается из трех одинаковых деталей и считается неработоспособным, если все три детали вышли из строя. В сборочном цехе осталось 15 деталей, из которых 5 не­стандартных (бракованных). Какова вероятность, того, что собранный из взятых наугад оставшихся деталей механизм будет неработоспособным.

Решение. Обозначим искомое событие через А, а выбор первой нестандартной детали через А,, второй — через А2 и третьей — через А3. Событие А произойдет, если произойдет и событие А,, и событие А2, и событие А3. Однако события А1, А2, А3 зависимы и, если вероятность выбрать первую нестандартную деталь равна 5/15, то вероятность выбрать вторую нестандартную деталь равна 4/14, третью нестандартную деталь — 3/13. Следовательно, используя формулу (1.2), имеем:

Пример. Какова вероятность, что взятая наугад кость домино будет «дублем», если сумма очков на этой кости – четное число?

Пусть событие А – взятая кость является « дублем», а событие В – сумма очков четна .

Имеем .

(учтено, что из 28 костей домино 16 с четной суммой, 7 – дубли, и все дубли имеют четную сумму)

Пример. В ящике имеются 7 белых и 5 черных шаров, отличающихся лишь цветом. Опыт состоит в том , что сначала вынимают ( не глядя) один шар, и ,не опуская его обратно, вынимают еще один шар. Вероятность того, что оба вынутые шара будут черными определяется равенством = = .

Теорема сложения вероятностей. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность произведения этих же событий:

= + - .

Пример. Производится два независимых выстрела в одну и ту же мишень. Вероятность попадания при первом выстреле 0.6, а при втором — 0.8. Найти вероятность попадания в мишень при двух выстрелах.

Решение. Обозначим попадание при первом выстреле как событие , при втором — как событие . Попадание в мишень предполагает хотя бы одно попадание: или только при первом выстреле, или только при втором, или и при первом, и при втором. Следовательно, в задаче требуется определить вероятность суммы двух совместных событий и .

Поскольку события независимы, то Поэтому: .

Для вероятности суммы трех событий:

P(А+В+С) = Р(А) + Р(В)-Р(АВ)- Р(А-С)- Р(В-С) + Р(АВС).

При увеличении числа слагаемых формула вероятности суммы все более усложняется. На практике при решении некоторых задач целесообразен переход к противоположному событию. При этом используют известное правило:

Вероятность суммы противоположных событий всегда равна единице, т. е.:

В общем случае

.

Пример. Ремонтное ателье обслуживает пять клиентов. Вероятность вызова на обслуживание от каждого клиента равна 0.2. Какова вероятность того, что в данный момент ателье занято обслуживанием клиентов.

Решение. Очевидно, что событие А «быть занятым обслуживанием клиентов» есть сумма событий , где . — «быть занятым обслуживанием i-ro клиента». Проти­воположное событие «не быть занятым обслуживанием клиентов» определяется как

Следовательно,

.

Полная вероятность и формула Байеса.

Формула полной вероятности. Рассмотрим следующую ситуацию. Приобретается компьютер, который может быть изготовлен с полным комплексом тестирования или по со­кращенному варианту. Известно, какая часть компьютеров изготавливается по сокращенному варианту, а также вероятность безотказной работы компьютера в течение гарантийного срока при различных вариантах изготовления. Какова вероятность того, что приобретенный компьютер безотказно проработает гаран­тийный срок?

Сложность решения данного вопроса обусловлена тем, что неизвестно, какой вариант изготовления реализован при из­готовлении именно приобретенного компьютера. Для решения подобного класса задач наиболее удобно применение формулы полной вероятности, являющейся обобщением теорем умножения и сложения вероятностей.

Сформулируем в общем виде задачу, приводящую к формуле полной вероятности. Пусть некоторое событие А может произойти с какой-то вероятностью только как следствие каждого из событий , образующих полную группу несов­местных событий. Такие события называются гипотезами.

Заданы вероятности гипотез Р( ) и условные вероятности наступления события с каждой из гипотез . Вероятность наступления события дается формулой полной вероятности:

Пример. Имеется три одинаковых урны. В первой два белых и один черный шар, во второй три белых и один черный шар, в третьей урне два белых и два черных шара. Из выбранной наугад урны выбирается один шар. Какова вероятность того, что он окажется белым?

Решение. Гипотезой . будем считать выбор i-ой урны. Все урны считаются одинаковыми, следовательно, вероятность выбрать i-ую урну есть Р( .) = 1/3, i =1,2,3. Зная состав шаров в каждой из урн, легко определить вероятности вынуть белый шар из каждой урны: = 2/3 = 3/4, =1/2. Тогда из формулы имеем: .

Формула Байеса. Рассмотрим ситуацию в некотором смысле противоположную предыдущей. Пусть событие уже произошло, Требуется определить ве­роятность того, что событие произошло именно совместно с гипотезой .Ответ на подобный вопрос дает

Формула Байеса (формула апостериорной вероятности ):

Задача. Пусть сохраняются условия предыдущей задачи, но из урны уже вынут белый шар. Требуется определить вероят­ность, что шар вынут из первой урны.

Решение. Поскольку все вероятности необходимые для применения формулы (1.9) найдены, то имеем:

.

Схема Бернулли и асимптотические формулы.

Эта схема состоит в том, что рассматривается последовательность взаимно независимых испытаний, т. е. таких испытаний, что вероятность того или иного результата в каждом из них не зависит от того, какие результаты насту­пили или наступят в остальных. В каждом из этих испыта­ний может наступить (или не наступить) некоторое событие с вероятностью , не зависящей от номера испытания.

Схема опытов Бернулли. Если проводится одина­ковых и независимых опытов, в каждом из которых событие может произойти с вероятностью , то говорят, что реализуется схема опытов Бернулли.

Пусть — случайное событие, которое может произойти в резуль­тате некоторого испытания. Допустим далее, что нас интересует лишь то, наступило ли событие : будем считать возможными лишь два со­бытия — и . Обозначим их вероятности через и соответственно, .

Предположим, что испы­тание повторяется при одних и тех же условиях некото­рое фиксированное количество раз, скажем, три раза. По­строим дерево вероятностей и вычислим вероят­ности каждого из восьми воз­можных событий:

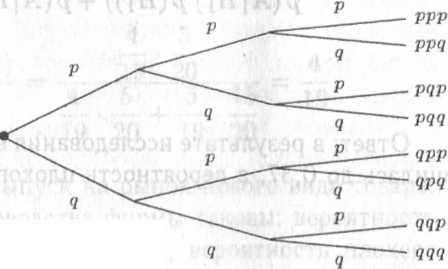
Как мы видим, вероятность каждого из исходов представима в ви­де ,где показывает число наступлений события А, а соответственно число его ненаступлений.

Вероятностные схемы такого рода называются схемами Бернулли, или схемами биномиальных экспериментов. Эти схемы широко при­меняются при анализе реальных ситуаций в тех случаях, когда экс­перимент можно считать биномиальным, т.е. когда

• он состоит из фиксированного числа испытаний,

• в каждом из этих испытаний происходит либо не происходит неко­торое событие,

• вероятность этого события одинакова в каждом испытании,

• испытания независимы одно от другого.

Пример. Тренированный стрелок совершает пять выстрелов по мишени, причем все выстрелы производятся практически в одних и тех же условиях. При этом число попаданий в "десятку" может меняться от 0 до 5.

Пример. В помёте, состоящем из 8 мышей, происходящих от од­них родителей, число мышей, имеющих прямую, а не волнистую шерст­ку может равняться произвольному целому числу от 0 до 8.

Вероятность того, что событие А, которое наступает при одном ис­пытании с вероятностью , произойдет ровно раз после испытаний, обозначим через (ясно, что ).

Справедлива следующая формула Бернулли

Здесь — это вероятность появления события в одном испытании, а число сочетаний называется биномиальным коэффициентом и вычисляется по любой из формул

.

Если положить , то формула принимает вид .

Пример. Монету бросают 10 раз. Какова вероятность того, что при этом "герб" выпадет ровно 3 раза? Выпадет меньше двух раз?

Решение. Здесь ,

Р {"герб" выпал ровно три раза} = .

Р {"герб" выпал меньше двух раз} = Р{"герб" не выпал ни разу} + Р{"герб" выпал ровно один раз} =

Пример. Студент пишет контрольную работу по теории вероятно­стей. У него есть предположение о том, как решить задачу, однако свою способность найти правильное решение студент оценивает невысоко — примерно 0,4.

Вокруг студента в аудитории сидят пять однокурсников. Можно рискнуть опросить их и принять либо отвергнуть решение на осно­вании большинства голосов. Подготовку этих однокурсников студент оценивает так же, как и свою.

Как лучше поступить студенту — положиться на свои соображения или на большинство голосов однокурсников?

Решение. Для выбора между двумя альтернативами следует сначала выбрать какой-либо критерий. По-видимому, в данной ситуации таким критерием является вероятность правильно решить задачу. Опираясь на свои соображения студент получает вероятность 0,4.

Вычислим теперь вероятность того, что большинство из 5 опрошен­ных однокурсников даст правильный ответ. Большинство — это либо 3, либо 4, либо 5. Поэтому искомая вероятность вычисляется следующим образом:

=

= 10 • 0,064 •0,36 + 5 • 0,0256 • 0,6 + 0,01024 = 0,31744.

Вероятность снизилось с 0,4 до 0,31744 — более чем на 20%. Вывод: опрос однокурсников в данной ситуации лучше не проводить.

Если число испытаний велико, то применяют локаль­ную теорему Лапласа

,

где ,

Вероятность появления события от до раз включительно при малых определяется по формуле

,

а при больших определяется с помощью интегральной теоремы Лапласа

где

называется функцией Лапласа,

,

Для вычисления функций и Ф(х) составлены табли­цы, при использовании которых нужно учесть, что функ­ция - четная, т.е. = , а функция Ф(х) -нечетная, т.е. Ф(—х) = — Ф(х).

Пример. Студенту предложено ответить на 100 во­просов. Для данного студента вероятность правильного от­вета на каждый вопрос считается равной 0,8. Какова веро­ятность того, что правильных ответов будет не менее 75.

Решение. По условию = 100, = 0,8, = 75. Поло­жим = 100. Вычисляем

=

Находим по таблицам ,

Формула, выражающая содержание локальной теоремы Лапласа, дает результаты тем более близкие к точному значению , чем больше значение .

При этом здесь сказывается не только число испытаний , но и величина

Таблица значений функции Лапласа содержит ее значения только для положительного аргумента.

Пример. Вероятность появления события при одном опыте равна 0,3. С какой вероятностью можно утверждать, что частота этого события при 100 опытах будет лежать в пределах от 0,2 до 0,4?

Решение. Для того, чтобы частота лежала в пределах от 0,2 до 0,4 в серии из 100 опытов, число появлений события m должно быть не менее 20 и не более 40.

Воспользуемся интегральной теоремой Лапласа

По условию = 100, = 0,3, 1- = 0,7, следовательно,

( таблица )

( таблица )

Формула Пуассона. При одних и тех же значениях вычисле­ние по этой формуле дает тем лучшее приближение, чем ближе к 0,25 (это значение является для наибольшим), т.е. чем заданная вероятность (а отсюда и ) ближе к 0,5. В задачах же со значениями или близкими к 0 локальная теорема Лапласа приводит к заметным отклонениям от точных значений вероятностей , получаемых по формуле Бернулли.

В связи с этим для событий, вероятности наступления которых близки к нулю (их называют редкими событиями), применяется другая приближенная формула - так называ­емая формула Пуассона, которая имеет вид

где - невелико (не превосходит 10). Функция называемая функцией Пуассона, табулирована.

Пример. Из таблицы случайных чисел на удачу вы­писаны 200 двузначных случайных чисел (от 00 до 99). Определить вероятность того, что среди них число 33 встре­тится:

а) три раза; б) четыре раза.

Решение. Вероятность того, что на удачу выбранное дву­значное число равно 33, равна р = 0,01, поскольку выби­рается одно из 100 возможных. Число испытаний = 200. Поскольку число велико, а вероятность р мала, восполь­зуемся формулой Пуассона

где - невелико (не превосходит 10).

a) б)

Пример. Известно, что вероятность изготовления дефектной детали равна 0,004, Найти вероятность того, что среди наудачу взятых 50 деталей нет дефектных.

Решение. Здесь =50 и . Обращаясь к формуле Бернулли, получим, что вероятность искомого события равна

Найдем вероятность того же события по формуле Пуас­сона. В условиях задачи , а . По таблице значений функции Пуассона при и сразу находим , что ,

Т.е. отклонение от точного значения искомой вероятности составляет или .

Итак,

n невелико	формула Бернулли
n велико, а p мало (	формула Пуассона
n велико, а p и q не слишком малы (	формула Муавра-Лапласа

Наивероятнейшее число наступления .

Для практики иногда требуется знать, какое число на­ступлений события является наивероятнейшим, т. е. при каком числе вероятность наибольшая (при этом и предполагаются заданными).

С помощью формулы Бернулли получается во всех слу­чаях найти простое решение поставленного вопроса. Наивероятнейшее значение числа должно удовлетворять двойному неравенству

Промежуток от до , в котором должно лежать число , имеет величину 1, как показывает про­стое вычитание; поэтому если какой-либо из концов этого промежутка не есть целое число, то между этими концами будет обязательно лежать одно и только одно целое число и будет однозначно определено. Этот случай мы должны рассматривать как нормальный: ведь р < 1, и потому лишь в исключительных случаях величина будет це­лым числом. В этом исключительном случае неравенства

дают для числа два значения: и , отличающиеся друг от друга на единицу; эти два значения и будут наивероятнейшими; их вероятности равны между собой и превышают вероятности всех других значений чис­ла .

Пример. В результате многолетних наблюдений для некоторой местности было выяснено, что вероятность того , что в течение 1 июля выпадет дождь равна 4/17. Найти наивероятнейшее число дождливых дней 1 июля за ближайшие 50 лет.

Решение. Здесь =50 и , , число это оказалось целым, значит, мы имеем дело с ис­ключительным случаем, наивероятнейшим значением чис­ла дождливых дней будут равновероятные между собой чис­ла 11 и 12

Пример. В одном физическом эксперименте произ­водятся наблюдения за частицами определённого типа. При одних условиях за промежуток времени определённой дли­ны в среднем появляется 60 частиц и каждая из них с веро­ятностью 0,7 имеет скорость большую, чем . При других условиях за тот же промежуток времени в среднем появля­ется лишь 50 частиц и каждая из них с вероятностью 0,8 имеет скорость большую, чем . Для каких условий опыта вероятнейшее число частиц со скоростью, превосходящей , больше?

Решение. Для первых условий эксперимента =60 и , , = 42.

Для вторых условий эксперимента =50 и , , = 40.

Мы видим, что вероятнейшее число "быстрых" частиц в первых условиях эксперимента несколько больше.

Пример. Что вероятнее

выиграть у равносильного про­тивника: а) три партии из четырех или пять из восьми?

б) не менее трех партий из четырех или не менее пяти партий из восьми?

(Ничейный исход партии исключен).

Решение. Так как противники равносильны, то вероят­ность выигрыша и проигрыша каждой партии одинакова и равна, р = 1 — р = 0,5.

а) Вероятность выиграть три партии из четырех равна . Вероятность выиграть пять партий из восьми равна .

Так как , то вероятнее выиграть три партии из четырех.

б) Вероятность выиграть не менее трех партий из четырех равна

а вероятность выиграть не менее пяти партий из восьми равна

Так как > , то вероятнее выиграть не менее пяти партий из восьми.

Случайные величины

Величина, которая в результате опыта может принимать одно и только одно определенное значение, до опыта неизвестное и зависящее от причин, которые нельзя учесть заранее, называется случайной величиной.

Формальное определение: случайной величиной назы­вается измеримая функция , отображающая про­странство элементарных событий на множество действи­тельных чисел R.

Если множество конечно или счетно, то случайная величина называется дискретной. Примеры дискретной величины: количество уголовных дел, рассматриваемых данным судом за определенное время; количество клиентов; количество диалектов в данном языке; количество избирателей округа, которые примут участие в предстоящих выборах, количество телевизоров, которые необходимо проверить до выявления первого неисправного и т. п.

Итак, дискретной считают такую случайную величину, возможные значения которой можно пронумеровать.

Непрерывной называют такую случайную величину, воз­можные значения которой непрерывно заполняют некоторый промежуток числовой оси, т. е. множество значений имеет мощность континуума. Например, время выхода из строя работающего компьютера, ошибка указателя скорости автомобиля, вес выбранного яблока и т. п.

Понятие о законах распределения случайных величин. Всякое соотношение, устанавливающее связь между возмож­ными значениями случайной величины и соответствующими вероятностями называется законом распределения этой слу­чайной величины. Знание закона распределения позволяет заранее (до опыта!) установить, какое значение случайной величины будет появляться чаще, а какое реже и насколько.

Для дискретной случайной величины законом распределения выступает правило сопоставления каждому возможному значению х. случайной величины X вероятности его появления: . Последнее выражение читается так: «вероятность того, что случайная величина X примет значение х.». Для дискретной случайной величины закон распределения проще всего задавать в виде таблицы

… …

…. ….

Пример. Пусть вероятность прибытия одной англоязычной группы туристов оценивается величиной = 0.6. В случае прибытия шести групп возможно прибытие различного числа таких групп (от 0 до 6). Используя формулу Бернулли

,

можно предсказать вероятность наступления любого из этих исходов. Так, вероятность прибытия двух англоязычных групп равна Р(Х = 2) = 0,138, в два раза меньше, чем прибытие трех таких групп — Р(Х = 3) = 0, 276. Следовательно, формула

есть закон распределения случайной величины : «число англоговорящих туристических групп при ожидаемом прибытии шести, каждая из которых прибывает из неизвестной заранее страны».

Закон распределения для непрерывной случайной величины X есть всякое соотношение, сопоставляющее с каждой измеримой областью ее возможных значений соответ­ствующую вероятность .

Пример. Если среднее время безотказной работы компьютеров данного типа равна s часов, то вероятность проработать без отказа не менее t часов, т. е. Р(Т t), часто может быть выражена законом распределения в форме:

P(T>t) = , при t 0.

Функция распределения. Наиболее универсальной из форм законов распределения является функция распределения.

Функцией распределения F(x) или интегральным законом распределения случайной величины X называется вероятность выполнения неравенства Х< , т. е.:

F(x) = Р(Х<х).

Функция распределения определена для случайных величин любого типа: дискретных и непрерывных.

Определение функции распределения имеет наглядную геометрическую интерпретацию. Если рассмат­ривать X как случайную точку на числовой оси, то F(x) есть вероятность того, что слу­чайная точка попадет левее выбранной величины

Свойства функции распределения непосредственно вытекают из ее определения:

1) F(x) — неотрицательная функция, значения которой заключены между 0 и 1, т. е.:

2) ;

3) ;

4) F(x) — неубывающая функция своего аргумента, т. е., если , то ;

5)

Последняя формула дает прямое решение некоторых практических задач.

Пример. Вероятность попадания при одном выстреле равна 0.4. Производится 4 выстрела. Какова вероятность того, что будет менее двух попаданий?

Решение. Поиск ответа задачи заключается в определении значения функции распределения для значения аргумента х = 2. Действительно, F(2) есть вероятность того, что произойдет менее двух попаданий.

Задача. Время безотказной работы прибора имеет функцию распределения:

Вероятность того, что прибор безотказно проработает не менее 30 и не более 40 часов находится следующим образом:

= .

Функция плотности вероятности. Непрерывную случайную величину удобнее описывать законом распределения, который называют функцией плотности вероятности или диф­ференциальным законом распределения.

Пусть X — непрерывная случайная величина, имеющая функцию распределения . Если эта функция диффе­ренцируема, то можно рассматривать ее производную:

Функция , производная от функции распределения, называется плотностью вероятности случайной величины X или функцией распределения вероятностей.

Из определения плотности вероятности , принимая во внимание, что следует, что

Следовательно, если известна плотность распределения непрерывной случайной величины, то. можно вычислить веро­ятность попадания этой случайной величины в любой заданный промежуток ее возможных значений.

Для задачи предыдущего пункта : ( Время безотказной работы прибора имеет функцию распределения: )

Найдем искомую вероятность через функцию плотности вероятности

.

Основные свойства функции плотности вероятности:

1. Функция плотности вероятности — неотрицательная фун­кция, ;

2. Интеграл в бесконечных пределах от функции плот­ности вероятности (если она задана на всей числовой оси) равен 1.

Как частный случай формулы имеем:

- это равенство называется условием нормировки.

З амечание. Если случайная величина задана только на от­резке , то в последней формуле пределы интегрирования заменяются на и .

Общий вид функции плотности вероятности представлен на рис.. Очевидно, что вероятность попадания в заданный промежуток численно равна площади криволинейной трапеции с основанием .

Числовые характеристики случайных величин

На практике часто затруднительно найти закон распределения. С другой стороны, при решении многих задач достаточно знание лишь основных характеристик случайных величин. К таким характеристикам в первую очередь относятся: математическое ожидание, дисперсия и среднее квадратичное отклонение.

Математическое ожидание. Рассмотрим

Пример. Бросаются одновременно три игральные кости и рассматривания случайная величина — сумма выпавших очков. Вполне очевидно», что выпадение 18 очков будет в среднем происходить реже, чем 15 очков, и значительно реже, чем 12 очков. Если с некоторым «весом» усреднить все возможные значения суммы выпавших очков (от 3 до 18), то получим величину, являющуюся «центром» распределения возможных значений рассматриваемой случайной величины и называемую ее математическим ожиданием.

Для дискретной случайной величины математическое ожидание вычисляется по формуле:

Для непрерывных случайных величин математическое ожида­ние есть величина:

Итак, математическим ожиданием (или средним) называют характеристику положения случайной величины X, которая равна средневзвешенному возможных ее значений. Математическое ожидание есть число (неслучайная величина) — центр группирования значений слу­чайной величины или центр рассеивания.

Пример. Если плотность вероятности времени безотказной работы прибора есть функция , то математическое ожидание, т. е. среднее время безотказной работы, есть величина 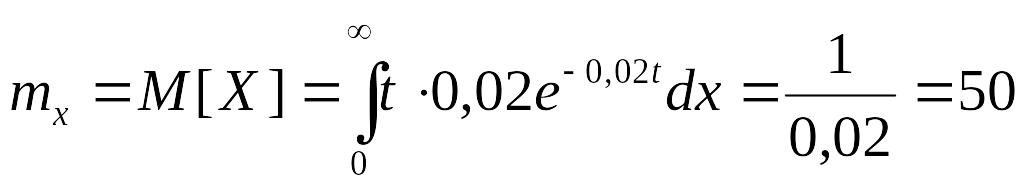(час).

Заметим, что размерность математического ожидания сов­падает с размерностью самой случайной величины.

В задаче о серии из 4 выстрелов с известной вероятностью попадания 0,4 при одном выстреле математическое ожидание равно

Полученное число означает, что, проводя много серий по четыре выстрела в каждой, в среднем будем получать 1.6 попаданий, если вероятность попадания при одном выстреле равна 0.4. В каждой конкретной серии из четырех выстрелов будет ровно или 0, или 1,.., или 4 попадания, но в среднем за много серий их будет 1,6. Этот пример показывает, что математическое ожидание не всегда может быть равно одному из возможных значений случайной величины.

Свойства математического ожидания

1. М [С] = С.

Математическое ожидание постоянной, т. е. неслучайной, вели­чины равно этой постоянной.

Постоянная — вырожденный случай случайной величины, принимающий единственное значение С с вероятностью 1. Тогда М [С] = С 1 = С.

2. М[СХ] = СМ[Х].

Постоянный, т.е. неслучайный, множитель можно вынести за знак математического ожидания.

3. . Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий.

Эти свойства математического ожидания справедливы и для непрерывной случайной величины.

В формуле интеграл несобственный. Он может быть сходящимся и расходящимся. Если он сходится, то дополнительно также требуют, чтобы сходился интеграл . В этом случае математическое ожидание непрерывной случайной величины считается существующим. В противном случае считают, что непрерывная случайная величина не имеет математического ожидания.

В последнем случае как альтернативу математическому ожи­данию для непрерывной случайной величины используют другую числовую характеристику положения так называемую медиану.

Медианой непрерывной случайной величины называется число, обозначаемое символом Me, удовлетворяющее равенству

Р {X <Ме) = Р{Х> Me).

Это равенство можно записать в более удобной форме: Р(Х <Ме) = 1-Р(Х <Ме); 2Р(Х<Ме) = 1; 2F (Me)=l:

F (Me) = 1/2. Если уравнение F (х) = 1/2 однозначно разрешимо относитель­но х, то

формула F (Me) = 1/2. может использоваться для практического отыскания медианы.

Если распределение симметрично, то Me совпадает с центром симметрии.

Если случайная величина Х такова, что ее математическое ожидание равно нулю, то она является центрированной

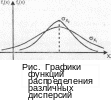Дисперсия. Рассмотрим две случайные величины, плотности вероятности которых представлены на рисунке. Они имеют одинаковое мате­матическое ожидание, однако значительные отклонения от центра рассеивания у первой случайной величины наблюдаются чаще, чем у второй. В этом случае го­ворят, что первая слу­чайная величина имеет большее рассеивание, или размытость, чем вторая.

Другой пример. Рассмотрим два распределения

X	0,01	0,01
	0,5	0,5
Y	100	100
	0,5	0,5

Здесь . Однако характер распределения дискретных случайных величии X и Y существенно различен. X принимает значения, близкие к М.О., а Y — значения, весьма отдаленные от ее М.О.Таких примеров можно привести много: средние уровни осад­ков в разных районах, средняя заработная плата, средние ошиб­ки и т.д. Это убеждает нас в том, что знания одного М.О. мало.

Дисперсией называется матема­тическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

.

Для дискретной случайной величины дисперсия вычисляется по формуле:

.

Для непрерывной случайной величины дисперсия вычисляется по формуле:

.

Из приведенных формул следует, что размерность дисперсии есть размерность случайной величины в квадрате. Для прак­тических нужд это не всегда удобно. В этой связи чаще ис­пользуется так называемое среднеквадратическое отклонение, имеющее общепринятое обозначение .По определению

В качестве примера найдем дисперсию и среднеквадра­тическое отклонение для задачи о серии выстрелов :

Свойства дисперсии:

1.Дисперсия константы равна нулю

2.Постоянный множитель выносится за знак дисперсии в квадрате:

.

Среднее арифметическое

Одной из важных характеристик статистических данных .

является их среднее арифметическое

Пример. Рост баскетболистов, вышедших на площадку для игры, равен 201, 209, 205, 198 и 207 см. Тогда

204 =-(201 + 209 + 205+ 198 + 207) - средний рост спортсменов.

Среднее квадратичное отклонение, , где

является второй важной характеристикой выборки . Оно характеризует величину разброса значений вокруг сред­него арифметического . Если , то все одинаковы и рав­ны . Если мало, то большинство значений расположено близко от .

Вычислим среднее квадратичное отклонение роста у баскет­болистов. Имеем

откуда

Тем самым

Рассмотрим два набора чисел и

и представим их в виде последовательности точек .

Оказывается, по этой последовательности можно высказать некоторые соображения о степени связи числовых характери­стик

Для этого вычисляется коэффициент корреляции ,

где

Если число близко к 0, то говорят, что числовые характери­стики и некоррелированы или слабо коррелированы. Так будет при их независимости или слабой зависимости.

Если величина | | близка к 1 (| |< 1 всегда), то гово­рят, что величины и приближённо линейно зависимы.

Пример. Ответим на вопрос существует ли взаимосвязь между их ростом баскетболистов

( 201, 209, 205, 198 и 207) и их результативностью, если число очков соответ­ственно равно 6, 13, 10, 4 и 12?

Построим последовательность точек

по их росту и результативности и вычислим коэффи­циент корреляции. Имеем

.

Отсюда ,

Наиболее распространенные законы распре­деления вероятностей.

В рамках теории вероятностей, на основании обобщения знаний о случайных явлениях в природе и человеческом об­ществе, построен ряд моделей распределения вероятностей, которые в некоторых случаях удовлетворительно описывают исследуемые закономерности. Для каждой модели (закона распределения) установлены и условия ее применимости.

Если при рассмотрении некоторого явления исследователь считает, что имеющие место условия совпадают с условиями применимости того или иного закона, то можно воспользоваться соответствующим законом распределения и всеми знаниями о нем, накопленными в рамках теории вероятности.

1. Биномиальное распределение. Пусть реализуется схема опытов Бернулли: проводится одинаковых независимых опытов, в каждом из которых событие может появиться с постоянной вероятностью . Число появлений события в этих опытах есть дискретная случайная величина , возможные значения которой: 0; 1; 2; ... ;…; .

Законом распределения этой случайной величины может явиться формула, связывающая — число появлений события в конкретной серии из опытов с вероятностью того, что .

Такая вероятность, а следовательно, закон распределения, задается формулой Бернулли:

Числовые характеристики случайной величины , распре­деленной по биномиальному закону:

, ,

Задача. Автомобиль, подъезжая к перекрестку, может продолжить движение по любой из трех дорог А, В или С с одинаковой вероятностью. К перекрестку подъезжают пять автомобилей. Найти среднее число автомашин, которое поедет по дороге А и вероятность того, что по дороге В поедет три автомобиля.

Решение. Число автомашин, проезжающих по каждой из дорог, является случайной величиной. Если предположить, что все подъезжающие к перекрестку автомобили совершают поездку независимо друг от друга, то эта случайная величина распре­делена по биномиальному закону с и .

Следовательно, среднее число автомашин, которое проследует по дороге А, есть

, а искомая вероятность —

2. Распределение Пуассона. Пусть событие может появиться в любой момент времени. При этом выполнены следующие условия:

1) События происходят независимо друг от друга;

2) Появление события на данном отрезке времени не зависит от расположения временного отрезка на оси времени;

3) Вероятность появления события за бесконечно малый интервал времени более одного раза есть бесконечно малая величина по сравнению с

(в этой связи закон Пуассона называют законом редких событий).

Число появлений события А за выбранный промежуток времени подчиняется закону Пуассона:

Здесь — среднее число событий , появляющихся за единицу времени.

Этот закон однопараметрический, т. е. для его задания тре­буется знать только один параметр . Можно показать, что математическое ожидание и дисперсия в законе Пуассона численно равны: .

Одним из классических примеров применения закона Пуассона является описание числа запросов на соединение, поступающих на телефонную станцию.

Задача. Пусть в середине рабочего дня среднее число запросов равняется 2 в секунду. Какова вероятность того, что: 1) за секунду не поступит ни одной заявки? ,2) за две секунды поступит 10 заявок?

Решение. Поскольку правомерность применения закона Пуас­сона не вызывает сомнения и его параметр задан ( = 2), то решение задачи сводится к прямому применении формулы Пуассона : 1) ; =0,135

2) ; =0,005.

Закон Пуассона также ши­роко применяется на практике для описания реальных случайных величин, например, следующего вида: число атомов радиоактив­ного вещества, распавшихся за время Т; число заявок, поступив­ших в систему массового обслуживания за время Т; число ав­томашин, проследовавших через контрольный пункт за время Т; число опечаток в большом тексте; число бракованных изделий в крупной партии, и т.д.

Пример. Число X пожаров в городе за сутки — случайная величина, распределенная по закону Пуассона с параметром = 3. Найти вероятность, что их будет не более трех.

Р (X = 0) + Р (X = 1) + Р {X = 2) +

Р (X = 3) = +3 + + =

3. Закон равномерной плотности. Пусть непрерывная случайная величина может принимать любые значения лишь на отрезке и нет оснований считать, что появление одних возможных значений вероятней других. При выполнении этих условий говорят, что распределена с равномерной плотностью.

Случайная величина распределена на отрезке равномерно, если плотность вероятности имеет вид::

Основные числовые характеристики равномерно распреде­ленной случайной величины.

.

Рассмотрим пример. Минутная стрелка часов делает скачок на соседнее деление, когда реальное время превышает указываемое значение на полминуты. При взгляде на часы фиксируется показываемое ими время. Какова средняя ошибка в показаниях таких часов и каков разброс этой ошибки?

Решение. В каждый момент времени показания часов есть случайная величина, показывающая реальное время с некоторой ошибкой. Взгляд на часы производится в случайно выбранный момент, поэтому целесообразно предположить, что ошибка в показаниях часов имеет равномерную плотность распределения.

Так как рассогласование между реальным временем и по­казаниями часов находится в пределах от —0.5 до +0.5, то следует положить =—0.5, = +0.5. Следовательно

.

Это означает, что систематическая ошибка отсутствует:

По равномерному закону распределены ошибки округления, ошибки отсчета по приборам стрелочного типа.