1.2.4. Разбиение изображения на слои

Для построения сложных эффектов можно рассматривать изображение как наложение нескольких слоёв, то есть нескольких самостоятельных изображений. Слои перекрывают друг друга в определённой последовательности - более верхний слой накладывается нижний слой. Для получения интересующего эффекта можно производить интересующие преобразования над слоями, а затем накладывать их друг на друга и получать интересующее изображение.

Рис.22. Слои.

1.2.5. Использование масок

Иногда хочется применить фильтрацию (или другой эффект) не ко всему изображению, а только к некоторым его областям. Для этого используется маска. Маска для изображения - это дополнительное изображение такого же размера, но хранящее вместо цвета всего 1 бит на пиксель. Такой изображение можно интерпретировать как чёрно-белое изображение без оттенков серого. 1 бит на пиксель кодирует, будет ли данный пиксель изображения подвержен эффекту. Мы получаем подобие "трафарета", где значение бита "1" означает дырку в трафарете, а "0" - поверхность трафарета. На иллюстрации - образец маски и частично обработанного изображения.

Рис.23. Маска и результат применения масок

1.2.6. Афинные преобразования изображения

Афинные преобразования на плоскости - это любые преобразования, которые сохраняют прямые линии. Это означает, что при таком преобразовании любая прямая линия обязательно перейдёт в прямую линию. К афинным преобразованиям относятся сдвиг, растяжение, поворот и другие. На иллюстрации - примеры афинных преобразований.

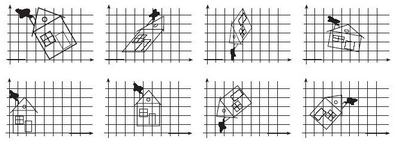
Рис.24. Афинные преобразования

Афинные преобразования могут изменять размер и форму изображения. При увеличении размера изображения теряется его резкость, а при уменьшении размера и при повороте - его детализация. После афинного преобразования можно подвергнуть изображение фильтрации - гауссовому сглаживанию. Эта процедура сделает так, что искажения не будут "бросаться в глаза". Самый простой способ осуществления афинного преобразования - использование функции, которая сопоставляет точки исходного и нового изображений.

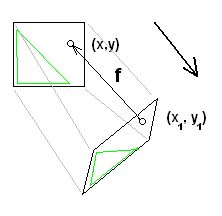
Рис.25. Афинное преобразование.

На рисунке показано преобразование, которое переводит прямоугольник в параллелограмм. Оно содержит несколько афинных преобразований - вытягивает прямоугольник, сжимает, наклоняет его, и поворачивает. Для построения результирующего изображения нужно закрасить каждый пиксель, который входит в его состав. Поэтому целесообразно использовать функцию, которая вычисляет координаты исходной точки исходя из координат результирующей точки, полученной в результате преобразования. Такую функцию легко построить на основе элементарных знаний из векторной алгебры и аналитической геометрии. Пиксель представляется в виде геометрической точки, для которой вычисляется прообраз на исходном изображении. Отыскав исходный пиксель, мы присваиваем его цвет результирующему пикселю. Координаты пикселей задаются целыми числами, а координаты абстрактных геометрических точек задаются вещественными числами. Чтобы сопоставить пиксели геометрическим точкам, мы применяем следующие способы: чтобы получить точку из пикселя, мы берём центр прямоугольного пикселя, а чтобы получить из точки пиксель, мы округляем значения координат точки, и получаем координаты пикселя как прямоугольника, внутрь которого попала точка. Укажем, как построить преобразование поворота на заданный угол. Для этого построим дополнительную систему координат, которая получена из исходной системы координат поворотом координатных осей. Поворот координатных осей на заданный угол заключается в построении ортов для новых координатных осей: Теперь по полученным ортам можно получить функцию, которая связывает точки исходного и повёрнутого изображения: