4 Условный оператор

Цель работы: приобрести навыки в решении задач с помощью условного оператора, усвоить назначение и правила его применения.

4.1 Условный оператор if

Очень часто на практике ход решение задачи зависит от выполнения какого-либо условия. В этом случае при программировании необходимо использовать условный оператор (рисунки 7,8).

В языке С существуют три возможных варианта организации ветвлений (таблица 10).

Таблица 10 – Варианта организации ветвлений

Формат условного оператора	Форма	Комментарий
If (Выражение)Оператор;	неполная форма условного оператора	Если Выражение истинно, то выполняется Оператор, если выражение ложно, то выполняется следующий за if оператор
if(Выражение)Оператор1; еlse Оператор2;	полная форма условного оператора	Если Выражение истинно, то выполняется Оператор1, если ложно – Оператор2
switch	Оператор выбора	Реализуется многоальтернативное ветвление

Выполнение оператора if начинается с вычисления выражения. Выражение в записи формата условного оператора – это некоторое условие, содержащее операции отношения и логические операции.

Операции отношения – это операции, перечисленные в таблице 11. Результатом операции отношения является целое число (0 – ложь или 1 – истина).

Таблица 11– Операции отношения

Обозначение	Значение
>	больше
>=	больше или равно
<	меньше
<=	меньше или равно
= =	равно (сравнение на равенство)
!=	не равно

Логические операции – это операции, перечисленные в таблице 12.

Таблица 12 – Логические операции

Битовые логические операции		Логические операции
&	and, и	&&	and, и
|	or, или	||	or, или
~	отрицание not, не	!	отрицание not, не
^	исключающее или, xor

Выражения (a==1) && (b>2) и (a== 1) & (b>2) с точки зрения компилятора С являются синтаксически правильными, т.к. в результате выполнения операций отношения = = и > получаются целые числа, с которыми можно производить как логическую операцию &&, так и битовую операцию &. Таблицы истинности для логических операций приведены в таблице 13

Таблица 13 – Таблицы истинности для логических операций

X	Y	X and Y		X	Y	X or Y		X	not X
1 1 0 0	1 0 1 0	1 0 0 0		1 1 0 0	1 0 1 0	1 1 1 0		1 0	0 1

Пример 4.1 Поиск наибольшего значения

Для поиска наибольшего значения из двух переменных a и b следует записать:

if (a<b) max=a

else max=b;

Задание 4.1

Напишите программу, выполняющую поиск наибольшего значения из двух переменных a и b.

Пример 4.2 Определение принадлежности точки фигуре

Напишем программу, определяющую принадлежность точки внутренней области фигуры. Пусть фигура задана ограничивающими ее прямыми (рисунок 9).

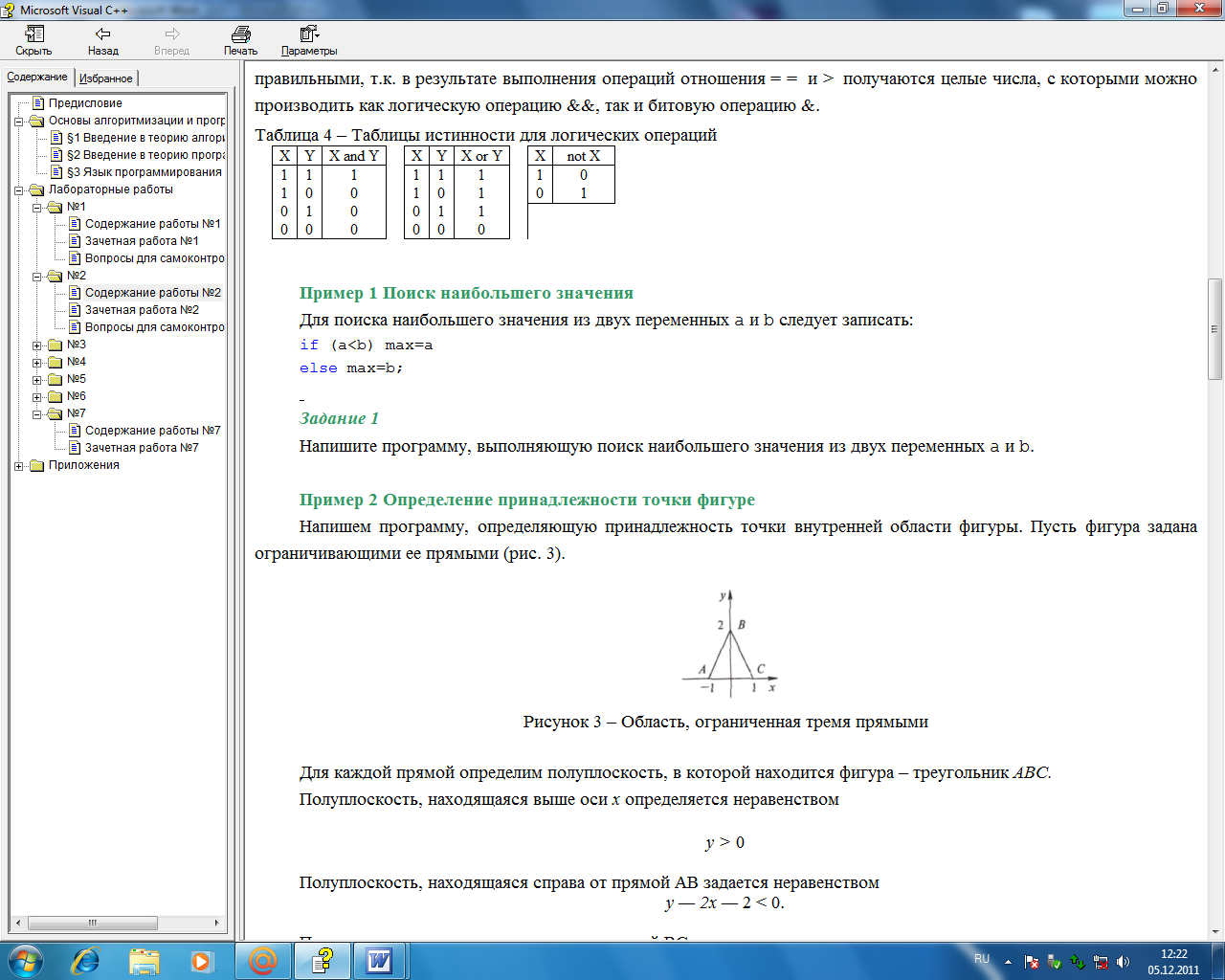
Рисунок 9 – Область, ограниченная тремя прямыми

Для каждой прямой определим полуплоскость, в которой находится фигура – треугольник АВС.

Полуплоскость, находящаяся выше оси х определяется неравенством

у > 0

Полуплоскость, находящаяся справа от прямой AB задается неравенством

у – 2х – 2 < 0.

Полуплоскость, находящаяся слева от прямой ВС за­дается неравенством

у + 1х – 2 < 0.

Условие принадлежности точки (х, у) фи­гуре:

(y > 0) and (y - 2*x - 2 < 0) and (y + 2*x - 2 < 0)

Код программы:

#include "stdafx.h"

#include<stdio.h>

#include<conio.h>

using namespace System;

int main(array<System::String ^> ^args)

{

float x,y;

printf("введите координаты точки\n");

scanf("%f%f",&x,&y);

if (y>0 & y-2*x-2<0 & y+2*x-2<0) printf("точка принадлежит области\n");

else printf("точка не принадлежит области\n");

getch();

return 0;

}

Задание 4.2

На основе примера 4.2 напишите программу, определяющую, попадает ли точка М(x, y) в круг радиусом r с центром в начале координат.