14.Типы критериальных функций в играх с природой

Рассмотрим платежную матрицу следующей структуры:

А\В	В 1	В 2
А 1	e11	e12
А 2	e21	e22
…	…	…
А n	en1	en2

УТ – утопическая точка (max, max)

АУТ - антиутопическая точка (min, min)

РТ – рабочая точ. – произвольная.

1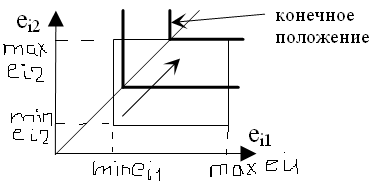 ) минимаксный критерий: - безрисковая ситуация.

Биссектриса явл-ся направляющей, вдоль к-рой перемещается линия, изображающая данную ф-ию. Наилучшим будет такое решение, точку которого данная линия касается последней.

2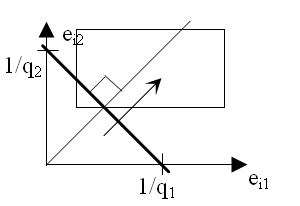 ) Критерий Байеса-Лапласа:

Риск заключается в использовании вероятностей значений. Z=ei1q1+ei2q2-это прямая

Ei1=z/q1 Ei2=z/q2

Прямую двигаем к ,последняя точка, с которой столкнется, будет наилучшее решение. Данный критерий является рискованным, поскольку при получении решении используется вероятность распределения.

3 ) Критерий Гурвица:

с – весовой коэффициент {0,1}

Это компромисс между пессимистичной позицией, отражающей минимаксный критерий, и оптимистической, отражающей критерий азартного игрока. При с=0.5 получаем линию, перпендикулярную биссектрисе (оба классических критерия берутся с единичным весом).

4 ) Критерий Ходжа – Лемана:

V– весовой множитель {0,1}

Данный критерий отражает компромисс между пессимистичной (минимаксной) и рискованной (Байеса-Лапласа). Степень зависит от V.

14.*Типы критериальных функций в играх с природой(ответ по методичке)

В задачах теории статистических решений рассматриваются платежные матрицы (для дискретного случая), либо платежная функция (в непрерывном случае). Значения в платеж. матрице, либо в платеж. функции зависят от 2х факторов: 1. состояние природы, 2. варианты решений ЛПР.

В отличие от теории игр, здесь только одна из сторон рассматривается как сторона с рациональным поведением. Др. сторона рассматривается как природный фактор с элементом неопределенности. В этом случае, условно считается, что мы играем с природой, поэтому относительно второй стороны делаются различные предположения о том, как будут выбираться варианты ее состояния.

Платежная матрица может образовываться в результате решения оптимизационной задачи когда, например, можно получить несколько эквивалентных решений. Для осуществления выбора наилучшего варианта необходимо ввести критериальную функции, отражающую систему предпочтений ЛПР.

Г еометрическая интерпретация.

E₁

F1 F2

е E2 11	е12
е21	е22
… En	…
en1	еn2

F_i – состояние природы.

Е_i – варианты решений.

Если отложить точки (e_i1, e_i2 ), то они заполнят определенное пространство, ограниченное прямоугольником. РТ – рабочая точка. Внутри этого прямоугольника образовалось 4 квадранта или 4 конуса. Рассмторим свойства точек из этих конусов.

I : все точки хотя бы по одной координате лучше, чем рассматриваемая РТ. Поэтому конус I – конус предпочтения.

III : все точки хотя бы по одной координате заведомо хуже чем РТ.

II и IV : все точки по одной координате могут быть лучше, а по другой хуже. Поэтому эти конусы – конусы неопределенности.

Для определения более менее предпочтительных точек, чем РТ, необходимо рассмотреть различные линии, представляющие линии уравнений или линии эквивалентных решений.

Линия биссектрисы (линия 1) соответствует нейтральной критериальной функции. Линия 2 – пессимистическая критериальная функция. Линия 3 – оптимистическая критериальная функция.

Любая из линий 1, 2, 3 соединяет эквивалентные по предпочтению точки. Точки, расположенные правее и выше любой из этих линий предпочтительнее точек, лежащих левее и ниже.

Предельный случай для пессимистической функции – линии, ограничивающие I-ый квадрант. Для оптимистической – III-ий квадрант.