1 курс 2009-2011 ВМС (ИТ)+Кибернетика / Типовой расчет №1 (Алгебра и геометрия), 05 вариант, ВМС(ИТ)+Кибернетика, 2009-2011
.pdfB X1 2X2 3X3 X4
Условие антиперестановочности выполнено, значит, В принадлежит
|
подпространству М. |
|
|
|
|
|
Тогда в качестве разложения по базису получим: |
|
|||
|
B 1B1 2 B2 ... k Bk , |
где |
1, 2 ,... k - некоторые скаляры из поля |
||
|
действительных чисел. |
|
|
|
|
ЗАДАНИЕ № 6 |
|
|
|
|
|
1) |
Доказать, что |
множество |
M et tet ( )t 2et t3et |
функций |
|
|
x(t), заданных |
на |
области D ( ; ) , образует |
линейное |
|
|
пространство. |
|
|
|
|
2) |
Найти его размерность и базис. |
|
|||
Решение
1)Линейное, или векторное пространство 
над полем P — это непустое множество L, на котором введены операции:
сложения, то есть каждой паре элементов множества 
ставится в соответствие элемент того же множества,
обозначаемый 
умножения на скаляр (то есть элемент поля P), то есть любому элементу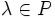 
и любому элементу 
ставится в
соответствие элемент из 
, обозначаемый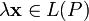 
.
Проверка:
1. Данное множество не пустое, потому как в нем есть как минимум один элемент {0}, если все коэффициенты будут равны нулю, что, в
принципе, возможно, так как D ( ; ) .
11
2. |
Если |
задать |
x (t) et tet ( )t2et t3et |
и |
|||||||||
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
x (t) |
et |
tet ( |
2 |
|
)t2et |
t3et , |
принадлежащие |
М, |
то |
функция |
|||
2 |
2 |
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
x1 (t) x2 (t)
суммы: 1et 1tet ( 1 1 )t2et 1t3et 2et 2tet ( 2 2 )t 2et 2t3et( 1 2 )et ( 1 2 )tet ( 1 1 2 2 )t2et ( 1 2 )t3et
также будет принадлежать М. |
|
|
|
|
|
|
|
3. Если домножить |
функцию x (t) et tet ( )t2et |
t3et |
на |
||||
|
1 |
1 |
1 |
1 |
1 |
1 |
|
некоторый скаляр |
из D ( ; ) , |
то |
очевидно, |
что |
функция |
||
x1 (t) 1 et 1 tet ( 1 1 ) t2et 1 t3et также принадлежит М.
4.Оба условия для линейного пространства выполнены, значит, М – линейное пространство над полем D ( ; ) .
2)Размерность М – количество всех линейно-независимых функций,
удовлетворяющих М над D ( ; ) .
Базис М – непосредственно набор линейно-независимых функций,
удовлетворяющих М над D ( ; ) .
M et tet ( )t 2et t3et
x1 t et t2et ; |
x2 t tet t2et ; |
x3 t3et |
Размерность М равна 3. |
|
|
ЗАДАНИЕ № 7
Даны векторы a OA (1, 2,5), b OB (3,1, 2), c OC (2, 1,3), d OD (6,3, 5) .
Лучи ОА, ОВ и ОС являются ребрами трехгранного угла Т.
1)Доказать, что векторы a, b, c линейно независимы.
2)Разложить вектор d по векторам a, b, c (возникающую при этом систему уравнений решить с помощью обратной матрицы).
3)Определить, лежит ли точка D внутри Т, вне Т, на одной из граней Т
(на какой?).
12
4) Определить, при каких значениях действительного параметра вектор d a , отложенный от точки О, лежит внутри трехгранного
угла Т.
Решение
1)Требуется показать, что при любых ненулевых одновременно числовых коэффициентах Х, Y и Z, что Xa Yb Zc 0 , или, что данные векторы некомпланарны.
Три вектора называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.
Данные векторы имеют общее начало в точке О. Нужно показать,
что через них нельзя провести плоскость, то есть, что их смешанное произведение не равно 0.
|
2 |
5 |
|
1 |
2 |
|
3 |
2 |
|
3 |
1 |
|
1 |
|
|
|
|
||||||||
|
|
|
|
|||||||||
3 |
1 2 |
1 |
2 |
5 |
1 26 25 2 0 |
|||||||
2 |
1 |
3 |
|
1 |
3 |
|
2 |
3 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
Что и требовалось доказать.
2) Составляем матричное уравнение:
1 |
|
2 |
|
5 x1 |
|
6 |
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
|
1 |
|
2 |
x |
|
|
3 |
|
, где |
x |
|
- коэффициенты разложения вектора |
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
3 |
x |
|
5 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
по базису. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x1 |
|
1 |
2 |
|
5 1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
3 |
|
1 2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
1 3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
5 1 |
|
|
0.5 |
|
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
6 |
|
7 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
2 |
|
|
6.5 |
3.5 |
8.5 |
|
|
6.5 |
3.5 |
8.5 |
|
3 |
|
|
92 |
|
|||
|
2 |
|
1 |
|
3 |
|
|
|
2.5 |
1.5 |
3.5 |
|
|
2.5 |
1.5 |
3.5 |
|
5 |
|
|
37 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Тогда d 7a 92b 37c - искомое разложение.
3) Проверяем условие компланарности вектора d с другими (попарно):
13
|
2 |
5 |
|
|
1 |
2 |
|
|
|
3 |
|
2 |
|
|
|
3 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
1 |
2 |
1 |
|
2 |
|
|
5 |
|
1 6 15 10 0 |
||||||||||
6 |
3 |
5 |
|
3 |
5 |
|
|
|
6 |
|
5 |
|
|
|
6 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
5 |
|
|
1 |
3 |
|
|
|
2 |
3 |
|
|
|
2 |
|
1 |
|
||
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
1 |
3 |
|
1 |
|
2 |
|
5 |
|
4 56 60 0 |
||||||||||
6 |
3 |
5 |
|
|
3 |
5 |
|
|
6 |
5 |
|
|
6 |
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значит, вектор d |
лежит на грани трехгранного угла Т, образованной |
||||
векторами |
a и c . |
||||
4) Вектор d a (6 ;3 2; 5 5) . |
|||||
Он должен быть компланарен с векторами базиса, то есть |
|||||
|
|
2 |
5 |
|
|
|
1 |
|
|
||
|
3 |
1 |
2 |
|
0 число |
|
6 |
3 2 |
5 5 |
|
|
|
2 |
5 |
|
|
|
|
1 |
|
|
||
|
2 |
1 |
3 |
|
0 такие не |
|
6 |
3 2 |
5 5 |
|
|
|
1 |
2 |
|
|
|
|
3 |
|
|
||
|
2 |
1 |
3 |
|
0 число |
|
6 |
3 2 |
5 5 |
|
|
|
|
|
|
|
|
Значит, не существуют значения действительного параметра такие, чтобы вектор лежал внутри трехгранного угла Т, так как данный вектор всегда будет принадлежать грани, образованной лучами ОС и ОВ.
14