1 курс 2009-2011 ВМС (ИТ)+Кибернетика / Типовой расчет №1 (Алгебра и геометрия), 05 вариант, ВМС(ИТ)+Кибернетика, 2009-2011

Добавил:

Fragga Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Алгебра и геометрия

Файл:

3) Проверить, что матрица

принадлежит М и

.pdf

Скачиваний:

1082

Добавлен:

26.05.2014

Размер:

495.66 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ВАРИАНТ 5

ЗАДАНИЕ № 1

Поверхность второго порядка задана уравнением : x2 ( y 1)2 2z2 4

впрямоугольной системе координат.

1)Определить тип поверхности .

2)Изобразить поверхность .

3)Нарисовать сечения поверхности координатными плоскостями.

Найти фокусы и асимптоты полученных кривых.

4)Определить по одну или по разные стороны от поверхности лежат точки M1 (0, 0, 2) и M2 (0,1, 2) .

5)Определить, сколько точек пересечения с поверхностью имеет прямая, проходящая через точки M1 и M2 .

Решение

1) : x2 ( y 1)2 2z2 4	x2	( y 1)2		z2	1.

4		4	2

Это эллипсоид, где a 2, b 2, c 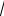2 .

Центр имеет координаты (0,-1,0). 2) Изображение поверхности:

3)Изображение сечений координатными плоскостями:

Сечением плоскостью Оxz получаем фигуру x2 2z2 3 .

		Канонический вид:				x2	z2	1	-	это эллипс в	плоскости Оxz с
		Канонический вид:				3	3	1	-	это эллипс в	плоскости Оxz с
						3	3
							2

полуосями a				и b 6		и	центром			(0,0,0). Координаты фокусов:
полуосями a			3	и b 6	2	и	центром			(0,0,0). Координаты фокусов:
					2

	6
	6	; 0; 0 . Асимптот у эллипса нет.
	2	; 0; 0 . Асимптот у эллипса нет.
	2
										фигуру ( y 1)2	2z2 4 .

			( y 1)2	z2
Канонический	вид:				1 - это эллипс в плоскости Оyz с
			4	2

				(0,-1,0). Координаты фокусов: 0;
полуосями a 2 и b		2 и центром				2;0 .

Асимптот у эллипса нет.

Сечением плоскостью Oxy получаем фигуру x2 ( y 1)2 4 .

		x2	( y 1)2
Канонический	вид:			1 - это эллипс в плоскости	Оxy с
		2	4


полуосями a 2	и b 2 и центром (0,-1,0). Координаты фокусов:					2;0;0 .

Асимптот у эллипса нет.

4)Для M1 (0, 0, 2) : 02 (0 1)2 2 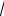2 2 5 4 , значит, точка M1 лежит вне эллипсоида.

Для M 2 (0,1, 2) : 02 (1 1)2 2 2 2 8 4 , значит, точка M2 лежит вне эллипсоида.

Значит, обе точки лежат по одну сторону от поверхности.

5)Уравнение прямой, проходящей через M1 и M2 :

						x 0
x 0	y 0	z		2
					или	y t .
0 0	1 0
			2	2


						z 2

Решаем систему:

x 0

y tz 2

x2 ( y 1)2

02 (t 1)2 2(2)2 4 (t 1)2 0 t 1.

2z2 4

Тогда точка пересечения прямой и поверхности только одна и имеет

координаты (0, 1, 2) .

ЗАДАНИЕ № 2

Дано комплексное число z 5 5i .

3 i 3

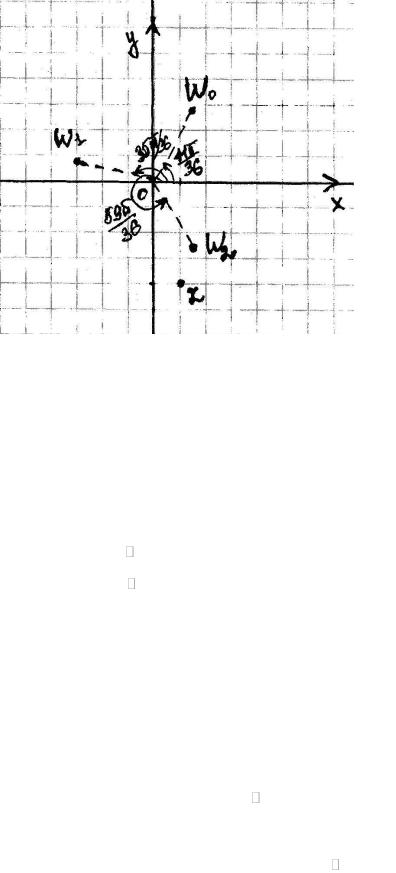
1)Записать число z в показательной, тригонометрической и алгебраической форме, изобразить его на комплексной плоскости.

2)Записать в показательной, тригонометрической и алгебраической форме число u z 8 .

3)Записать в показательной и тригонометрической форме каждое значение wk (k 0,1, 2) корня степени m=3.

4)Изобразить число z и числа wk на одной комплексной плоскости.

Решение

1) Алгебраическая форма числа:


		5 5i											( 5 5i)(3 i											3)					15 15i 5										3i 5		3			15 5 3			15 5	3
	z																																					9 3											i

		3	i												i				3)(3 i					3)																				12			12
		3	i		3 (3										i				3)(3 i					3)																				12			12

				15 5														2										2
				15 5												3		2			15 5 3							2						5 6
	z
	z
									12													12												6
									12													12												6
													15 5
													15 5						3
																																					11
																	12
																	12
arg z arctg																							arctg(						3 2)
											15 5																											12
											15 5									3																		12
																	12
Тригонометрическая форма числа:
												11										11
	z	5	6									11						i sin				11
						cos																		.
						cos																		.
			6										12									12
Показательная форма числа:
								11
		5	6				i	11
		5	6				i
	z					e 12 .
	z		6			e 12 .
			6
2) По формуле Муавра тригонометрическая форма числа:
																			11							11					8								8			22			22
			8						5 6										11							11					8							5 6	8			22			22
u z														cos									i sin																	cos				i sin		.
u z														cos									i sin																	cos				i sin		.
										6									12								12											6					3		3
Показательная форма числа:
																	11		8				5				8						22
									5 6							i									6								22		i
									5 6							i									6										i
u z 8														e			12													e				3		.
u z 8									6					e			12							6						e				3		.
									6															6
																																4

Алгебраическая форма числа:

	15 5
			3	15 5 3
u z 8

		12		12

	8
	i .

3) В тригонометрической форме:

														11				2 k									11		2 k
														11													11
							5			6
														12													12

w	3 z 3										cos												i sin												, k	0,1, 2
w	3 z 3										cos												i sin												, k	0,1, 2
k							6											3											3
							6											3											3


Тогда
												11									11															35		35

	w0					5 6											i sin									w1				5 6							i sin
				3						cos														,					3				cos						,
				3			6			cos		36												,					3	6			cos			36			,
							6					36										36								6						36		36
												59										59

	w2					5	6										i sin
				3						cos															.
				3			6			cos		36													.
							6					36										36
В показательной форме:
													11				2 k
													11
				5				6	exp i													,
													12
w 3		z 3											12											k 0,1, 2
w 3		z 3																						k 0,1, 2
k						6										3
						6										3


Тогда
				11																35												59

	5 6														5 6													5 6
w 3							i ,			w 3												i ,		w 3										i .
w 3			e		36		i ,			w 3									e 36			i ,		w 3							e 36			i .
0	6									1		6												2					6
	6											6																	6

ЗАДАНИЕ № 3

Дан многочлен p(z) 5z4 8z3 3z2 2z 2 .

1)Найти все (целые) корни многочлена p(z). Записать каждый корень в алгебраической форме, указать его алгебраическую кратность.

2)Разложить многочлен p(z) на неприводимые множители:

а) в множестве			комплексных чисел;
б) в множестве			действительных чисел.
Решение
1) 5z4 8z3 3z2 2z 2 (5z3					3z2 2)(z 1) (5z2		2z 2)(z 1)2
Корни многочлена в алгебраической форме:
z1 1		кратность 2
z2	0, 2 0, 6i		кратность 1.
z3 0, 2 0, 6i			кратность 1
2) а)	разложение в множестве					комплексных чисел:
p(z) 5z4 8z3			3z2	2z 2 (z 1)(z 1)(z 0, 2 0,6i)(z 0, 2 0,6i)
б)	разложение			в	множестве		действительных чисел:
p(z) 5z4		8z3	3z2	2z 2 (5z2		2z 2)(z 1)(z 1)
						6

ЗАДАНИЕ № 4

Пусть Pn – линейное пространство многочленов степени не выше n с

действительными коэффициентами. Множество M Pn состоит из всех тех многочленов p(t), которые удовлетворяют условию p(2 - i) = 0.

1)Доказать, что множество М – подпространство в Pn.

2)Найти размерность и какой-либо базис подпространства М.

3)Дополнить базис подпространства М до базиса Pn.

Решение

1)Теорема: Критерий подпространства. Непустое множество 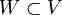является подпространством пространства V тогда и только тогда, когда

W замкнуто относительно сложения векторов и умножения их на скаляры. Иными словами, выполняются следующие два условия: 1. 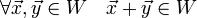; 2. .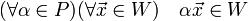

Проверка условий:

1.Пусть p1(t) и p2(t) – некоторые многочлены степени не выше n с

действительными коэффициентами, для которых выполняется

условие p1(2 - i) = p2(2 - i) = 0, то есть они принадлежат М. Тогда очевидно, что многочлен (p1(t) + p2(t)) тоже принадлежит М, так как для него будет выполняться заданное условие.

2. Если некоторый скаляр , принадлежащий множеству , умножить на некоторый многочлен p(t) из М, то многочлен ( p(t)) очевидно тоже будет принадлежать М.

Критерий подпространства для М выполняется, что и требовалось доказать.

2)Размерность М – это количество линейно-независимых многочленов степени не выше n с действительными коэффициентами p(t), которые удовлетворяют условию p(2 - i) = 0, то есть, dim(M) n.

Базис М – это набор линейно-независимых многочленов степени не выше n с действительными коэффициентами p(t), которые удовлетворяют условию p(2 - i) = 0, то есть (p1(t), p2(t), …, pk(t)), где k n.

Общий вид многочленов из P3: p x a1 ia2 x3 b1 ib2 x2 c1 ic2 x d1 id2 .

Составим общий вид многочленов из М:

p 2 i 2a1 11a2 11ia1 2ia2 3b1 4b2 4b1i 3ib2 2c1 c2 ic1 2ic2 d1 id2 0

2a1 3b1 2c1 11a2 4b2 c2	0			c1 a1 1.5b1 5.5a2 2b2			0.5c2
	2c2 d2	0			10a1 2.5b1	d2 7.5a2	5b2 2.5c2
11a1 4b1 c1 d1 2a2 3b2	2c2 d2	0		d1	10a1 2.5b1	d2 7.5a2	5b2 2.5c2
p x a1 ia2 x3 b1 ib2 x2 a1 1.5b1			5.5a2		2b2 0.5c2	ic2 x 10a1 2.5b1
d2 7.5a2 5b2 2.5c2 id2
Тогда размерность М равна 6. Найдем базис М:
p x a1 ia2 x3 b1 ib2 x2 a1		1.5b1		5.5a2 2b2 0.5c2 ic2 x 10a1 2.5b1
d2 7.5a2 5b2 2.5c2 id2
p1 x x3 x 10
p2 x ix3 5.5x 7.5

p3 x x2 1.5x 2.5 p4 x ix2 2x 5

p5 x 0.5 i x 2.5 p6 x i

3)Чтобы дополнить базис подпространства М до базиса Pn, нужно дописать в набор, описанный выше, линейно-независимые векторы

	p7	x 1
pm(t) такие, что pm(2-i)≠0, где k≤m≤n. Пусть	p8	x x 1.

ЗАДАНИЕ № 5

1) Доказать,	что		множество М			матриц, антиперестановочных с
	0		1	0
матрицей		1	0	0	, образует	подпространство в пространстве
	A
		0	0	1

Мm*n всех матриц данного размера.

2) Найти размерность и построить базис М.

разложить ее по базису в М.

Решение

1)Матрицы называются антиперестановочными, если АВ = - ВА.

Матрицы можно перемножать, если количество строк первого множителя равно количеству столбцов второго.

Значит, М – множество матриц размерности 3*3, которые удовлетворяют критерию антиперестановочности.

Для всех элементов М будут выполняться условия критерия подпространств о сумме нескольких элементов (матрицы одинаковой размерности можно складывать, свойство матрицы суммы не изменится) и умножении элемента на скаляр (размерность и свойство при этом не изменятся), значит, М – подпространство в пространстве М3*3 всех матриц.

2)Размерность М – это количество всех линейно-независимых матриц

3*3, которые удовлетворяют условию АВ = - ВА, пусть их будет K и

тогда K≤N, где N – размерность пространства М3*3 всех матриц.

3)Базис М – линейно-независимые элементы, удовлетворяющие условию АВ = - ВА, то есть множество (В1, В2, …, Вk), где K≤N.

Пусть

a	b	c
X d	e	f

	h
g	h	k

Найдем общий вид матрицы Х, удовлетворяющей указанному уравнению.

0		1	0	a b	c	a b	c 0		1	0
	1	0	0	d e	f	d e	f	1	0	0

	0	0	1					0	0	1
	0	0	1	g h	k	g h	k	0	0	1

d			e		f				b	a	c
a b					c		e			d f

			h		k					g
g			h		k				h	g	k
d b
e a
		c					d b
f		c					d b
a e							a e

		d							c
b		d					f		c
c f							g h
	g h								0
	g h							k	0
h g
h g
		k
k		k

			e				b		c
X				b			e		c
X				b			e		c

				h		h			0
				h		h			0

Итак, размерность М равна 4. Найдем базис М, придавая по очереди одному

из чисел значение 1, а остальным 0:

		1		0	0				0		1	0				0 0			1				0		0	0
X			0	1	0	;	X			1	0	0	;	X			0	0	1	;	X			0	0	0
	1							2							3							4
			0	0	0					0	0	0					0	0	0					1	1	0
			0	0	0					0	0	0					0	0	0					1	1	0

0 1 0 1			2	3		2 1		3
1 0 0		2 1 3				1 2			3
1 0 0		2 1 3				1 2			3

4) АВ= 0 0 1		1	1	0		1 1			0
1 2		3 0		1	0	2	1		3
2	1 3		1	0	0	1 2 3
2	1 3		1	0	0	1 2 3

ВА = 1	1	0	0	0	1	1	1		0

1 / 21 2 > Следующая >>>

d			e		f				b	a	c
a b					c		e			d f

			h		k					g
g			h		k				h	g	k
d b
e a
		c					d b
f		c					d b
a e							a e

		d							c
b		d					f		c
c f							g h
	g h								0
	g h							k	0
h g
h g
		k
k		k

			e				b		c
X				b			e		c
X				b			e		c

				h		h			0
				h		h			0

		1		0	0				0		1	0				0 0			1				0		0	0
X			0	1	0	;	X			1	0	0	;	X			0	0	1	;	X			0	0	0
	1							2							3							4
			0	0	0					0	0	0					0	0	0					1	1	0
			0	0	0					0	0	0					0	0	0					1	1	0

d			e		f				b	a	c
a b					c		e			d f

			h		k					g
g			h		k				h	g	k
d b
e a
		c					d b
f		c					d b
a e							a e

		d							c
b		d					f		c
c f							g h
	g h								0
	g h							k	0
h g
h g
		k
k		k

			e				b		c
X				b			e		c
X				b			e		c

				h		h			0
				h		h			0

		1		0	0				0		1	0				0 0			1				0		0	0
X			0	1	0	;	X			1	0	0	;	X			0	0	1	;	X			0	0	0
	1							2							3							4
			0	0	0					0	0	0					0	0	0					1	1	0
			0	0	0					0	0	0					0	0	0					1	1	0

d			e		f				b	a	c
a b					c		e			d f

			h		k					g
g			h		k				h	g	k
d b
e a
		c					d b
f		c					d b
a e							a e

		d							c
b		d					f		c
c f							g h
	g h								0
	g h							k	0
h g
h g
		k
k		k

			e				b		c
X				b			e		c
X				b			e		c

				h		h			0
				h		h			0

		1		0	0				0		1	0				0 0			1				0		0	0
X			0	1	0	;	X			1	0	0	;	X			0	0	1	;	X			0	0	0
	1							2							3							4
			0	0	0					0	0	0					0	0	0					1	1	0
			0	0	0					0	0	0					0	0	0					1	1	0