4. Свойства абсолютно сходящихся рядов

Свойство 1: Если ряды и абсолютно сходятся, то ряд так же абсолютно сходится

Свойство 2: Если ряд абсолютно сходится, то ряд, составленный из тех же членов, но взятых в другом порядке, так же абсолютно сходится, причем к той же сумме.

Свойство 3: Если ряды и абсолютно сходятся к суммам и соответственно, то ряд, составленный из всевозможных попарных произведений членов этих рядов, расположенных в порядке, также абсолютно сходится и его сумма равна

Теорема Римана (о перестановке членов неабсолютно сходящегося ряда)

Если ряд сходится условно, то каким бы ни было число A, можно так переставить члены ряда, что сумма полученного ряда будет равна A

Замечание: Можно сделать ряд расходящимся

Функциональные ряды.

1) Основные определения.

Рассмотрим последовательность функций . с общей областью определения Е.

Определение 1. (1) называется функциональным рядом.

Пример 1. Здесь .

Пусть точка . Тогда ряд (1) в точке обращается в числовой ряд (2):

, который может сходиться или расходиться.

Определение 2. Совокупность всех значений переменной х, для которых

функциональный ряд (1) обращается в сходящийся числовой ряд, называется

областью сходимости функционального ряда.

Или: . Если , то - сумма ряда в

точке .

) Равномерная сходимость функционального ряда.

Определение 1. Последовательность функций с общей областью

определения называется равномерно сходящейся к функции не множестве

, если .

Обозначение: ; - предельная функция последовательности.

Определение 2. Функциональный ряд сходится к сумме равномерно

на множестве Х, если последовательность его частичных сумм сходится

равномерно к на Х. Записывают так:

последовательность частичных сумм сходится к S равномерно на Х.

функциональный ряд сходится к сумме S в области D.

функциональный ряд сходится равномерно к S на множестве .

Признак равномерной сходимости.

Определение 1. Числовой знакоположительный сходящийся ряд

называется мажорантой на множестве Х для функционального ряда , если

.

Теорема (признак Вейерштрасса): Если функциональный ряд имет на

множестве Х мажоранту, то он сходится равномерно на Х.

4) Методы построения мажоранты.

1) использование св-ва ограниченности ф-ций

. .

2) использование св-ва монотонности

а) [1/3;3] т.к. функция монотонно

возрастает на данном отрезке - мажоранта на этом множестве.

б) - сходящийся ряд на , ,

3) использование неравенства

- равномерно сходится на . .

4) нахождение максимума функции

а) .

б) сходится равномерно на .

Здесь неравенство (3) неприменимо. .

. - мажоранта на .

Замечание: при х<0, .

5) использование св-в геометрической прогрессии.

. Область определения . Сходится равномерно на

тогда это уже будет убывающая геометрическая прогрессия,

- мажоранта. Кстати, .

6) Ряд сходится равномерно на , но признак Вейерштрасса здесь

не работает. , но не может быть мажорантой, т.к. расходится.

Поступим по определению: , ,

сходится равномерно на .

Свойства равномерно сходящихся функциональных рядов.

1. Непрерывность суммы равномерно сходящегося ряда

Теорема 1:

1)

2)-непрерывна в

1), 2) - непрерывна в

2. Действие с равномерно сходящимися рядами

Теорема (о почленном интегрировании равномерно сходящегося ряда)

1) (непрерывна на )

2)

1), 2)

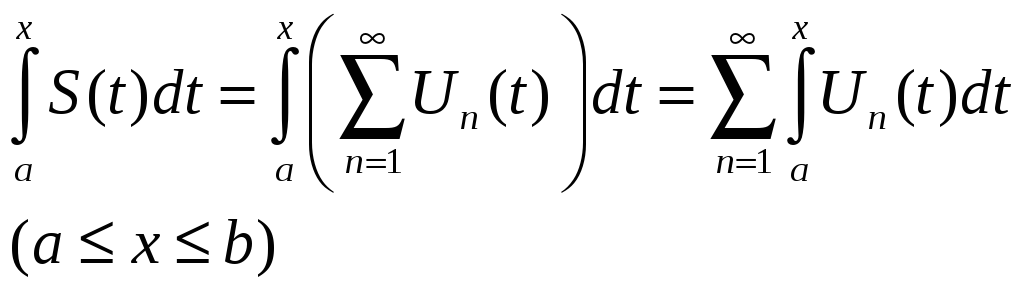
Теорема (о почленном дифференцировании функционального ряда):

1)

2) сходится в

3)

1) 2) 3)

Теорема (о линейной комбинации равномерно сходящихся рядов):

Теорема (о предельном переходе):

1) определена в и для

2)

а) - числовой ряд сходится

б)

Замечание: Из этой теоремы легко следует Т.1 (о непрерывности суммы)