Числовые ряды.

1) Сходящийся ряд и его сумма.

Рассмотрим последовательность действительных чисел {a_n}

(a_n  R  n).

Опр. 1 Выражение вида a₁+a₂+...+a_n+... называется числовым

рядом. В данном ряду a₁, a₂,.. являются членами ряда. Выражение

a_n=f(n) – общий член ряда, являющееся функцией натурального

₀₀

аргумента. Сокращенная запись ряда: a₁+a₂+...+a_n+...= a_n .

ⁿ⁼¹

Опр. 2 Сумма первых n членов ряда называется n-ой

частичной суммой ряда, т. е.

_n

S_n = a₁+a₂+...+a_n = a_k

^k=1

S₁=a₁, S₂=a₁+a₂, S_n=a₁+a₂+...+a_n.

{S_n} – числовая последовательность частичных сумм.

Опр. 3 (главное!) Если существует lim S_n = S = оо, то ряд

_оо ^n->оо

 a_n называется сходящимся, а число S – его суммой (S -

ⁿ⁼¹

конечное число).

Если lim S_n = оо или не существует, то ряд называется

^n->оо

расходящимся.

Опр. 4 Ряд, полученный из данного отбрасыванием первых m

Членов, называется m-ым остатком ряда и обозначается r_m:

_{oo oo}

a₁+a₂+...+ a_m+a_m+1+... , т. е. r_m =  a_n. Т. о.  a_n = S_m + r_m

^{n=m+1 n=1}

Утверждение 1 Если ряд сходится, то любой его остаток

тоже сходится.

Утверждение 2 Если сходится хотя бы один остаток ряда, то

сходится и сам ряд.

Следствие из Утв. 1 и утв. 2: отбрасывание конечного числа

членов ряда не влияет на характер его сходимости, но в

случае сходимости ряда сумма меняется.

Утверждение 3 Остаток сходящегося ряда стремится к нулю,

_оо

т. е. если  a_n – сходится, то lim r_m = 0.

1. ^n->oo

2) Геометрическая прогрессия

Это важный случай числового ряда. a_n=a_oq^n-1, qR ( q = 1) –

знаменатель прогрессии.

_оо

 a_n = a_o+a_oq+a_oq²+...+a_oqⁿ+...

ⁿ⁼¹

Если |q| > 1, то lim S_n=lim(( q/(1-q) ) – ( qⁿ⁺¹/ (1-q) ))=oo =>

^{n->oo n->oo}

прогрессия расходится.

Если |q| < 1, то lim S_n=lim( ( q/(1-q) ) – ( qⁿ⁺¹/ (1-q) ) ) =

^{n->oo n->oo}

= (q/(1-q)) = const => прогрессия сходится.

Аналогично для a_o = q.

Итак, _oo

 a_oq^n-1 |q| < 1 сходится и S = (a_o/(1-q))

ⁿ⁼¹

|q| > 1 расходится

3) Необходимый признак сходимости ряда

_oo

Т. Если ряд  a_n сходится, то lim a_n = 0

^{n=1 n->oo}

Следствие. Если не существует lim a_n или существует lim a_n = 0,

^{n->oo n->oo}

то ряд заведомо расходится, т. к. если бы он сходился, то

lim a_n = 0

^n->oo

4) Критерий Коши сходимости ряда.

_oo

Теорема 1 (без доказательства). Ряд  a_n сходится <=> 

ⁿ⁼¹

существует такое N():  n >= N() и  p  N:

|a_n+1 + a_n+2 +...+ a_n+p| < 

Теорема 2 (отрицание критерия Коши).

Если существует :  k  N и существуют n>=k и p  N:

|a_n+1 + a_n+2 +...+ a_n+p| >= .

_oo

Итак, ряд (1/n),называющийся гармоническим рядом, расходится.

ⁿ⁼¹

5) Обобщенный гармонический ряд.

Опр. Ряд вида  (1/n^) () называется обобщенным

ⁿ⁼¹

гармоническим рядом или рядом Дирихле. Мы показали, что при

=2 он сходится, а при =1 расходится. Позже мы докажем, что

_oo  > 1 сходится

(1/n^)

ⁿ⁼¹ 0 <  <= 1 расходится

_{oo oo}

 (1/n) расходится  (1/(nn)) сходится

^{n=1 n=1}

=1/2<1 =3/2>1

_oo

 (1/(³n⁷)) сходится

ⁿ⁼¹

=7/3>1

6) Комплексные числовые ряды.

Z_n = a_n + ib_n, a_n – действительная часть, b_n – мнимая часть.

 Z_n =  (a_n + ib_n)

Такой ряд сходится <=> сходятся ряды из его действительной и

мнимой частей:  Z_n <=> a_n, b_n

Геометрическая прогрессия с комплексными числами: С₀, qC

_{oo oo}

С_n = С₀q^n-1, |q| > 1 => расходится

^{n=1 n=1} |q| < 1 => сходится

q = q₁ + iq₂ => |q| = (q²₁ + q²₂)

1. Действия над сходящимися рядами

Теорема 1: Если ряд сходится и его сумма равна S, то ряд , где - const, тоже сходится и его сумма S, т.е.

Теорема 2: Запишем формулировку кратко:

Следствие из Т.1 и Т.2:

Это свойство линейности сходящихся рядов.

Замечание: Что можно сказать о сходимости ряда , где , если известно, что

1) - сходится, - расходится

2) и - оба расходятся?

В первом случае - расходится, а во втором может как сходиться, так и расходиться.

Теорема 3: Если ряд сходится, то можно группировать его слагаемые, не меняя их местами, получится ряд, сходящийся к той же сумме.

2. Ряды с положительными членами

(Положительные ряды, знакоположительные ряды, ряды-синонимы)

Определение: Ряд называется знакоположительным, если и , т.е. все его члены действительные, неотрицательные числа.

Теорема (Критерий сходимости ряда с неотрицательными членами)

Ряд сходится последовательность , т.е. или

3. Признаки сравнения рядов с неотрицательными членами

Теорема 1 (Первый признак сравнения)

Если , то

Если сходится, то - сходится

Если расходится, то - расходится

Теорема 2 (Предельная форма признака сравнения или II-ой признак сравнения) Пусть и

Тогда

1) и сходится или расходятся одновременно

2) из сходимости сходимость

3) из сходимости сходимость

Замечание: Удобно сравнивать с известными рядами

и

4. Признаки Даламбера и Коши в предельной форме

Теорема 1 (Признак Даламбера)

Если для ряда : , то

Теорема 2 (Радикальный признак Коши)

Если для ряда : , то

по асимптотической формуле Стирлинга:

Интегральный признак Коши

1. Теорема (интегральный признак)

Пусть функция f(x) принимает положительные значения и является монотонно убывающей ( ) и пусть .Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

1) Если ингеграл сходится, то

ряд сходится (по критерию сходимости

знакоположительных рядов).

2) Если интеграл расходится, то - неогр. =>

ряд расходится.

3) Аналогично в другую сторону. Если ряд сходится, то

и интеграл сходится.

4) Если ряд расходится, то .

2. Исследование поведение обобщенного гармонического ряда с помощью интегрального признака.

.

3. Оценка остатка знакоположительного ряда с помощью интегрального признака.

Из доказательства теоремы пункта 1 следует, что

1) . Это оценка суммы ряда.

2) . Это оценка остатка ряда (остаток - это ряд

с первым членом , далее как в 1) ).

6. Понятие об абсолютной сходимости.

Ряд с вещественными или комплексными членами (т.е. не

знакоположительный) называется абсолютно сходящимся, если сходится ряд из

абсолютных величин (модудей) его членов: (знакоположительный).

Абсолютная сходимость более сильная, чем простая сходимость, т.е.

1) Если ряд сходится абсолютно, то он сходится

2) Если ряд сходится, то это не означает, что он сходится абсолютно.

К этому понятию мы подробнее обратимся позже, а сейчас только отметим,

что для исследования на абсолютную сходимость применяются признаки сх-ти

положительных рядов.

1. Знакочередующийся ряд Лейбница

Опр. Ряд называется знакочередующимся, если члены ряда попеременно положительны и отрицательны.

Пример:

Если

Теорема: (Признак Лейбница)

Если ряд такой, что:

1) (знакочередование)

2) (монотонное убывание)

3) ,

то ряд сходится и его сумма

Замечание: Ряд, удовлетворяющий теореме, называется рядом Лейбница или лейбницевский рядом.

Примеры лейбницевских рядов:

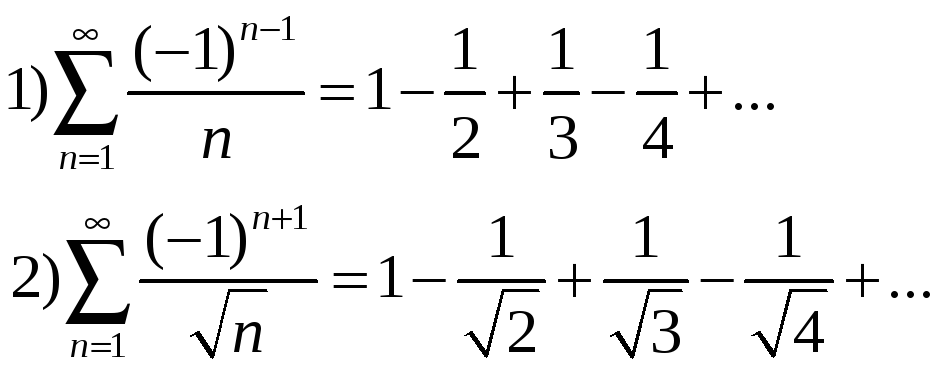
2. Оценка остатка ряда Лейбница

Рассмотрим ряд Лейбница и выделим в нем частичную сумму т остаток :

,

т.е.

остаток - тоже ряд Лейбница его сумма < по модулю его первого члена

Следствие: Если в ряде Лейбница заменить его сумму на n-ую частичную сумму (т.е. отбросить остаток ), то допущенная ошибка не превзойдет по абсолютной величине модуля первого отброшенного члена.

3. Абсолютная и неабсолютная сходимость вещественного и комплексного ряда.

Рассмотрим ряд ; имеет произвольный знак и может быть даже комплексным числом

Опр.: Ряд называется абсолютно сходящимся, если сходится ряд из его модулей

Напомним, что

Ряд знакоположительный вещественный ряд к его исследованию применимы все изученные ранее признаки сходимости знакоположительных рядов.

Опр.: Если ряд сходится, а расходится, то ряд называет условно сходящимся.

Теорема: (Сходимость ряда из модулей как достаточное условие сходимости исходного ряда)

Если ряд абсолютно сходится, то он и просто сходится.

Если ряд - сходится, то - сходится