Вопрос №1. Основные понятия вычислительной математики.

Численные методы. Решение подавляющего большинства инженерных и научно-технических задач в настоящее время тесно связано с применением вычислительной техники и основывается на описании реальных процессов математическими моделями, которые представляют собой совокупности обычных, интегральных и дифференциальных уравнений.

Всякая математическая модель представляет собой математическое преобразование вида

Y=F(x,u)

где x = (x1,...,xn) - совокупность входных параметров;

y = (y1,...,yn) - совокупность выходных параметров объекта;

U = (U1,...,Un) - совокупность входных управляющих воздействий, с помощью которых осуществляется управление процессами;

F - оператор преобразования.

Для решения математических задач в САПР применяются три группы методов: графические, аналитические, численные.

Графические методы предполагают искать решение с помощью геометрических построений.

Аналитические методы предполагают искать решение задачи в виде формулы.

Численные методы являются основными методами в САПР. В их основе лежит процедура сведения решения задачи к конечному числу арифметических действий над числами, и получить результат в виде численных значений.

Основные требования и показатели численных методов:

1) устойчивость;

2) сходимость;

3) эффективность (скорость сходимости);

4) погрешность.

Алгоритм считается устойчивым, если он обеспечивает нахождение существующего и единственного решения при различных исходных данных.

Сходимость является основным критерием оценки алгоритма. Алгоритм сходится, если итерационная последовательность приближений.

x¹,x²,...,x^k x^* , k   , т. е.

Скорость сходимости. (эффективность) – обозначает количество итераций, затраченных алгоритмом для достижения приемлемой точности решения задачи. Сущ. 3 оценки скорости сходимости: линейная и сверх линейная. Пусть x^kx^* , k  

Говорят, что алгоритм обладает линейной скоростью сходимости, если g э [0;1] и R0

|x^k+1-x^*|g_k |x^k-x^*| , при kk₀

Алгоритм обладает сверх линейной скоростью сходимости, если выполняется условие

|x^k+1-x^*|g_k |x^k-x^*| , g 0 , k  

Алгоритм обладает квадратичной скоростью сходимости, если

|x^k+1-x^*|c |x^k-x^*| , c 0

ВОПРОС №2. Решение не линейного уравнения методом простейшей итерации. Понятие сжимающего отображения. Теорема о сходимости метода. Геометрическая интерпретация.

Алгоритмы решения нелинейного уравнения. Метод итераций.

Пусть требуется решить уравнения вида f(x)=0 (*), где f(x) - непрерывная функция.

Чтобы методом итераций найти решение уравнения (*) его необходимо преобразовать к виду

x⁽¹⁾ = (x⁽⁰⁾) (**)

Зададим начальное приближение x₀ и подставим его в правую часть уравнения (**).

Получим значение х₁

Подставив значение х₁ в правую часть уравнения (**) получим х₂

Продолжая этот процесс, неограниченно получим последовательность приближений к корню

x^k+1=(x^k) , k 0 (***)

Условие сходимости метода. Теорема. Пусть в некоторой  - окрестности корня х^* функция (x) непрерывна и дифференцируема и удовлетворяет неравенству | ' (x)| g, (5) где 0 < g < 1 - константа. Тогда независимо от выбора начального приближения х⁽⁰⁾ из указанной  - окрестности корня итерационная последовательность не выходит из этой окрестности и справедлива следующая оценка погрешности: Неравенство (5) означает, что метод простой итерации обладает линейной скоростью сходимости.

Геометрическая интерпретация метода. На рис.1 (а) видно, что корень уравнения (1) является абсциссой точки пересечения графиков двух функций y = x и y =  (x). В случаях (а) и (б) метод простой итерации сходится при произвольном начальном приближении. В случаях (в) и (г) метод расходится при любом начальном приближении. Замечено, что в случаях (а) и (б)    (x)  < 1, а в случаях (в) и (г)    (x)  > 1.

Сжимающее отображение. Понятие с.о. позволяет решать вопрос о сходимости итерационного процесса аналитически, а не геометрическими построениями. Возьмем непрерывную  (x), заданную на отрезке  a; b . Каждой т. x   a; b соответствует y =  (x ) на оси ординат.

Т.е. функция  (x) задает отображение отрезка  a; b на оси ординат. Чтобы сравнить образ отрезка с самим отрезком необходимо отобразить точки на оси 0y через прямую y = x на ось 0x. Если образ отрезка  a; b  является частью  a; b , то  (x) отображает  a; b в себя. Построим последовательность  a; b ;  a ; b  ;  a ; b  и т.д. Если после каждого отображения отрезок уменьшается в М>1 раз, то отображение называется сжимающим.

Расстояние между двумя т. x1 и x2 =  x2 - x1  . Условие сжатия формулируется: отображение  (x) является сжимающим на отрезке  a; b , если существует 0<x<1 и для любых двух точек x1 , x2   a; b выполняется неравенство:

  (x2 ) -  (x1 )    x2 - x1  ,  = 1/М.

ВОПРОС №3. Уравнение МПИ. Условие на выбор числа r. Геометрическая интерпретация.

Модификация итерационного процесса.

Применение метода итераций x =(x); часто затрудняется тем, что  (x) несжимающая функция. Помимо этого можно потребовать увеличение скорости сходимости.

Рассмотрим исходное уравнение

f (x) = 0, (1) где f (x) =  (x) – x. Решение x итерационного процесса будет и решением (1).

Преобразуем (1) следующим образом f (x) = 0  r f (x) = 0  x = x + r f (x) или x =  (x) (2)

где f (x) = x + r f (x), r  0.

Итерационный процесс происходит по формуле

x =  (x ) или x = x + r f (x ),  = 0,1,2, ... (3)

Решение (2) является решением (1).

В предложенном варианте существование решения и сходимость x , x , x , ... , x , ... обеспечивается условиями теоремы сжатия относительно  (x). При этом r может быть выбрана таким методом, что условие сжатия выполняется для  (x) в тех случаях, когда  (x) несжимаема.

Пусть    (x)  >1 для итерационного процесса x =  (x). Будем искать решение (1) решая (2) с помощью алгоритма (3), а число r выберем из условия сжатия для  (x) при x = x*.

   (x*) < 1, или  1+ r f  (x*) < 1,  1+ r(  (x*) – 1)  < 1 (4)

-1<1+ r(  (x*) – 1) < 1 

 -2< r(  (x*) – 1) < 0

 -2/  (x*) – 1< r< 0,

r< 0 и  r < 2 /  (x*) – 1, если   - 1> 0

r> 0 и  r < 2 /  (x) – 1, если   - 1> 0

Из условия сжатия функции  (x) получим рекомендации для выбора числа r в уравнении (2) и алгоритма (3), обеспечивающих сходимость (3). Можно потребовать наиболее сильного сжатия,   (x*) = 0 (5) Отсюда получаем значение r = -1/   (x*) – 1 (6)

Геометрическая интерпретация.

Касательная в т. Bn y – f(x ) = f (x )(x-xn ).

ВОПРОС №4. Метод Ньютона для решения не линейного уравнения. Условие сходимости метода. Геометрическая интерпретация.

Метод Ньютона. В предложенной методике есть недостаток: r = const на протяжении всего процесса поиска корня. Однако нет препятствий для изменения этого значения в процессе выполнения итерационного процесса. Сделаем r функцией x и подставим в алгоритм:

x = x + r(x ) f (x ), n = 0,1,2, ... .(7)

Потребуем, чтобы   (x) была = 0 в достаточно большой окрестности корня x*:

  (x) = 1 + r f  (x) = 0,

отсюда r(x) = -1/ f  (x) = -1/  (x) –1.

Тогда алгоритм будет иметь вид:

x(n+1) = x^(к) - f(x^(к)) / f  (x^(к)) – метод Ньютона.

Условие сходимости метода. Для вывода сходимости метода потребуем сжатия функции (x)=x-f(x) / f ‘(x) на произвольном отрезке: x ∊ [a;b]. Если ф-я f(x) – сжимающая, то для люб. x₀, x₁ из отрезка [a;b] должно происходить уменьшение длины (x₁ – x₀) при каждом новом отображении ф-и (x). Запишем условие сжатия след. образом:

В ф-ле сжимающегося отобр-я x<1 отсюда если вып. M/m*|x₁-x₀|<1, то метод сходится. |x^k+1-x^*|  M / m |x^k-x^*|²

Геометрическая интерпретация.

Касательная в т. Bn y – f(x ) = f (x )(x-xn ).

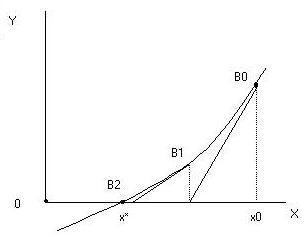
ВОПРОС №5. Метод секущих. Условие сходимости. Геометрическая интерполяция.

Метод секущих. Полагая y = 0, x = xn+1 получим формулу для метода Ньютона. Если значения производной вычислять приближенно, как приращение f(x) в т. x и xn-1, то получим метод секущих.

При условии x = x и y(x) = 0 получим (1).

Оценка скорости сходимости (***).

Условие сходимости метода. Для вывода сходимости метода потребуем сжатия функции (x)=x-f(x) / f ‘(x) на произвольном отрезке: x ∊ [a;b]. Если ф-я f(x) – сжимающая, то для люб. x₀, x₁ из отрезка [a;b] должно происходить уменьшение длины (x₁ – x₀) при каждом новом отображении ф-и (x). Запишем условие сжатия след. образом:

В ф-ле сжимающегося отобр-я x<1 отсюда если вып. M/m*|x₁-x₀|<1, то метод сходится. |x^k+1-x^*|  M / m |x^k-x^*|²

ВОПРОС №6. Метод Стеффенсена. Условие сходимости. Геометрическая интерполяция.

Метод Стеффенса. В формулу метода Ньютона сделаем замену f  (x )  f(z ⁿ ) - f(x ⁿ )/ z ⁿ - x ⁿ при условии z ⁿ  x ⁿ и следует из определения производной f  (x ) = lim z x f(z)-f(x)/z-x.

Заменив z ⁿ = x ⁿ + f(x ⁿ ), x ⁽ⁿ⁺¹⁾ = x ⁿ - f²(x ⁿ )/ f(x ⁿ + f(x ⁿ ))- f(x ⁿ ), n  0.

Геометрическая иллюстрация.

Приближение x ⁿ получается как абсцисса т. пересечения с 0 x секущей, проходящей через т. М ⁿ и N ⁿ c координатами (x ⁿ , f(x ⁿ)) и (z ⁿ , f(z ⁿ )).Значение z ⁿ соответствует абсциссе т. пересечения с осью 0x прямой y = f(x ⁿ ) – (x - x ⁿ ), проходящей через т. Мⁿ и параллельной прямой y = - x.

ВОПРОС №7. Методы решения СЛАУ. Прямые и итерационные методы. Условие сходимости итерационных методов.

Численные методы линейной алгебры. К численным методам линейной алгебры относятся численные методы решения систем линейных алгебраических уравнений, обращения матриц, вычисления определителей и нахождения собственных значений и собственных векторов матриц.

Методы решения систем ЛАУ разбиваются на две группы. К первой группе точные или прямые методы – алгоритмы, позволяющие получить решение системы за конечное число арифметических действий. К этой группе относится метод Гаусса.

Вторую группу составляют приближенные методы (итерационные) решения СЛАУ.

Метод Гаусса Предназначен для решения СЛАУ вида:

или Ах=в

, ,

Предположим, что матрица А - невырожденная, т.е. det А не равно 0. В этом случае решение системы существует и оно единственно, а рассматриваемая задача корректна.

Вычисления с помощью метода Гаусса. Состоят из двух шагов, называемых прямым и обратным ходом. Прямой ход метода Гаусса заключается в последовательном исключении неизвестных из системы с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода. Рассмотрим простейший вариант метода Гаусса, называемый схемой единственного деления. Прямой ход состоит из (n-1) шагов исключения.

1-й шаг. Целью этого шага является исключение неизвестного x₁ из уравнений с номерами i = 2,3,...,n. Предположим, что коэффициент a₁₁  0 (главный элемент первого шага)

Вычислим величины _i1=a_i1 /a₁₁(i=2,3,...,n), называемые множителями 1-го шага. Вычтем из второго, третьего и ... до n-го уравнений системы (1) первое уравнение, умноженное соответственно на  ₂₁,₃₁,..., _n1.Это позволит обратить в нуль коэффициенты при х₁ во всех уравнениях , кроме первого. В результате получим эквивалентную систему.

в которой a_ij⁽¹⁾=a_ij-_i1 a_ij , b_i⁽¹⁾=b_i-_i1 b₁.

2-й шаг. На этом шаге производится исключение х₂ из уравнений с номерами i = 3, 4, . . . , n.

Вычислим _i2=a_i2⁽¹⁾/ a₂₂⁽¹⁾ относительно главного элемента 2-го шага, после чего произведем те же действия по исключению элементов а_i2 из 3-й n . . . строк.

Аналогично проводятся остальные шаги.

k-й шаг. Предположим, что главный элемент k-го шага a_kk^(k-1)0, вычислим множители k-го шага _ik= a_ik^(k-1)/a_kk^(k-1) , (i=k+1,...,n) и вычтем последовательно из (k + 1)-го , . . . , n-го уравнений полученной на предыдущем шаге системы k-е уравнение, умноженные соответственно на  _k+1,_k+2,..., _nk.

После (n -1) - го шага исключения получим систему уравнений

(2)

Получается матрица А^(n-1), которая является верхней треугольной. На этом вычисления прямого хода заканчиваются.

Обратный ход. Из последнего уравнения системы (2) вычислим х_n. Подставляя полученное значение в предпоследнее уравнение, вычислим значение х_n-1. Таким образом, можно вычислить значения всех неизвестных. Вычисления здесь проводятся по формулам:

Метод простой итерации.

Для того чтобы применить метод простой итерации к решению системы ЛАУ

Aх = b (3)

С квадратной невырожденной матрицей А, необходимо преобразовать эту систему к виду

х = Вх + с, (4)

где В - квадратная матрица с элементом b_ij (i,j=1.n), с - вектор столбец с элементами c_i (i=1,n).

Зададим некоторое начальное приближение x⁽⁰⁾=(x₁⁽⁰⁾,x₂⁽⁰⁾,..., x_n⁽⁰⁾)^T. Подставив его в правую часть системы (4), находим первое приближение x₍₁₎= Bx₍₀₎+c и так далее.

Сходимость метода простой итерации.

||B||<1. В этом случае существует и единственное решение системы (3) x. При этом метод итерации сходится при произвольном начальном приближении x⁽⁰⁾.

||B|| - норма матрицы.

Евклидова норма матрицы, имеет вид:

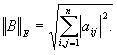
Критерий окончания итерационного процесса.

||x⁽ⁿ⁾-x^(n-1)|| < 

Метод Зейделя.

Пусть система (3) приведена к виду:

С коэффициентами, вычисленными по формулам:

в_ij = - a_ij / a_ii , c_ij = в_i / a_ii (i,j = 1,n , j i)

Метод Зейделя представляет собой модификацию метода простых итераций. Идея метода состоит в том, что при вычислении на (k+1)-ом шаге приближения к неизвестному х_i при i>1, используется уже найденное (k+1)-е приближение x ₁ , x ₂, . . . , x _i-1

Таким образом матрица В разбивается на две треугольные матрицы: верхнюю и нижнюю.

Расчетная формула принимает вид:

x ^k+1 =B₁ x ^k+1 + x ^k + C

или

Условия сходимости и критерий окончания итерационного процесса те же.

ВОПРОС №8. Метод простой итерации для решения СНУ. Теорема о сходимости методов.

Методы решения систем нелинейных уравнений.

f₁ (x₁, x₂, . . . , x_n) =0,

f₂ (x₁, x₂, . . . , x_n) =0,

..........

f_n (x₁, x₂, . . . , x_n) =0,

Найти точное решение системы (1), то есть вектор x = (x₁, x₂, . . . , x_n)^T удовлетворяющий уравнениям (1), практически невозможно, так как в описанном случае исключается использование прямых методов. Реальным путем решения системы (1) является использование итерационных методов для получения приближенного решения x^* = (x₁^*, x₂^* , . . . , x_n^*) удовлетворяющего при заданном  > 0 неравенству ||x^* - x|| < .

Для удобства будем использовать сокращенную векторную форму записи систем: вектор неизвестных x = (x₁, x₂, . . . , x_n)^T и векторную функцию f = (f₁, f₂, . . . , f_n)^T.

В этих обозначениях система (1) примет вид:

f (x) = 0. (2)